对《机器学习》的一些个人笔记与思考（7）

主要是对于周志华老师的《机器学习》一书（即西瓜书）以及吴恩达老师的关于《机器学习》的视频的一些笔记与思考。

第三章：线性模型

对于线性模型呢，我们是想能够把个样本点，通过线性组合建立起一个能够进行预测的函数，即

       

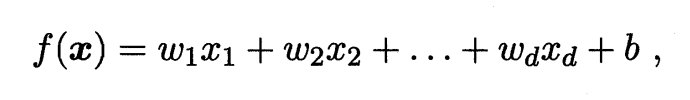
一般用向量形式写成：

（后面很常用的）

虽然线性模型看着简单，易于建模，但却蕴涵着机器学习中一些重要的基本思想。后续的算法很多也是从线性模型出发，对线性模型进行一个高维的映射或者引入层级的结构，从而衍生出各类算法。

下面我们就开始介绍一些比较经典的线性模型。

1.线性回归

对于给定数据集D={(x1​,y1​),(x2​,y2​),…,(xm​,ym​)}，“线性回归”试图学得一个线性模型以尽可能准确地预测实值输出标记。

这时候我们就需要将非数值的量，转化成数值量，以便输入线性模型

如何转变呢？比如：

(a) 有序属性

定义：属性值之间存在明确的顺序关系，如“高 > 中 > 低”。
处理方法：

• 二值属性（如“高/矮”）：
  直接映射为连续值，如：

  高→1.0,矮→0.0

• 三值属性（如“高/中/低”）：
  按顺序分配递减的数值，如：

  高→1.0,中→0.5,低→0.0

意义：保持属性值的顺序关系，使模型能捕捉到“高 > 中 > 低”的潜在趋势。

(b) 无序属性

定义：属性值之间无顺序关系，如“西瓜/南瓜/黄瓜”。
处理方法：

• 每个类别对应一个独立的二进制向量，例如：

  
  ​西瓜→(1,0,0)
• 南瓜→(0,1,0)
• 黄瓜→(0,0,1)​

这样就可以完成转化了。

回归正题，即线性回归试图习得：

方向有了，如何得到w和b呢？这时候就得请出我们之前在性能度量提到的“均方误差”了

因为需要尽可能准确，所以我们当然希望均方误差越小越好，所以我们就去求均方误差的最小值

即：

通过使用均方误差求最小值以得到线性模型的方法也叫做“最小二乘法”。即找到一条直线，使得所有样本到直线的欧氏距离之和最小。

注：有关欧氏距离：欧氏距离是一个通常采用的距离定义，它是在n维空间中两个点之间的真实距离，n维空间中，A，B两点欧式距离为d(AB) =sqrt [ ∑( ( a - b )^2 ) ] (i = 1，2…n)

求解w和b使最小化的过程，称为线性回归模型的最小二乘“参数估计”。

因为要求最小值，我们自然而然地想到了求导，没错！我们就对w和b求导化简

推导过程如下：

以及：

同时令上述两式为0时，即可得到w和b的解：

这样我们就求出了w和b了