《电子技术基础（数字部分）》第 2 章逻辑代数 & 硬件描述语言基础-CSDN博客

逻辑代数是1854年问世的，最早用于开关和继电器网络的分析及化简，随着半导体器件制造工艺的发展，各种性能良好的微电子开关器件不断涌现，逻辑代数成为分析和设计逻辑电路不可缺少的数学工具。利用这种数学工具，可以把逻辑电路输入和输出之间的关系用代数方程表示出来。
逻辑代数有一系列的定律、定理和规则，用它们对数学表达式进行处理，可以完成对逻辑电路的化简、变换、分析和设计。

2.1.1 逻辑代数的基本定律和恒等式

表2.1.1列出了常用的逻辑代数基本定律和恒等式。等式中的字母(例如A、B、C)为逻辑变量，其值可以取0或1，代表逻辑信号的两种可能状态之一。

表2.1.1中除了还原律和最后一组恒等式外，其他基本定律或恒等式是成对出现的，具有对偶性。为了进一步简化表达式的形式，在不产生混淆的前提下，可以省略与运算符“·”。

在以上所有定律中，数学家摩根提出的反演律具有特殊重要的意义。反演律又称为摩根定理，它经常用于求个原函数的非函数或者对逻辑函数进行变换。

用完全归纳法可以证明表2.1.1所列等式的正确性，方法是：分别列出等式左边表达式与右边表达式的真值表，如果等式两边的真值表相同，说明等式成立。

也可以从集合论的角度去理解。

上面这些基本定理对化简逻辑函数表达式十分有用，也就是说，可以用来减少表达式中乘积项的数量。

注意，本节列出的基本定律和恒等式反映了逻辑关系，而不是数量之间的关系，在运算中不能简单套用初等代数的运算规则。如初等代数中的移项规则就不能用，这是因为逻辑代数中没有减法的缘故。

2.1.2 逻辑代数的基本规则或定理

（1）代入规则

代入规则：在任何一个逻辑等式中，如果用一个函数代替等式两边出现的某变量A，则等式依然成立，这个规则称为代入规则。

代入规则可以扩展所有基本公式或定律的应用范围。

（我的理解：A—>f(A,B,C,D,E,F……)，作用之一：实现双变量定律/定理/规则到多变量的推广）

（2）反演规则

反演规则：根据摩根定理，由原函数L的表达式，求它的非函数L时，可以将L中的与(·)换成或( + )，或(+)换成与(·)；再将原变量换为非变量(如A换成~A)，非变量换为原变量；并将1换成0，0换成1；那么所得的逻辑函数式就是~L。

利用反演规则，可以比较容易求出一个原函数的非函数。运用反演规则时必须注意以下两个原则：

(1）保持原来的运算优先级，即先进行与运算，后进行或运算。并注意优先考虑括号内的运算。

(2)对于非变量以外的非号应保留不变。

（3）对偶规则

设L是一个逻辑表达式，若把L中的“与、或互换，0、1互换”，那么就得到一个新的逻辑函数式，这就是L的对偶式；记作L'。

与、或互换就是把与(·)换成或(+)，或(+)换成与(·)；0、1互换就是把1换成0，0换成1。变换时需注意保持原式中“先括号、然后与、最后或”的运算顺序。

对偶规则：当某个逻辑表达式相等，则它们的对偶式也相等。

对偶性意味着逻辑代数中每个逻辑恒等式可以用两种不同的表达式进行表示。即任何一个定理的对偶表达式也是正确的。

注意，对偶变换时，逻辑变量本身（原非）、逻辑变量位置、逻辑变量相互间的运算顺序均保持不变。

例：A+~A·B = A+B成立，则A·(~A+B) = AB也成立。

（4）香农展开定理

2.2 逻辑函数表达式的形式

任何一个逻辑函数，其表达式的形式都不是唯一的。

2.2.1 逻辑函数表达式的基本形式

（1）与-或表达式

与-或表达式：对若干与项进行或运算——变量先与完，与项再整体参与或运算。

与项(或乘积项)：由与(逻辑乘)运算把变量连接起来的式子。

与-或式：将若干个与项用或运算符连接起来，称这种类型的表达式为与-或式，或称之为“积之和 ( sum of products , SOP)”表达式。

注意：单变量D可以认为是与项D·1、或项(D+1)

（2）或-与表达式

或-与表达式：由若干或项进行与逻辑运算构成的表达式。

或项：由或(逻辑加)运算符把变量连接起来的式子。

或-与式：将若干个或项用与运算符连接起来称这种类型的表达式为或-与式，或称之为“和之积( products of sum, POS)”表达式。

逻辑函数式通常表示成混合形式——既不是与-或式，也不是或-与式。

但经过变换可以转化成上述两种基本形式。

2.2.2 最小项与最小项表达式

（1）最小项的定义和性质

最小项：对于有n个变量的逻辑函数，若有一个乘积项（与项）包含了全部的n个变量，每个变量都以它的原变量或非变量的形式在乘积项中出现，且仅出现一次，则称该乘积项为最小项。

结论：一般n个变量的最小项应有2^n个。

最小项编号：最小项通常用mi表示，下标i即最小项编号，用十进制数表示。将最小项中的原变量用1表示，非变量用0表示，二进制—>十进制，可得到最小项的编号。

三个变量A、B、C的全部8个最小项及其最小项的代表符号如表2.2.1所示。

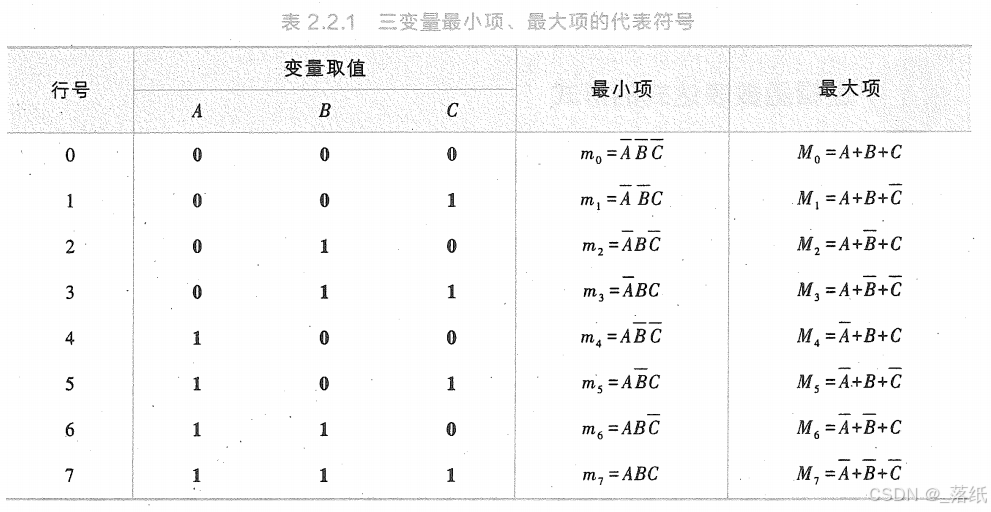
观察表2.2.2可以看出，最小项具有下列性质。

① 任意一个最小项，输入变量只有一组取值使其值为1，而其他各组取值均使其为0。

并且，任意一组输入变量取值，有且只有一个最小项为1，而其他最小项为0

② 任意两个不同的最小项之积为0。

③ 所有最小项之和为1。

（集合论：完备事件组）

（2）最小项表达式

由若干最小项相或构成的逻辑表达式称为最小项表达式，也称为标准与-或表达式。

最小项表达式的简便表示：编号表示——eg：L=m1+m3+m6

逻辑表达式一般形式——>最小项表达式：

结论：任意一个逻辑函数都能变换成唯一一个最小项表达式。

2.2.3 最大项与最大项表达式

（1）最大项的定义和性质

最大项：对于有n个变量的函数来说，若有一个或项包含了全部的n个变量，每个变量都以它原变量或者非变量的形式在或项中出现，且仅出现一次，则称该或项为最大项。

由若干最大项组成的或式，称为标准或-与表达式。

结论：一般n个变量的最大项应有2^n个。

最大项编号：最大项通常用Mi表示，下标编号i用于区别不同的最大项。对于一个最大项，输入变量只有一组二进制数使其取值为0，与该二进制数对应的十进制数就是该最大项的下标编号。

三个变量A、B、C的全部8个最大项及其最大项的代表符号如表2.2.1所示。表中每行列出的二进制数都使与其对应的最大项的值为0。

根据最大项的定义，得到最大项具有下列性质：

① 任意一个最大项，输入变量只有一组取值使得它的值为0，而在变量取其他各组值时，这个最大项的值都是1。并且，最大项不同，使其值为0的输入变量取值也不同。

② 任意两个不同的最大项之和为1。

③ 所有最大项之积为0。

（2）最小项与最大项的关系

根据最小项和最大项的性质可知，相同变量构成的最小项与最大项之间存在互补关系，即

结论：任一个逻辑函数经过变换，都能表示成唯一的最大项。

2.3 逻辑函数的代数化简法

在设计逻辑电路时，根据实际要求直接归纳出来的逻辑函数式往往不是最简的形式，这就需要对逻辑函数式进行化简。

化简的目的：为了降低电路实现的成本，以较少的门实现电路。

显然，简化电路使用较少的门，比原来电路的体积小且成本低。简化电路的连线较少，减少了电路可能潜在的故障，可靠性得到进一步的改善。

简化逻辑函数的方法很多，本节将介绍代数化简法，下一节介绍卡诺图法。

一个逻辑函数可以有多种不同的逻辑表达式，如与-或表达式，与非-与非表达式、或-与表达式、或非-或非表达式、与-或-非表达式等。

通常与-或表达式易于转换为其他类型的函数式，所以下面着重讨论与-或表达式的化简。

最简与-或表达式：在若干个具有相同逻辑关系的与-或表达式中，将其中包含的乘积项个数最少，且每个乘积项中变量数最少的表达式称为最简与-或表达式。

逻辑函数化简就是要消去与-或表达式中多余的乘积项和每个乘积项中多余的变量，以得到逻辑函数的最简与-或表达式。

有了最简与-或表达式以后,再用公式变换就可以得到其他类型的函数式。

2.3.1 逻辑函数的化简

代数法是运用逻辑代数中的定理、恒等式或规则对逻辑函数进行化简，这种方法需要一些技巧，没有固定的步骤。下面是经常使用的方法。

（1）并项法

（2）吸收法

（3）消去法

（4）配项法

2.3.2 逻辑函数形式的变换

逻辑函数的化简的目的：逻辑函数的形式的最间

逻辑函数的形式变换的目的：逻辑图的最简（使用的门电路种类最少）

可能逻辑函数的表达式不是最简的（逻辑项数最少），但是用了同一种门电路，那么做电路板的时候就很方便，只需要使用同一种门电路，这也是一种优化的思想——通常在一片集成电路芯片中只有一种门电路，通常是4个、8个同一种门电路，可能最简逻辑函数表达式需要用到很少门电路，但是种类不少，反而需要多块不同芯片，不够简便。

为了减少门电路的种类，需要对逻辑函数表达式进行变换。

① 与-或——>与非-与非

首先对与-或表达式取两次非，然后按照摩根定理分开下面的非号。

实际的集成电路（门电路）例如74LS00——最典型、最常用的一种门电路芯片，一片里面有4个单元，每个单元是一个二输入的与非门，如果没有把一片里面的4个单元全部用完，要用其他种类的门电路，用与门、或门、非门就需要使用3片集成的门电路，就很浪费。

全部使用与非门，就能只用一种芯片。对于实际生产备料也很有好处，只用备一种料。

（注：非变量可以用与非门得到——自己和自己与非、自己和1（上拉电平）与非）

② 与-或——>或非-或非

首先对与-或表达式中的每个乘积项单独取两次非，然后按照摩根定理分开下面的非号。

2.4 逻辑函数的卡诺图化简法

利用代数法可使逻辑函数变成较简单的形式，但经代数法化简得到的逻辑表达式是否为最简式较难判断。

卡诺图法：程序性很强，按步骤走一般都能得到最简式。

2.4.1 用卡诺图表示逻辑函数

（1）卡诺图的引出

卡诺图：将n变量的逻辑函数的全部最小项都用小方块表示，并使具有逻辑相邻的最小项在几何位置上也相邻地排列起来，这样，所得到的图形叫n变量的卡诺图。

（逻辑相邻——>几何相邻）

逻辑相邻的最小项：如果两个最小项只有一个变量互为反变量，那么，就称这两个最小项在逻辑上相邻。

① 一变量卡诺图

对于n个变量的逻辑函数有2^n个最小项，因此一变量的逻辑函数有2个最小项。设变量为D，则其两个最小项是D和~D，分别记为m0=~D，m1=D。

用两个相邻的方格表示这两个最小项，如图2.4.1(a)所示。方格上的~D和D分别表示非变量和原变量。为简明起见，非变量D可以不标出，只标出原变量D,得到图2.4.1( b)。图2.4.1( c)是另一种更简单的画法，图中m0、m1只用其下标编号来表示。

② 二变量卡诺图

二变量逻辑函数的最小项有4项，如果逻辑函数的变量用C，D表示，则m0=~C~D，m1=~CD，m2 = C~D，m3=CD。用四个相邻的方格来表示这四个最小项。

将一变量卡诺图按照图2.4.2( a)所示箭头方向展开，得到二变量卡诺图如图2.4.2(b)所示。新增加的两个方格标以变量C，新方格最小项的编号相对原方格编号增加了2^(n-1)=2，即方格0后面为方格2，方格1后面为方格3。按照展开规律，中间两格m1和 m3包含原变量D，右边两方格m3和m2包含原变量C，图中清楚地展示了原变量所包含的方格。

综上所述，可归纳“折叠展开”的法则如下：

Ⅰ新增加的方格按展开方向应标以新变量；
Ⅱ新方格内最小项编号应为展开前对应方格编号加上2^(n-1)。

按照同样的方法，从二变量卡诺图展开获得三变量卡诺图，如图2.4.3所示。三变量逻辑函数L(B,C,D)有8个最小项，可用8个相邻的方格来表示。新增加的四个方格标以变量B，并且其最小项编号相对原方格的编号加上2^(n-1)= 4。方格所处的位置，与相应的最小项对应，例如，2号方格处于变量为~B、C、~D的区域，则m2=~BC~D，余类推。

同理，可得四变量卡诺图，如图2.4.4所示。在使用时，根据方格所在区域对应的变量A、B、C、D的取值，可直接填入相应的最小项。

（2）卡诺图的特点

卡诺图的特点：各小方格对应于各变量的不同组合，几何位置相邻的方格（最小项）在逻辑上也是相邻的（只有一个因子差异）。即相邻的两个方格（最小项）只有一个变量不同，这是用卡诺图化简逻辑函数的主要依据。

要特别指出的是：卡诺图同一行最左端和最右端的方格是相邻的，同一列最上端和最下端两个方格也是相邻的。

这个特点说明在几何位置上卡诺图具有上下、左右封闭的特性。

由于卡诺图具有相邻方格仅一个变量不同的特点，所以相邻方格二进制编号也只有一位不同——所以第一行是0、1、3、2，第二行是……

（3）卡诺图的简化表示法

图2.4.6所示为图2.4.5所示的卡诺图简化形式。变量A、B、C、D的每组取值，与对应方格内的最小项编号一一对应。

（4）已知逻辑函数，画出卡诺图

当逻辑函数为最小项表达式时，在卡诺图对应最小项的方格填上1，其余的方格填上0(也可用空格表示)，就可以得到相应的卡诺图。

也就是说，任何逻辑函数都等于其卡诺图中为1的方格所对应的最小项之和。

当逻辑函数的表达式为其他形式时，可将其变换为最小项表达式后，再作出卡诺图。

2.4.2 用卡诺图化简逻辑函数

（1）化简的依据

卡诺图具有相邻性：

若两个相邻的方格均为1，则这两个最小项之和有一个变量可以被消去。

若四个相邻的方格均为1，则这四个最小项之和有两个变量可以被消去。

若八个相邻的方格均为1，则这八个最小项之和有三个变量可以被消去。

……

（2）化简的步骤

用卡诺图化简逻辑函数的步骤如下：

① 将逻辑函数写成最小项表达式。

② 按最小项表达式填卡诺图。

③ 找出为1的相邻最小项，用虚线(或者细实线)画一个包围圈，每个包围圈含2^n个方格，写出每个包围圈的乘积项。

④ 将所有包围圈对应的乘积项相加。

有时也可以由真值表直接填卡诺图，以上的①②两步就合为一步。

画包围圈的原则：

① 包围圈内的方格数必定是2^n个，n等于0、1、2、3、…。

② 相邻方格包括上下底相邻，左右边相邻和四个角两两相邻。

③ 同一方格可以被不同的包围圈重复包围，但新增包围圈中一定要有新的方格，否则该包围圈为多余。

④ 包围圈内的方格数要尽可能多，包围圈的数目要尽可能少。

化简逻辑函数后，一个包围圈对应一个乘积项，包围圈越大，所得乘积项中的变量越少。包围圈个数越少，乘积项个数也越少，得到的与-或表达式也最简。

（3）具有无关项的化简

在实际工作中，当逻辑变量被赋予特定含义时，有些变量的取值组合是不应该出现的，这些变量取值组合对应的最小项称为约束项。例如,在8421BCD码中,，010~1111这六种组合是不使用的代码(应该被限制)，在输入端不应该出现，因此，这六种组合对应的最小项为约束项。

而在有的情况下，受客观条件所限，有些最小项根本不会出现。

某些取值组合客观上是不会出现的，于是其函数值可以是任意的(它的值可以取0或取1)，将变量取这些值所对应的最小项称为任意项。

约束项和任意项统称为无关项。合理利用无关项，可以使逻辑函数得到进一步简化。无关项的值可以取0或取1，具体取什么值，应该以得到的逻辑函数式最简为准。

用m表示最小项类似，用d表示无关项，其对应的函数值通常以×(或Φ)表示。

2.5 硬件描述语言Verilog HDL基础

硬件描述语言(HDL)类似于计算机高级程序设计语言(如C语言等)。

它是一种以文本形式来描述数字系统硬件结构和功能的语言。

用它可以表示逻辑电路图、逻辑表达式，还可以表示更复杂的数字逻辑系统所完成的逻辑功能(即行为)。人们还可以用 HDL编写设计说明文档，这种文档易于存储和修改，适用于不同的设计人员之间进行技术交流，还能被计算机识别和处理。

HDL是高层次自动化设计的起点和基础。

计算机对 HDL的处理包括两个方面：逻辑仿真和逻辑综合。

逻辑仿真：指用计算机仿真软件对数字逻辑电路的结构和行为进行预测，仿真器对HDL描述进行解释，以文本形式或时序波形图形式给出电路的输出。

在电路被实现之前，设计人员根据仿真结果可以初步判断电路的逻辑功能是否正确。在仿真期间，如果发现设计中存在的错误，可以直接在软件层面对HDL描述进行修改，直至满足设计要求为止，而不用涉及硬件修改。

逻辑综合：指将HDL 描述的电路的逻辑关系，转换为门和触发器等元件列表 & 其相互之间的连接关系表(常称为门级网表)的过程，即将 HDL代码转换成真实的硬件电路。

它类似于高级程序设计语言中对一个程序进行编译，得到目标代码的过程。所不同的是，逻辑综合不会产生目标代码，而是产生门级元件及其连接关系的数据库；根据这个数据库可以制作出集成电路或印制电路板( printed circuit board , PCB)。

目前，Verilog HDL(简称Verilog)和VHDL 在数字设计领域的使用非常广泛，它们都已经被IEEE认可为工业标准。尽管这两种语言在很多方面都有所不同，但在学习逻辑电路时，设计者使用任何一种语言都可以完成自己的任务，并且Verilog的句法根源出自通用的C语言，较VHDL易学易用。作为入门，本书以Verilog为主讲解硬件描述语言的基本知识。

2.5.1 Verilog HDL模块的基本结构

模块(module)是Verilog描述电路的基本单元，它可以表示一个简单的门电路，也可以表示功能复杂的数字电路。

对数字电路建模时可以使用一个或多个模块进行描述(也称为建模)，不同的模块之间通过端口进行连接。

定义模块时总是以关键词module开始，并以关键词endmodule结束。模块的组成如图2.5.1所示：

（关键词是verilog本身规定的特殊字符串，用于表示特定的含义）

module后面紧跟着“模块名”，模块名是模块唯一的标识符；在模块名后面的圆括号中列出该模块的输入、输出端口名称，各个端口名称之间以逗号分隔。

在 Verilog 中，通常以input(输入) , output(输出)、 inout(双向端口)来说明信号流经端口的方向；

“参数定义”是将数值常量用符号常量代替，以增加程序的可读性和可修改性，它是一个可选择的语句。

“数据类型定义”部分用来指定模块内所用的数据对象为连线( wire)类型还是寄存器(reg)类型。

接着，描述模块将要完成的逻辑功能。通常有三种不同的描述风格：

一是实例引用低层次模块的方法，即调用其他已定义过的层次较低的子模块对整个电路的结构进行描述，或者直接调用Verilog内部预先定义的基本门级元件描述电路的结构，通常将这种方法称为结构描述方式(对仅使用基本门级元件描述电路功能的方式，也称为门级描述方式)；

二是使用连续赋值语句( assign)对电路的逻辑功能进行描述,通常称之为数据流描述方式，该方式特别便于对组合逻辑电路建模；

三是使用过程块语句结构(包括initial结构和 always结构两种)和比较抽象的高级程序语句对电路的逻辑功能进行描述，通常称之为行为描述方式。行为描述侧重于模块的逻辑功能，不涉及实现该模块的详细硬件电路结构。

设计人员可以选用这三种方式中的任意一种或混合使用几种方式对电路的功能进行描述，并且这几种描述方式在程序中排列的先后顺序是任意的。这些描述方式将在4.6节、5.6节和6.7节做进一步介绍。除此之外，在3.8节中还介绍了开关级描述方式。

下面使用两种不同的描述方式对该电路建模。图2.5.3是Verilog的门级描述方式，而图·2.5.4则是数据流的描述方式。

在Verilog设计中，使用文件的方式来保存模块的描述，文件的扩展名为* .v，图2.5.3和图2.5.4中代码的第1行均给出了文件名。双斜线“//”后面是注释，到本行结尾处，注释结束。

图2.5.3是根据图2.5.2所示的电路图进行描述的。首先描述了电路的输人、输出端口，以及电路内部的节点信号，接着描述了电路的结构(即逻辑功能)，这里直接调用Verilog语言内部预先定义的基本门级元件( not、 and , or )来描述逻辑图中的元件以及元件之间的连线关系。在每个逻辑门元件后面跟着一个实例名(U1,U2等)和由圆括号括起来、以逗号分隔的电路端口；

Verilog 规定：输出端口总是位于圆括号内左边第1个位置，输入端口跟在后面。例如，对于实例名为U4的或门，其输出端口是Y、输入端口是A和B，实例名可以直接使用，不需要预先定义。实际上，调用基本门级元件时，实例名可以省略不写。

每一条语句以分号结尾，但模块最后的endmodue后面没有分号。由于这个模块是用来描述电路逻辑功能的，故将该模块称为设计块。

图2.5.4的代码采用了数据流描述方式。这里，模块的声明如下：

module mux2to1_df( input DO, D1 ,S, output wire Y);

这是修订版本Verilog-2001/2005标准的写法。在模块的端口列表中，直接声明端口方向，不再需要独立的 input和output语句，这使代码变得更加紧凑。本书后面的代码将采用这种方式。

电路功能是根据前面推导出来的逻辑表达式描述的。由关键词assign 开始，后面跟着由操作数和运算符(类似于C语言中的运算符)组成的逻辑表达式。使用逻辑表达式编写Verilog代码，具有简明、易懂的优点。将图2.5.4的代码送到逻辑综合软件进行综合，得到如图2.5.5所示的逻辑图，它与图2.5.2所示的门级电路完成的功能相同。

2.5.2 逻辑功能的仿真与测试

一旦完成了设计块后，接下来就要测试这个设计块描述的逻辑功能是否正确。为此必须在输入端口加入测试信号，以便检测输出端口的结果是否正确，这一过程常称为搭建测试平台( test bench)。

根据仿真软件的不同，搭建测试平台的方法也不同，下面以 ModelSim 软件为例进行说明。

在对一个设计块进行仿真时，需要准备一个测试模块。

该模块大致由三部分组成：

第一部分实例引用被测试的模块(即设计块)。

第二部分是给输入信号赋各种不同的组合值，即激励信号。

第三部分指定测试结果的显示格式，并指定输出文件名。

由于测试模块的主要任务是给设计块提供激励信号，所以也称为激励块。

激励块通常是顶层模块，同样用Verilog HDL来描述。它是以module开始并以 end-module结尾的，内部包括模块名、数据类型的声明、低层次模块的实例引用和行为语句块( initial或者always)，但是不需要声明端口。

在激励块中，通常会使用编译指令`timescale将时间单位与实际时间进行关联。编译指令( compiler directives)为仿真工具提供有关如何解释Verilog 模型的附加信息。编译指令放在模块定义之前，并以反引号(即`)开头。`timescale的格式为：

`timescale time_unit/time_precision

其中，time_unit为仿真时间单位，time _precision为仿真时间的精度(即最小分辨度)。注意，时间单位通常大于或等于时间精度。

图2.5.6是2选1数据选择器激励块代码，文件名为test_mux2to1_df.v。第1条语句用`timescale将激励块中所有延迟时间的单位设置成1 ns ，模块后面的5代表延迟5 ns。

接着，声明激励块的名称为test_mux2to1_df。在激励块中，可以重新定义一套信号端口名称，也可以与设计块中的端口名相同，但输入信号的数据类型要求为reg，以便保持激励值不变，直至执行到下一条激励语句为止。输出信号的数据类型要求为 wire，以便能随时跟踪激励信号的变化。
接下来，实例引用(调用)设计块，按照端口排列顺序一一对应地将激励块中的信号端口与设计块中的端口相连接，在本例中，将PD0、PD1、PS、PY分别对应地连接到设计块mux2to1_df 中的端口D0、D1、S、Y。

initial语句下面的过程赋值语句给出了激励信号的输入值。仿真时，刚进人initial的时刻为0，此时执行语句1，将 PS、PD1 和 PD0的值初始化为0，隔5 ns后，执行语句2，将PD0的值设置为1，PS、PD1的值仍保持0不变；再隔5 ns ,执行语句3，将 PD0的值设置为0，将PD1的值设置为1，PS 的值仍保持0不变……语句10执行后，initial语句永远被挂起。

最后面的initial语句描述了要监视的输出信号，它和前面的 initial语句是同时并行执行的。代码中的$monitor 、$ time和 $stop 为Verilog HDL 的系统任务，$monitor将信息以指定的格式输出到屏幂上，双引号括起来的是要显示的内容，%b代表它后面的信号用二进制格式显示，\t代表水平制表符，$time将返回当前的仿真时间，$stop为停止仿真，但不退出仿真环境。常用的系统任务和编译指令将在附录C中介绍。

对例2.5.1进行仿真时，打开任意一个文本编辑器(或者使用ModelSim 软件自带的编辑器)，输入设计块和激励块源文件，并存放在一个新建的子目录中。然后，在 ModelSim 软件创建一个新的工程项目，添加已经存在的源文件（mux2to1_df.v和test_mux2to1_df.v），并编译，最后进行逻辑功能仿真，得到图2.5.7所示的波形。同时，在ModelSim f的transcript窗口以文本方式显示的结果如图2.5.8所示。注意，如果激励模块中没有$monitor语句，仿真结果中就只有波形图，而不会出现图2.5.8所示的结果。

由图2.5.7可知，在0~20 ns期间，由于PS=0，所以输出PY与输入PD0相同；在20~40 ns 期间， PS=1，故输出PY与输入PD1相同。表明该设计块描述的逻辑功能是正确的。

对一个实际的门电路来说，信号从输入端传到输出端存在着延时，在使用Verilog 建模时，有时需要说明门电路的延时，有关内容可以阅读专门书籍。

2.5.3 Verilog HDL的基本语法规则

要用Verilog对逻辑电路建模，必须了解Verilog语言的基本语法规则。下面进行简单介绍。

（1）间隔符

Verilog 的间隔符包括空格符(\b)、TAB键(\t)、换行符(\n)及换页符。

间隔符主要起到分隔文本的作用，可以使文本错落有致，便于阅读和修改。

如果间隔符并非出现在字符串中，则该间隔符被忽略。所以编写程序时，可以跨越多行书写，也可以在一行内书写。

（2）注释符

Verilog 支持两种形式的注释符：

/*--------*/：可用于多行注释。

//----------：单行注释符，从双斜线//开始到行尾结束。

注释只是为了改善程序的可读性，在编释时不起作用。

（3）标识符和关键词

标识符：给对象(如模块名、电路的输入与输出端口、变量等)取名所用的字符串称为标识符。

标识符(Identifier)通常是由英文字母、数字、$符或者下划线组成的字符序列，但标识符的第一个字符必须是英文字母或者下划线。此外，标识符是区分大、小写英文字母的。

关键词：Verilog本身规定的特殊字符串，通常为小写的英文字符串。不能作为标识符使用，在Verilog中有100个左右预定义的关键词。

例如：module、endmodule、input、output、wire、reg、and等都是关键词。

（4）逻辑值集合

为了表示数字逻辑电路的逻辑状态，Verilog 语言规定了4种基本的逻辑值(也被称为四值逻辑系统)，如表2.5.1所示。

（5）常量及其表示

Verilog中有两种类型的常量：整数型常量和实数型常量。
整数型常量有两种不同的表示方法：

① 使用简单的十进制数形式表示整数，例如：30、-2都是十进制数表示的整数。用这种方法表示的整数被认为是有符号的常量，负数可以使用补码形式表示。

② 使用带基数的形式表示整数，由4个部分组成，其格式为：

<+/-><size>'<signed>radix intefer_number

//尖括号<>内的内容表示非必要内容，可有可无

<+/->：表示常量是正整数还是负整数，当常量为正整数时，前面的正号可以省略；

<size>：表示常量对应二进制数的位数(位宽)；

<signed>：用小写s或大写S表示有符号的数；

radix：b或B（表示二进制数），d或D（表示十进制数）、o或O（表示八进制数）、h或H（表示十六进制数）。

integer_number：是基于基数( radix)格式的数值——数值中的x、z以及十六进制数的a~f是不区分大小写的。

下面是一些常数的示例：

4'b1x0x        4位的二进制数
8'he3          8位的十六进制数
8'b1001_0011   在数字之间可以增加下划线，以改善可读性

基数格式的数中如果没有s，则通常为无符号数。

另外，表示整数位宽的常数是可选的，如果没有定义位宽，则该数的位宽至少为32位。例如：

'hAF    32位十六进制数，无符号
'sb1011 32位二进制数，有符号的-5

若定义的位数较少，则数值最左边的多余位将被截断。若定义的位数多于数值所需要的位数时，对无符号数则在数值的左边填0补齐，而对有符号数则在左边填符号位补齐。但是如果数值的最左边一位为x或z，则相应地用x或z在左边补齐。例如：

3'sb10100     等同于3'sb100
10'bxOx1      左边补x,结果为xx__xxxx_x0x1
8'sb101101    左边补符号位(1),结果为1110_1101

实数型常量也有两种不同的表示方法：
(1）使用十进制数表示法。例如：0.1、2.0、5.67等都表示实数型常量。
(2）使用科学记数法。例如：23_5.1e2、3.6E2、5E-4等，它们以十进制数表示分别为23 510.0、360.0和0.0005。

（6）参数

Verilog允许用参数定义语句定义一个标识符来代表一个常量，称为符号常量，可以同时定义若干个参数。

参数是由一个标识符和一个常量组成的，参数经常用于指定延迟、变量的位宽等。参数声明语句的格式为:

parameter<signed><[mab:lsb]>参数名1=常量表达式1,参数名2=常量表达式2,…;

signed表示参数为有符号的数；

[ msb : lsb]用于指定参数值的范围。

下面是一些参数声明的示例:

parameter N = 4,Pi = 3.14,Byte = 8;
parameter S0= 2'b00,S1 =2'b01,S2=2'b10,S3=2'b11;    //声明4个无符号数值
parameter signed [ 3: 0] MEM_DR =-5,CPU_SPI=6;      //声明2个有符号的4位数值

标识符N在代码中可以用在表示数字4的地方，而S0可以用于替换数值2'b00，等等。

注意：使用参数声明语句只能对参数赋一次值。参数是局部的，仅在声明该参数的模块内部起作用。参数值可以在编译时被改变。可以使用defparam(即重新定义参数)语句来改变参数值,也可以通过在实例引用模块的语句中指定新的参数值而加以修改。

（7）字符串

字符串是双引号内的字符序列，不允许分成多行书写。在表达式和赋值语句中，字符串要转换成无符号整数，用一串8位ASCII值表示，每一个8位ASCII值代表一个字符。

例如：字符串“ab”等价于16'h6162。存储字符串“INTERNAL ERROR”，需要定义8x14位的变量。字符串中的特殊字符必须用转义字符“\”来说明。

2.5.4 数据类型

Verilog有两大类数据类型：一类是线网类型(net type) ，另一类是变量类型( variable type) 。

（注：在IEEE1364-2001标准公布之前，变量类型被称作寄存器类型-register type）

（1）线网类型

线网类型：是指输出始终根据输入的变化而更新其值的变量，它一般指的是硬件电路中的各种物理连接。

线网类型是硬件电路中元件之间实际连线的抽象。线网的值由驱动元件的值决定。如果没有驱动元件连接到线网，则线网的默认值为高阻态z(线网trireg除外，它的默认值为x)。

例如：图2.5.9所示线网L跟与门G1的输出相连，线网L的值由与门的驱动信号a和b所决定。

即L= a&b。a、b 的值发生变化，线网L的值会立即跟着变化。

线网类型有wire、wand、wor、tri、triand、trior、trireg 等多种。常用的线网类型由关键词wire进行声明，其格式如下:

wire<sigmed><[msb:isb]>net_namel , net_name2, … , net_nameN;

关键词signed是可选的，用signed声明的线网是有符号数(以2的补码形式保存)的线网；没有signed时表示无符号数的线网。

位宽[msb: lsb]：也是可选的，不指定位宽时，默认为1位宽的线网。

下面是一些例子：

wire a,b,L;                          //声明3个1位的线网(连线)
wire signed [7 : 0]usb_data;         //声明一个8位宽的线网,其数值为2的补码形式
wire [ 32 ∶ 1 ] busA , busB , busC; //声明3个位宽为32的线网

在Verilog模块中，如果没有明确定义输入、输出端口的数据类型，则默认为是1位宽的wire型。

下面是实例分析：

方框的输入、输出端口，圆圈是内部节点——线网

（2）变量类型

线网( wire)提供了一种逻辑元件之间相互连接的方式，但在行为描述方式中，却不能给线网赋值。为了实现这个目的，Verilog 提供了变量。

变量：表示一个抽象的数据存储单元——不对应具体硬件，它只能在 initial或always内部被赋值，在一条行为描述语句中给变量赋值后，这个值会保持不变，直到被再次赋值为止。

变量在没有被赋值前，它的默认值是x。

Verilog有5种不同的变量类型，如表2.5.2所示。

最常用的变量类型是用关键词reg声明的寄存器类型，其格式如下：

reg<signed><[msb : lsb]>reg_name1 , reg_name2 , … , reg...nameN ;

reg 型变量的值通常被解释为无符号数，但可以用signed声明它是有符号变量，此时reg保存的就是有符号数(以2的补码形式保存)。

位宽[ msb: lsb]也是可选的，如果没有指定位宽，则默认为是1位宽的reg 型变量。

下面是一些例子：

reg clock ;                        //声明一个无符号寄存器型变量
reg[ 3 : 0] counter;               //声明一个无符号的4位寄存器变量
reg signed [ 16∶ 1 ]sim_counter;  //sim_counter 以2的补码形式保存有符号数

在Verilog 中，常常将位宽为1的线网(例如 wire)或变量(例如reg)称为标量，而将位宽大于1的线网或变量称为向量( vector )。

integer、real、realtime和 time 等变量都是纯数学的抽象描述，不对应任何具体的硬件电路。integer型变量通常用于对整数型常量进行存储和运算，在算术运算中，integer型数据被视为有符号的数，用二进制补码的形式存储。而reg 型数据通常被当作无符号数来处理。注意integer型变量不能使用位向量，例如 integer[ 3 ∶ 0]num;的定义是错误的。

real和 realtime型变量完全相同，通常用它们对实数型常量进行存储和运算，实数不能定义位宽，其默认值为0。当实数值被赋给一个integer型变量时，只保留整数部分的值，小数点后面的值被截掉。
real型变量的应用举例如下：

real delta;            //声明一个实数型变量
initial
    begin
        delta = 4e10;  //给delta赋值
        delta = 2.13;
    end
integer i;             //声明一个整型变量
initial
    i = delta;         //i得到的值是2(只将实数2.13的整数部分赋给i)

time型变量主要用于存储仿真的时间，它只存储无符号数。每个time型变量存储一个至少64位的时间值。为了得到当前的仿真时间，常调用系统函数$time。

time型变量的应用举例如下:

time current__time ;        //声明一个时间类型的变量
initial
   current__time = $time    //保存当前的仿真时间到变量 current__time 中

2.5.5 运算符及其优先级

（1）运算符

数据流建模时，会用到运算符来描述逻辑函数表达式。表2.5.3列出了Verilog 语言提供的运算符及其符号。按照功能可以大致分为算术运算符、逻辑运算符、关系运算符、移位运算符等几大类。·

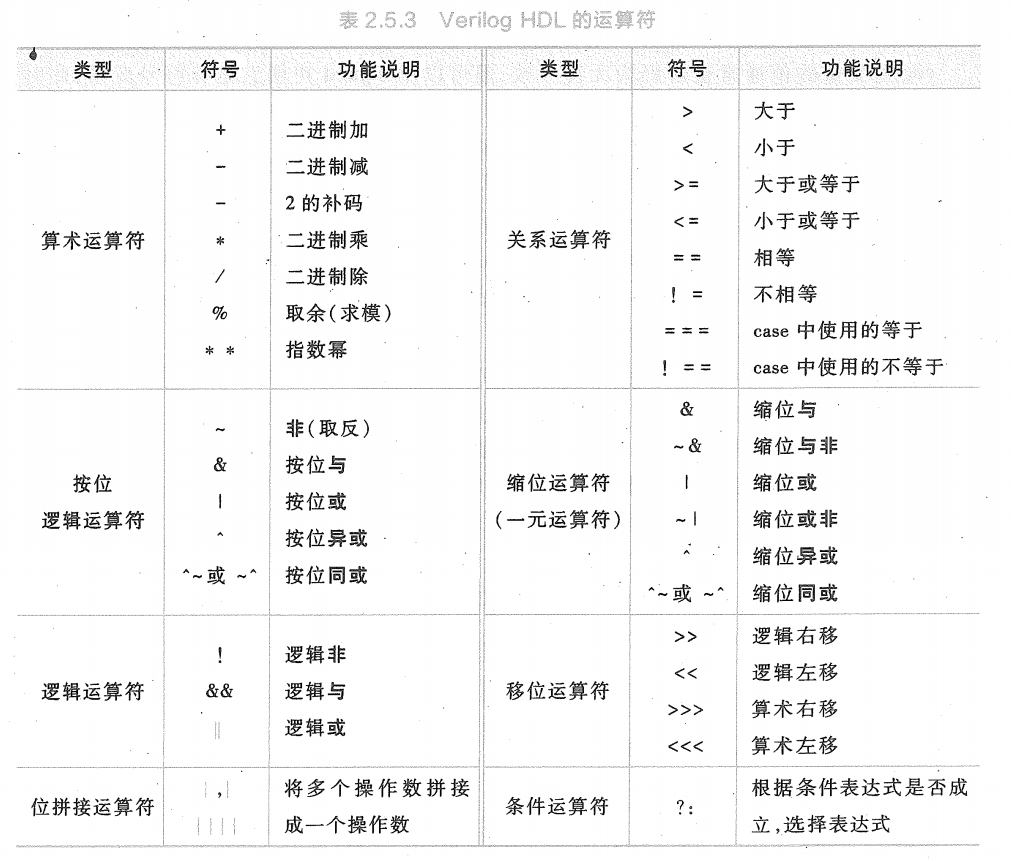
算术运算符的操作数是数值。运算符+、-、* 、/用来对一对操作数求和、差、积、商。取余运算符(%)求两个数相除的余数。指数幂运算符(**)是Verilog-2001中新增加的，底数和指数可以是实数型、整数型或带符号数，结果为双精度浮点数值。

按位(bitwise)运算是将两个操作数的对应位进行相应的逻辑运算，操作数是几位数，则运算结果也是几位数。

取反运算符(~)是一元运算符，它对一个向量操作数进行取反，结果还是向量。

缩位(reduction)运算符是一元运算符，它和按位运算符是不同的。缩位运算是对单个操作数的各位进行相应运算(从右到左一位一位地进行运算)，产生的结果是1位二进制数。注意，负数不能使用缩位运算符。

逻辑运算的结果为1位，它用来判断条件的真假，如果条件为真，结果为1；如果条件是假，结果为0；如果条件是不确定的，结果将是x。

逻辑运算符!为一元运算符，而 &&和||为二元运算符。如果操作数只有1位，那么1代表逻辑1，0代表逻辑0；如果操作数由多位组成，若操作数的每一位都是0，则认为该操作数具有逻辑0值；反之,若操作数中某一位为1，则认为该操作数具有逻辑1值；如果任一个操作数为x或z，则逻辑运算的结果为不定态x。

A=4'b1010

B=4'b1111

表2.5.4为上述三种不同运算的比较。

位拼接运算符的作用是将两个或多个信号的某些位拼接起来成为一个新的操作数，进行运算操作。例如，设A=1'b1，B=2'b10，C = 2'b00，若将操作数B、C拼接起来，则得到{B,C}= 4'b1000；若将操作数A、操作数B的第1位和C的第0位拼接起来，则得到一个3位向量的新操作数，即{A,B[ 1],c[0]} =3'b110。若将操作数A、B、C和 3'b101拼接起来，则得到一个8位向量的新操作数，即{A, B,C,3'b101}= 8'b11000101。

对同一个操作数重复拼接还可以使用双重大括号构成的运算符{{}}，例如{4{A} }=4'b1111,{2{A},2{B},C} =8'b11101000。

注意，参与拼接的操作数必须标明位宽。

关系运算的结果为1位，可用来判断条件的真假，如果条件为真，结果为1；如果条件是假，结果为0；如果条件是不确定的，结果将是x。

在Verilog 四值逻辑(0、1、x、z)系统中，关系运算符===和!==按位测试两个数值相同还是不同。

例如，如果'A = 4'b1xx0、B =4'b1xx0，那么A===B的结果为真，但是A==B的结果为x。

Verilog-2001有逻辑移位运算符和算术移位运算符。逻辑移位时，空出的位用0填充，例如，逻辑右移时，左边空出的位用0填充。算术右移时，空出的位要用左边最高位(MSB)的数值来填充。例如，A= 11010，则执行A>>>1后，结果为A=11101。逻辑左移与算术左移没有区别。

（2）运算符的优先级

Verilog主要运算符的优先级如表2.5.5所示。优先级的顺序从下向上依次增加。列在同一行的运算符优先级别相同。所有运算符(条件运算符?:除外)在表达式中都是从左向右结合的，使用圆括号()可以改变运算的先后顺序。为了避免发生误解，推荐使用圆括号去隔开不同的表达式，以使代码的含义更明确易懂。

2.5.6 Verilog HDL 内部的基本门级元件

Verilog语言包含12个预先定义的基本门级元件( gate level primitives)模型，如表2.5.6所示。在门级建模时，可以直接调用这些基本门级元件将逻辑图转换成Verilog 代码。

注意，门级元件均用小写的关键词来表示，当使用这些元件进行逻辑仿真时，仿真软件会根据程序的描述给每个元件中的信号分配逻辑0、逻辑1、不确定态x和高阻态z这4个值之一。下面介绍这些元件的用法。

（1）多输入门

and、nand、or、nor、xor和xnor是具有多个输入的逻辑门，它们的共同特点是：只允许有一个输出，但可以有多个输入。

与门元件( and)模型的示意图如图2.5.10所示，逻辑真值表如表2.5.7所示，两个输入分别列于表中行的顶部和列的左侧，行、列输入的运算结果列在表的中间部位。注意，只有当行、列输入都是1时，行列交叉处的输出才为1；而任意一个输入为0，输出就为为0；另外，如果有一个输入为x或者z，则输出为x或者z。多输入门的输出不可能为高阻态z。

与门元件的一般调用形式为：

and A1(out , in1 , in2 ,……, inN ) ;

其中，实例名A1可以省略。在后面的圆括号中列出该门的端口，输出列在前，输入列在后；并用逗号分开。

nand , or , nor , xor, xnor的调用形式与之类似，不再赘述。表2.5.8和表2.5.9是两输入端or和异或xor元件的逻辑真值表。

（2）多输出门

buf、not是具有多个输出端的逻辑门，它们的共同特点是：允许有多个输出，但只有一个输入。

一般的调用形式为：

buf B1( out1 , out2 , … , outN , in );
not N1( outl , out2 , … , outN , in );

其中，实例名B1、N1可以省略。图2.5.11所示为多个输出端反相器的示意图，其逻辑真值表如表2.5.10所示。buf逻辑真值表与not 的类似，但其输出的0、1值与not的相反。

（3）三态门

bufif1、bufif0、notif1和notif0是三态门元件模型。

这些门有一个输出、一个数据输入和一个控制输入。

如果输入控制信号无效，则三态门的输出为高阻态z。

（注：该关键词可分两部分理解，buf是 buffer的缩写，表示该元件完成缓冲器的功能；后面的if1是如果为1，表示完成该功能所需的条件。其他3个关键词的理解与此类似）