线段树算法详解与实现

原创于 2025-10-12 17:54:37 发布 · 951 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #图论

线段树常见场景

节点最大个数为区间长度4倍

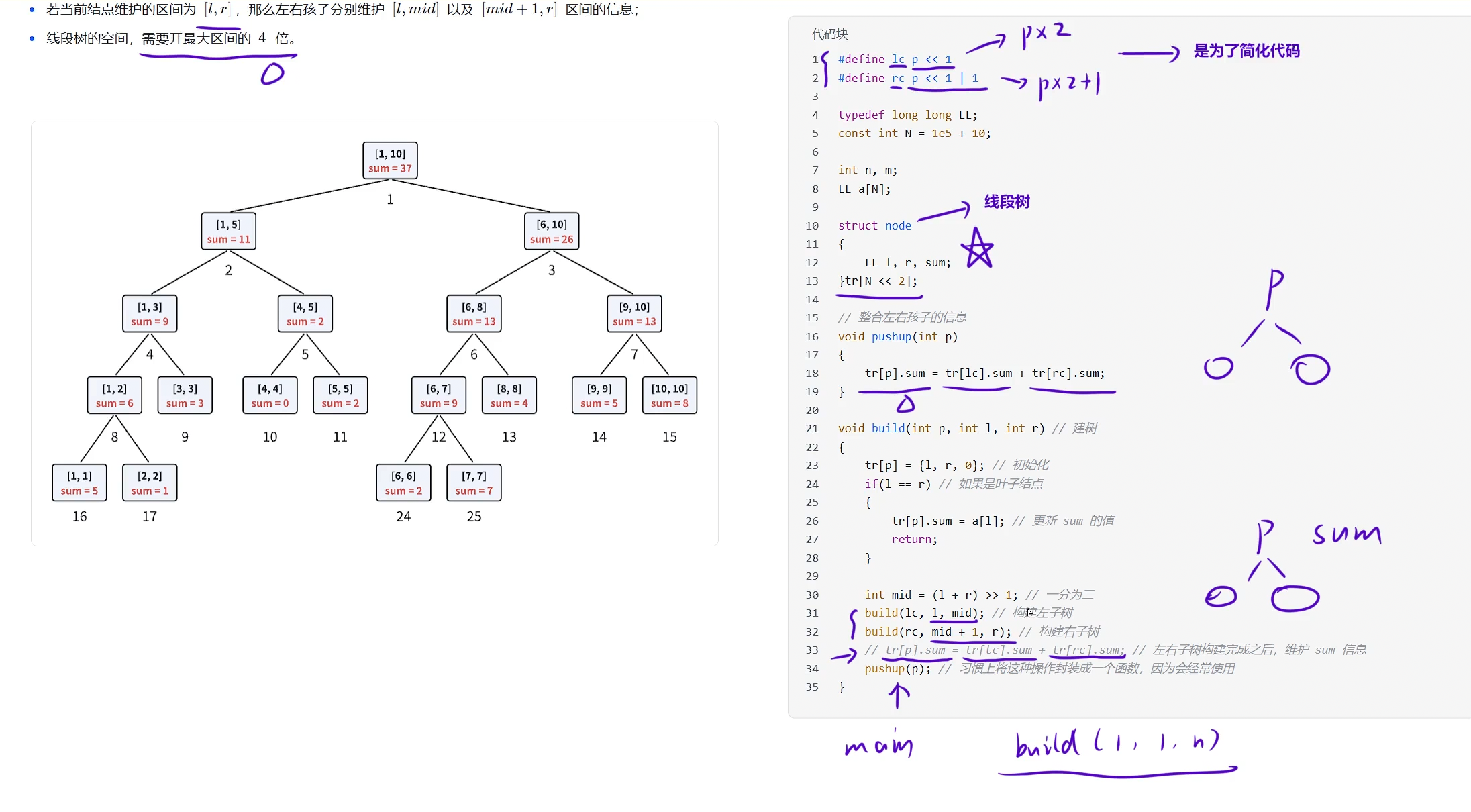
单点修改模版P3374 【模板】树状数组 1 - 洛谷

#include<iostream>
using namespace std;
#define lc p<<1
#define rc p<<1|1
const int N = 5e5 + 10;
int n, m;
int a[N];
struct node 
{
	int l, r, sum; 
}tr[4*N];
void pushup(int p)
{
	tr[p].sum = tr[lc].sum + tr[rc].sum;
}
void build(int p, int l, int r)
{
	tr[p] = { l,r,0 };
	if (l == r)
	{
		tr[p].sum = a[l]; return;
	}
	
	int mid = (l + r) / 2;
	build(lc, l, mid);
	build(rc, mid + 1, r);
	
	pushup(p);
}
int query(int p,int x,int y)
{
	int l = tr[p].l, r = tr[p].r;

	if (x <= l && y >= r)return tr[p].sum;

	int ret = 0; int mid = (l + r) / 2;
	if (x <= mid)ret += query(lc, x, y);
	if (y >= mid + 1)ret += query(rc, x, y);

	return ret;
}
void modify(int p, int x, int k)
{
	int l = tr[p].l, r = tr[p].r;
	if (l == r)
	{
		tr[p].sum += k; return;
	}

	int mid = (l + r) / 2;
	if (x <= mid)modify(lc, x, k);
	else modify(rc, x, k);

	pushup(p);
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)cin >> a[i];
	build(1, 1, n);

	for (int i = 1; i <= m; i++)
	{
		int a; cin >> a;
		if (a == 1)
		{
			int x, k; cin >> x >> k;
			modify(1, x, k);
		}
		else
		{
			int x, y; cin >> x >> y;
			cout<<query(1, x, y)<<endl;
		}
	}
	return 0;
}

区间修改及查询操作案例：P3372 【模板】线段树 1 - 洛谷

经常不注意会踩的坑：(以区间+操作为例)

1.sum,add操作时均为+=

2.modify在修改左右子树前也要pushdown下放懒标记(modify中的最后操作会pushup)

3.query操作中记得pushdown

4.pushdown操作中记得判断add

const int N = 1e5 + 10;
#define lc p<<1
#define rc p<<1|1
typedef long long LL;
LL a[N]; int n, m;
struct node
{
	int l, r;
	LL sum, add;
}tr[4*N];
void pushup(int p)
{
	tr[p].sum = tr[lc].sum + tr[rc].sum;
}


void build(int p, int l, int r)
{
	tr[p] = { l,r,0,0 };
	if (l == r)
	{
		tr[p].sum = a[l];
		return;
	}

	int mid = (l + r)/2;
	build(lc, l, mid); build(rc, mid + 1, r);
	pushup(p);

}
void lazy(int p, LL add)
{
	//已在pushdown检查是否有懒标记了，此处记得均为+=
	int l = tr[p].l, r = tr[p].r;
	tr[p].sum += (r - l + 1) *add;
	tr[p].add += add;
}
void pushdown(int p)
{
	if(tr[p].add)//先看是否有懒标记
	{
		lazy(lc, tr[p].add);
		lazy(rc, tr[p].add);
		tr[p].add = 0;
	}
}
void modify(int p, int x, int y, int k)
{
	int l = tr[p].l, r = tr[p].r;
	if (x <= l && y >= r)
	{
		/*tr[p].sum += (r - l + 1) * k;
		tr[p].add += k;*/
		lazy(p, k);
		return;
	}
	pushdown(p);//因为modify最后的操作是pushup，多次modify时为防止原值pushup导致算错，要pushdown更新

	int mid = (l + r) / 2;
	if (x <= mid)modify(lc, x, y, k);
	if (y> mid)modify(rc, x, y, k);

	pushup(p);

}
LL query(int p, int x, int y)
{
	int l = tr[p].l, r = tr[p].r;
	if (x <= l && y >= r)return tr[p].sum;

	pushdown(p); //懒标记下放

	int mid = (l + r) / 2; LL ret = 0;
	if (x <= mid)ret+=query(lc, x, y);
	if (y > mid)ret += query(rc, x, y);

	return ret;
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)cin >> a[i];
	build(1, 1, n);
	for (int i = 1; i <= m; i++)
	{
		int a; cin >> a;
		if (a == 1)
		{
			int x, y, k; cin >> x >> y >> k;
			modify(1, x, y, k);
		}
		else
		{
			int x, y; cin >> x >> y;
			cout << query(1, x, y) << endl;
		}
	}
	return 0;
}

重难点：线段树多个区间修改操作

1.P3373 【模板】线段树 2 - 洛谷

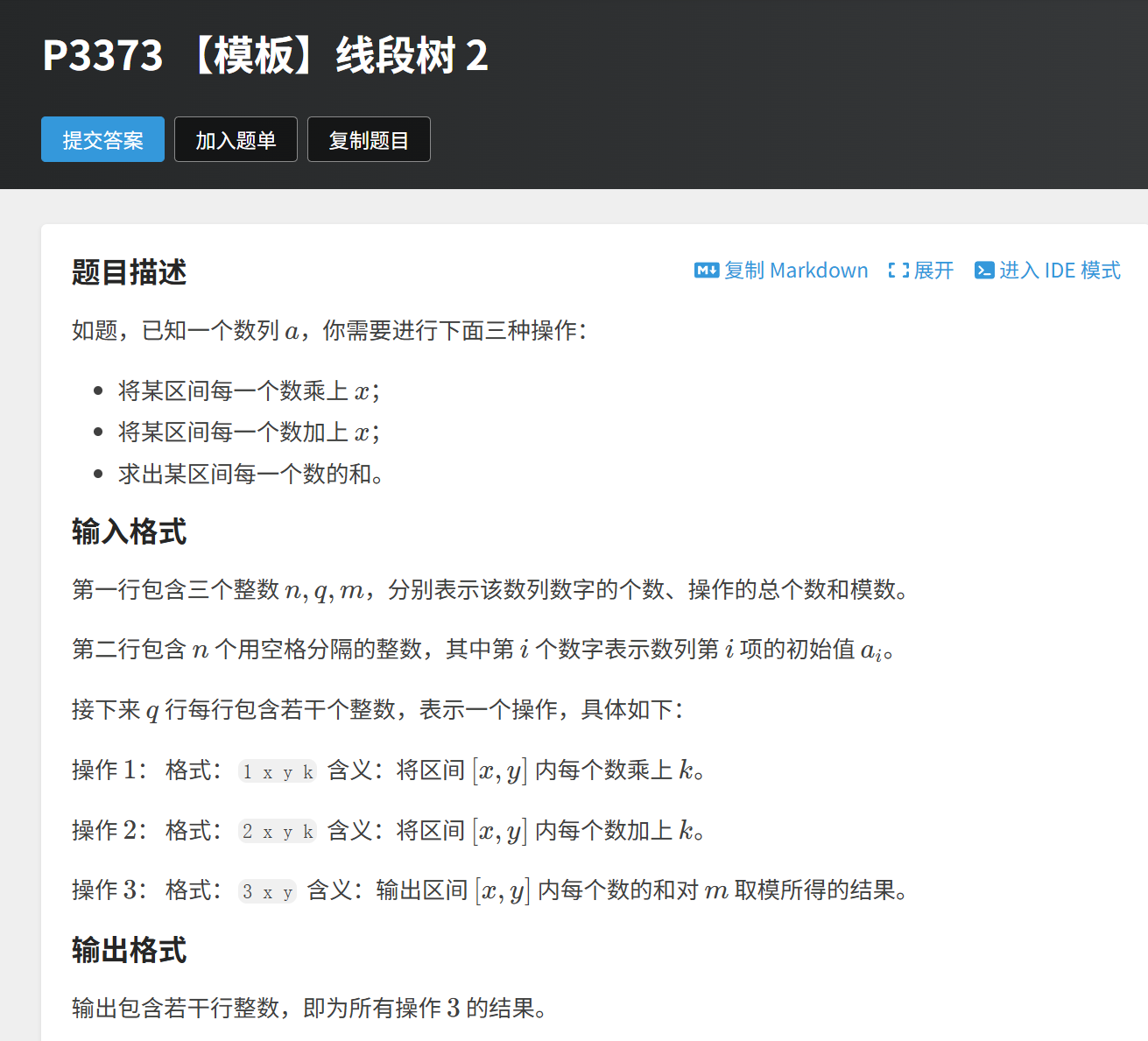
既有+又有*，无法判断谁先操作，那就假设规定（推导数学公式来保证正确性）

在懒标记下放时我们规定：每一步都是

先加后乘，推导数学式如下图，我们发现更新add时（a'=a+A/m）可能会导致精度丢失

而先乘后加我们发现不存在此问题，故而使用它

s1表示的是该区间原来之和，最后将其拆出是为了延续公式的一般性

s2表示的是该区间现在之和

s3表示的是懒标记传递至此处时该区间更新后之和

#include<iostream>
using namespace std;
typedef long long LL;
//此题数据范围极大，LL也会越界，必须在不断更新区间时就对其进行摸操作，
//只在query是取模仍会出现负数
#define lc p<<1
#define rc p<<1|1
const int N = 1e5 + 10;
struct node
{
	int l, r;
	LL sum, add, mul;
}tr[N<<2];
int n, q, mod;
int a[N];
void pushup(int p)
{
	tr[p].sum = tr[lc].sum + tr[rc].sum;
}
void build(int p, int l, int r)
{
	tr[p] = { l,r,a[l],0,1 };
	if (l == r)return;

	int mid = (l + r) / 2;
	build(lc, l, mid); build(rc, mid + 1, r);

	pushup(p);
}
void lazy(int p, LL add, LL mul)
{
	tr[p].sum = (tr[p].sum * mul + (tr[p].r - tr[p].l + 1) * add)%mod;
	tr[p].add = (tr[p].add * mul + add)%mod;
	tr[p].mul = (tr[p].mul * mul)%mod;
}
// void lazy(int p, LL add, LL mul)
// {
// 	int len = tr[p].r - tr[p].l + 1;
// 	tr[p].sum = tr[p].sum * mul + add * len;
// 	tr[p].mul *= mul;
// 	tr[p].add = tr[p].add * mul + add;
// }
void pushdown(int p)
{
	if (tr[p].add != 0 || tr[p].mul != 1)
	{
		lazy(lc, tr[p].add, tr[p].mul);
		lazy(rc, tr[p].add, tr[p].mul);
		tr[p].add = 0;
		tr[p].mul = 1;
	}
}
void modify(int p, int x, int y, LL add, LL mul)
{
	int l = tr[p].l, r = tr[p].r;
	if (x <= l && y >= r)
	{
		lazy(p, add, mul);
		return;
	}

	pushdown(p);

	int mid = (l + r) / 2;
	if (x <= mid)modify(lc, x, y, add, mul);
	if (y > mid)modify(rc, x, y, add, mul);
	pushup(p);
}
LL query(int p, int x, int y)
{
	int l = tr[p].l, r = tr[p].r;
	if (x <= l && y >= r)return tr[p].sum;

	pushdown(p);
	int mid = (l + r) / 2; LL ret = 0;
	if (x <= mid)ret += query(lc, x, y);
	if (y > mid)ret += query(rc, x, y);
	return ret%mod;
}
int main()
{
	cin >> n >> q >> mod;

	for (int i = 1; i <= n; i++)cin >> a[i];
	build(1, 1, n);

	while (q--)
	{
		int op, x, y, k;
		cin >> op;
		if (op == 1)
		{
			cin >> x >> y >> k;
			modify(1, x, y, 0, k);
		}
		else if (op == 2)
		{
			cin >> x >> y >> k;
			modify(1, x, y, k, 1);

		}
		else
		{
			cin >> x >> y;
			cout << query(1, x, y) << endl;;
		}
	}

}

2.P1253 扶苏的问题 - 洛谷

#include<iostream>
using namespace std;
typedef long long LL;
#define lc p<<1
#define rc p<<1|1
const int N = 1e6 + 10;
int a[N];
int n, m;
struct node
{
	int l, r;
	LL max, add, update;
	bool st;
}tr[N<<2];
void pushup(int p)
{
	tr[p].max = max(tr[lc].max, tr[rc].max);
}
void build(int p,int l,int r)
{
	tr[p] = { l,r,a[l],0,0,false };
	if (l == r)return;

	int mid = (l + r) / 2;
	build(lc, l, mid); build(rc, mid + 1, r);
	pushup(p);
}
void lazy(int p, LL add, LL update, bool st)
{
	if (st)
	{
		tr[p].max = update;
		tr[p].add = 0;
		tr[p].update = update;
		tr[p].st = true;
	}
	tr[p].max += add;
	tr[p].add += add;
	
}
void pushdown(int p)
{
	lazy(lc, tr[p].add, tr[p].update, tr[p].st);
	lazy(rc, tr[p].add, tr[p].update, tr[p].st);
	tr[p].add = tr[p].update = tr[p].st = 0;
}
void modify(int p, int x, int y, LL add, LL update,bool st)
{
	int l = tr[p].l, r = tr[p].r;
	if (x <= l && y >= r)
	{
		lazy(p, add, update,st);
		return;
	}

	pushdown(p);
	int mid = (l + r) / 2;
	if (x <= mid)modify(lc, x, y, add, update,st);
	if (y > mid)modify(rc, x, y, add, update,st);

	pushup(p);
}
LL query(int p, int x, int y)
{
	int l = tr[p].l, r = tr[p].r;
	if (x <= l && y >= r)return tr[p].max;

	pushdown(p);

	int mid = (l + r) / 2;LL ret = -1e18;
	if (x <= mid)ret = max(ret, query(lc, x, y));
	if (y > mid)ret = max(ret, query(rc, x, y));

	return ret;
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)scanf("%d", &a[i]);
	build(1, 1, n);

	for (int i = 1; i <= m; i++)
	{
		int op; scanf("%d",&op);
		if (op == 1)
		{
			int x, y, k; scanf("%d%d%d", &x, &y, &k);
			modify(1, x, y, 0, k, true);
		}
		else if (op == 2)
		{
			int x, y, k; scanf("%d%d%d", &x, &y, &k);

			modify(1, x, y, k, 0, false);
		}
		else
		{
			int x, y; scanf("%d%d", &x, &y);
			printf("%ld\n",query(1,x,y));
		}
	}
	return 0;
}

练习部分

P3368 【模板】树状数组 2 - 洛谷

typedef long long LL;
#define lc p<<1
#define rc p<<1|1
const int N = 5e5 + 10;
int a[N];
int n, m;
struct node
{
	int l, r;
	LL sum, add;
}tr[N << 2];
void pushup(int p)
{
	tr[p].sum = tr[lc].sum + tr[rc].sum;
}
void build(int p, int l, int r)
{
	tr[p] = { l,r,a[l],0 };
	if (l == r)return;

	int mid = (l + r) / 2;
	build(lc, l, mid); build(rc, mid + 1, r);
	pushup(p);
}
void lazy(int p, int k)
{
	tr[p].sum += (tr[p].r - tr[p].l + 1) * k;
	tr[p].add += k;
}
void pushdown(int p)
{
	if (tr[p].add)
	{
		lazy(lc, tr[p].add);
		lazy(rc, tr[p].add);
		tr[p].add = 0;
	}
}
void modify(int p, int x, int y, int k)
{
	int l = tr[p].l, r = tr[p].r;
	if (x <= l && y >= r)
	{
		lazy(p, k);
		return;
	}
	pushdown(p);

	int mid = (l + r) / 2;
	if (x <= mid)modify(lc, x, y, k);
	if (y > mid)modify(rc, x, y, k);
	pushup(p);
}
int query(int p, int x)
{
	int l = tr[p].l, r = tr[p].r;
	if (l == r)return tr[p].sum;

	pushdown(p);

	int mid = (l + r) / 2; int ret = 0;
	if (x <= mid)ret += query(lc, x);
	else ret += query(rc, x);
	return ret;
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)scanf("%d", &a[i]);
	build(1, 1, n);

	for (int i = 1; i <= m; i++)
	{
		int a; cin >> a;
		if (a == 1)
		{
			int x, y, k; cin >> x >> y >> k;
			modify(1, x, y, k);
		}
		else
		{
			int x; cin >> x;
			printf("%d\n", query(1, x));
		}
	}
}

P3870 [TJOI2009] 开关 - 洛谷

#include<iostream>
using namespace std;
#define lc p<<1
#define rc p<<1|1
const int N = 2e5 + 10;
struct node
{
	int l, r, ret, cnt;
}tr[N<<2];
int n, m;
void pushup(int p)
{
	tr[p].ret = tr[lc].ret + tr[rc].ret;
}
void build(int p, int l, int r)
{
	tr[p] = { l,r,0,0 };
	if (l == r)return;

	int mid = (l + r) / 2;
	build(lc, l, mid);
	build(rc, mid + 1, r);
}
void lazy(int p)
{
	tr[p].ret = (tr[p].r - tr[p].l + 1) - tr[p].ret;
	tr[p].cnt += 1;
}
void pushdown(int p)
{
	if (tr[p].cnt % 2)
	{
		lazy(lc);
		lazy(rc);
	}
	tr[p].cnt = 0;
}
void modify(int p,int x,int y)
{
	int l = tr[p].l, r = tr[p].r;

	if (x <= l && y >= r)
	{
		lazy(p);
		return;
	}

	pushdown(p);

	int mid = (l + r) / 2;
	if (x <= mid)modify(lc, x, y);
	if (y > mid)modify(rc, x, y);

	pushup(p);
}
int query(int p, int x, int y)
{
	int l = tr[p].l, r = tr[p].r;

	if (x <= l && y >= r)return tr[p].ret;

	pushdown(p);

	int mid = (l + r) / 2; int ret = 0;
	if (x <= mid)ret += query(lc, x, y);
	if (y > mid)ret += query(rc, x, y);

	return ret;
}
int main()
{
	cin >> n >> m;
	build(1, 1, n);
	for (int i = 1; i <= m; i++)
	{
		int a,x,y; cin >> a>>x>>y;
		if (!a)
		{
			modify(1, x, y);
		}
		else
		{
			cout << query(1, x, y) << endl;
		}
	}
	return 0;
}

P1438 无聊的数列 - 洛谷

本题是区间等差修改+单点查询操作，故而可用线段树+差分数组。可减少代码细节错误率

#include<iostream>
using namespace std;
typedef long long LL;
#define lc p<<1
#define rc p<<1|1
const int N = 1e5 + 10;
int a[N], n, m;
struct node
{
	LL l, r, sum, A, D;
}tr[N<<2];
void pushup(int p)
{
	tr[p].sum = tr[lc].sum + tr[rc].sum;
}
void build(int p, int l, int r)
{
	tr[p] = { l,r,a[l],0,0 };
	if (l == r)return;

	int mid = (l + r) / 2;
	build(lc, l, mid); build(rc, mid + 1, r);

	pushup(p);
}
void lazy(int p, LL a, LL d)
{
	int len = tr[p].r - tr[p].l + 1;
	tr[p].sum += len * a + len * (len - 1) * d / 2;
	tr[p].A += a;
	tr[p].D += d;
}
void pushdown(int p)
{
	if (tr[p].A||tr[p].D)
	{
		int l = tr[p].l, r = tr[p].r;
		int mid = (r+l) / 2;
		lazy(lc, tr[p].A, tr[p].D);
		lazy(rc, tr[p].A+(mid+1-l)*tr[p].D, tr[p].D);//虽然能pushdown说明此范围全是可修改区域，但不能用mid*d,而是(mid+1-l)*d,要的是区间长度
		tr[p].A = 0;
		tr[p].D = 0;
	}
}
void modify(int p, int x, int y, LL a, LL k)
{
	int l = tr[p].l, r = tr[p].r;
	if (x <= l && y >= r)
	{
		lazy(p, a+(l-x)*k, k);
		return;
	}

	pushdown(p);
	int mid = (l + r) / 2;
	if (x <= mid)modify(lc, x, y, a, k);
	if (y > mid)modify(rc, x, y, a, k);
	pushup(p);
}
LL query(int p, int x)
{
	int l = tr[p].l, r = tr[p].r;
	if (l == r)return tr[p].sum;
	
	pushdown(p);

	int mid = (l + r) / 2; LL ret = 0;
	if (x <= mid)ret+=query(lc, x);
	else ret+=query(rc, x);

	return ret;
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)cin >> a[i];
	build(1, 1, n);

	for (int i = 1; i <= m; i++)
	{
		int a; cin >> a;
		if (a == 1)
		{
			int x, y, a, k; cin >> x >> y >> a >> k;
			modify(1, x, y, a, k);
		}
		else
		{
			int x; cin >> x;
			cout << query(1, x) << endl;
		}
	}
}

重难点：线段树+分治

1.P4513 小白逛公园 - 洛谷

#include<iostream>
using namespace std;
#define lc p<<1
#define rc p<<1|1

const int N = 5e5 + 10;
int n, m, a[N];
struct node
{
	int l, r, max, lmax, rmax, sum;
}tr[N<<2];
void pushup(node& p,node& l,node&r)
{
	p.max = max(max(r.max, l.max), l.rmax+r.lmax);
	p.lmax = max(l.lmax, l.sum + r.lmax);
	p.rmax = max(r.rmax, r.sum + l.rmax);
	p.sum = l.sum + r.sum;
}
void build(int p, int l, int r)
{
	tr[p] = { l,r,a[l],a[l],a[l],a[l]};
	if (l == r)return;

	int mid = (l + r) / 2;
	build(lc, l, mid); build(rc, mid + 1, r);
	pushup(tr[p],tr[lc],tr[rc]);
}
void modify(int p, int x, int k)
{
	int l = tr[p].l, r = tr[p].r;
	if (l == r)
	{
		tr[p].max = tr[p].lmax = tr[p].rmax = tr[p].sum = k;
		return;
	}

	int mid = (l + r) / 2;
	if (x <= mid)modify(lc, x, k);
	else modify(rc, x, k);

	pushup(tr[p], tr[lc], tr[rc]);

}
node query(int p, int x, int y)
{
	int l = tr[p].l, r = tr[p].r;
	if (x <= l && y >= r)return tr[p];

	int mid = (l + r) / 2;

	
	
	if (y <= mid)return query(lc, x, y);
	if (x > mid)return query(rc, x, y);
	
	node ret, L = query(lc, x, y), R = query(rc, x, y);
	pushup(ret, L, R);
	return ret;
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)cin >> a[i];
	build(1, 1, n);

	for (int i = 1; i <= m; i++)
	{
		int op; cin >> op;
		if (op == 1)
		{
			int x, y; cin >> x >> y;
			if (x > y)swap(x, y);
			cout<<query(1, x, y).max<<endl;
		}
		else
		{
			int x, k; cin >> x >> k;
			modify(1, x, k);
		}
	}
}

线段树+剪枝

P4145 上帝造题的七分钟 2 / 花神游历各国 - 洛谷

区间修改+区间查询但我们发现区间无法直接修改，即无法正常使用懒标记（正常使用懒标记是指：当前节点可以直接修改，并不依赖子节点）。

此题意味着修改时我们需要每次都遍历子节点，时间复杂度为m*n*logn，还不如直接使用数组（复杂度为n*m），那我们看看能否使用剪枝操作来降低时间复杂度。

思路：

我们又发现10^12最多开根6次变成了1，到了1时就没必要开根了（1开根仍为1）

那我们在node节点中存储一个max(区间最大值)不就能监视到区间当前还有无必要开根了吗

即当前区间中的最大值为1时就可以返回了

总结：

遍历一次线段树时间复杂度为n*logn,而最多开根6次就无需开根，即最多遍历6次完整的线段树就可以使得其区间最大值为1，故而使用剪枝后的时间复杂度为6*n*logn(与修改次数m无关了，6次之后进来即返回)

#include<iostream>
#include<cmath>
using namespace std;
typedef long long LL;
#define lc p<<1
#define rc p<<1|1
const int N = 1e5 + 10;
int n, m;
LL a[N];
struct node
{
	int l, r;
	LL max, sum;
}tr[N<<2];
void pushup(int p)
{
	tr[p].sum = tr[lc].sum + tr[rc].sum;
	tr[p].max = max(tr[lc].max, tr[rc].max);
}
void build(int p, int l, int r)
{
	tr[p] = { l,r,a[l],a[l] };
	if (l == r)return;

	int mid = (l + r) / 2;
	build(lc, l, mid); build(rc, mid + 1, r);
	pushup(p);

}

void modify(int p, int x, int y)
{
	if (tr[p].max == 1)return;

	int l = tr[p].l, r = tr[p].r;
	if (l == r)
	{
		tr[p].sum = sqrt(tr[p].sum);
		tr[p].max = sqrt(tr[p].max);
		return;
	}

	int mid = (l + r) / 2;
	if (x <= mid)modify(lc, x, y);
	if (y > mid)modify(rc, x, y);

	pushup(p);
}
LL query(int p, int x, int y)
{
	int l = tr[p].l, r = tr[p].r;
	if (x <= l && y >= r)return tr[p].sum;

	int mid = (l + r) / 2; LL ret = 0;
	if (x <= mid)ret += query(lc,x,y);
	if (y > mid)ret += query(rc, x, y);

	return ret;

}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> a[i];
	build(1, 1, n);
	cin >> m;
	for (int i = 1; i <= m; i++)
	{
		int op, x, y; cin >> op >> x >> y;
        if (x > y)swap(x, y);
		if (op == 0)
		{
			modify(1, x, y);
		}
		else
		{
			cout<<query(1, x, y)<<endl;
		}
	}
	
}

权值线段树+离散化

P1908 逆序对 - 洛谷

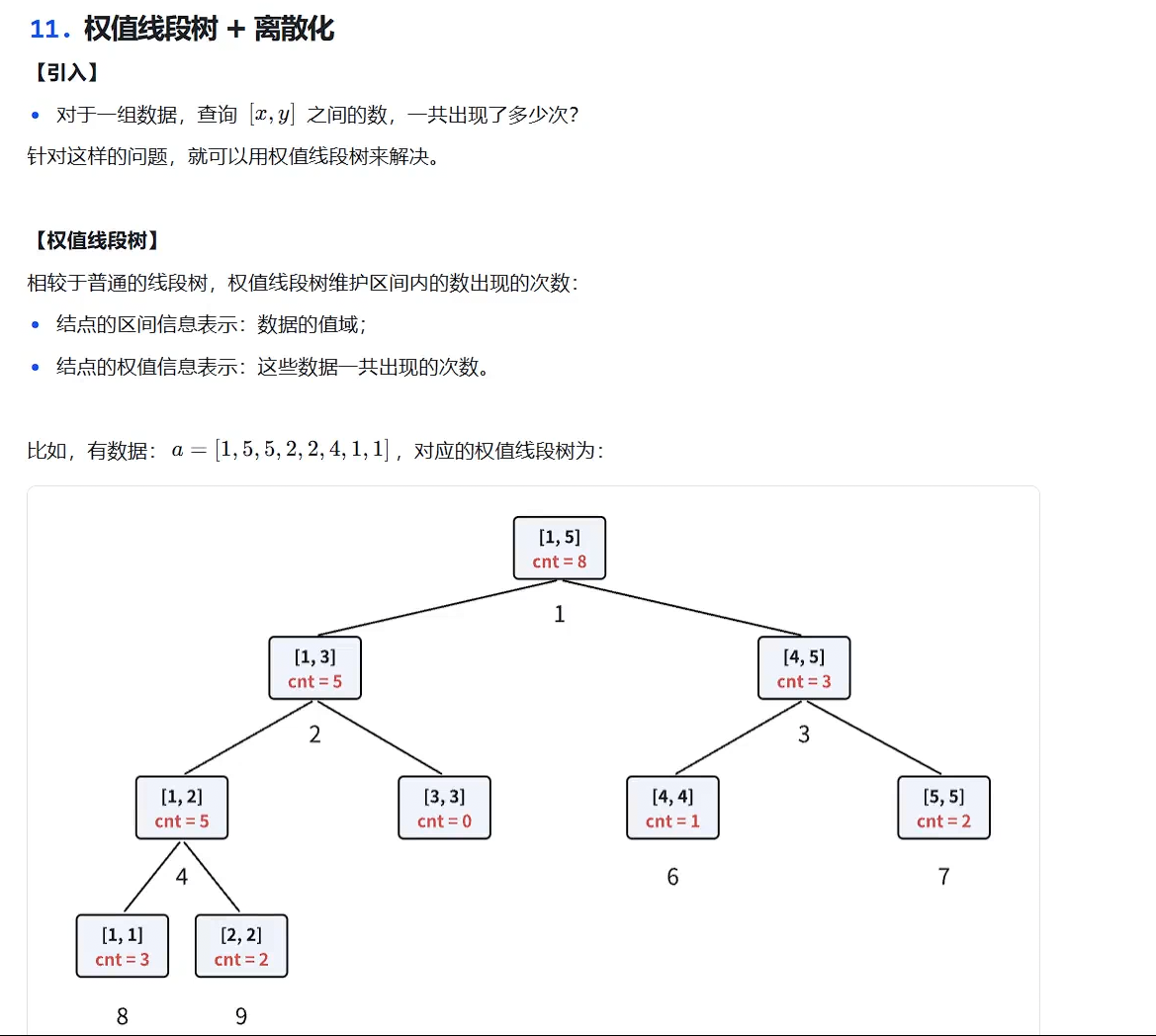
上面注释掉的两种方法是分治思想实现的：全队是基于归并排序

而今天讲的线段树方法是一遍查询区间，一边更新线段树

#include<iostream>//时间复杂度为n*logn^2(sort的缘故)
#include<algorithm>
using namespace std;
// const int N = 5e5 + 10;
// int a[N];
// int tmp[N];
// long long ret;
//void dfs(int left, int right)
//{
//    if (left == right)return;
//    if (right - left == 1)
//    {
//        if (a[left] > a[right])ret += 1;
//        return;
//    }
//    int mid = (left + right) / 2;
//    dfs(left, mid);
//    dfs(mid + 1, right);
//
//    sort(a + left, a + mid + 1);
//    sort(a + mid + 1, a + right + 1);
//    int start1 = left, end1 = mid;
//    int start2 = mid + 1, end2 = right;
//    while (start1 <= end1 && start2 <= end2)
//    {
//        if (a[start1] > a[start2])
//        {
//            ret += end1 - start1 + 1;
//            start2++;
//        }
//        else
//        {
//            start1++;
//        }
//    }
//}
//int main()
//{
//    int n; cin >> n;
//    for (int i = 1; i <= n; i++)cin >> a[i];
//
//    dfs(1, n);
//    cout << ret << endl;
//}

// void merge(int left, int right)
// {
//     if (left >= right)return;

//     int mid = (left + right) / 2;
//     merge(left, mid);
//     merge(mid + 1, right);

//     int start1 = left, end1 = mid;
//     int start2 = mid + 1, end2 = right;
//     int i = left;
//     while (start1 <= end1 && start2 <= end2)
//     {
//         if (a[start1] > a[start2])
//         {
//             ret += end1 - start1 + 1;
//             tmp[i++] = a[start2];
//             start2++;
//         }
//         else
//         {
//             tmp[i++] = a[start1];
//             start1++;
//         }
//     }
//     while (start1 <= end1)tmp[i++] = a[start1++];
//     while (start2 <= end2)tmp[i++] = a[start2++];
//     for (int j = left; j <= right; j++)a[j] = tmp[j];

// }
// int main()
// {
//     int n; cin >> n;
//     for (int i = 1; i <= n; i++)cin >> a[i];

//     merge(1, n);
//     cout << ret << endl;
// }

typedef long long LL;
#include<unordered_map>
#define lc p<<1
#define rc p<<1|1
const int N = 5e5 + 10;
int a[N], t[N];
int n, pos;//pos来表示离散化后的最大的数
unordered_map<int, int>mp; 
struct node
{
	int l, r;
	LL cnt;
}tr[N<<2];
void pushup(int p)
{
	tr[p].cnt = tr[lc].cnt + tr[rc].cnt;
}
void build(int p,int l,int r)
{
	tr[p] = { l,r,0 };
	if (l == r)return;

	int mid = (l + r) >> 1;
	build(lc, l, mid); build(rc, mid + 1, r);
	//pushup(p);   此题此处不用
}
LL query(int p, int x, int y)
{
	int l = tr[p].l, r = tr[p].r;
	if (x <= l && y >= r)return tr[p].cnt;

	int mid = (l + r) / 2; LL ret = 0;
	if (x <= mid)ret += query(lc, x, y);
	if (y > mid)ret += query(rc, x, y);
	return ret;
}
void modify(int p, int x)
{
	int l = tr[p].l, r = tr[p].r;
	if (l==r)
	{
		tr[p].cnt++; 
		return;
	}
	int mid = (l + r) / 2;
	if (x <= mid)modify(lc, x);
	else modify(rc, x);

	pushup(p);
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i]; t[i] = a[i];
	}
	//离散化
	sort(t + 1, t + n + 1);
	for (int i = 1; i <= n; i++)
	{
		if (mp.count(t[i]))continue;
		mp[t[i]] = ++pos;
	}

	build(1, 1, pos);
	LL ret = 0;
	for (int i = 1; i <= n; i++)
	{
		int x = mp[a[i]];
		ret+=query(1, x + 1, pos);
		modify(1, x);
	}
	cout << ret << endl;
}

线段树+数学

P5142 区间方差 - 洛谷

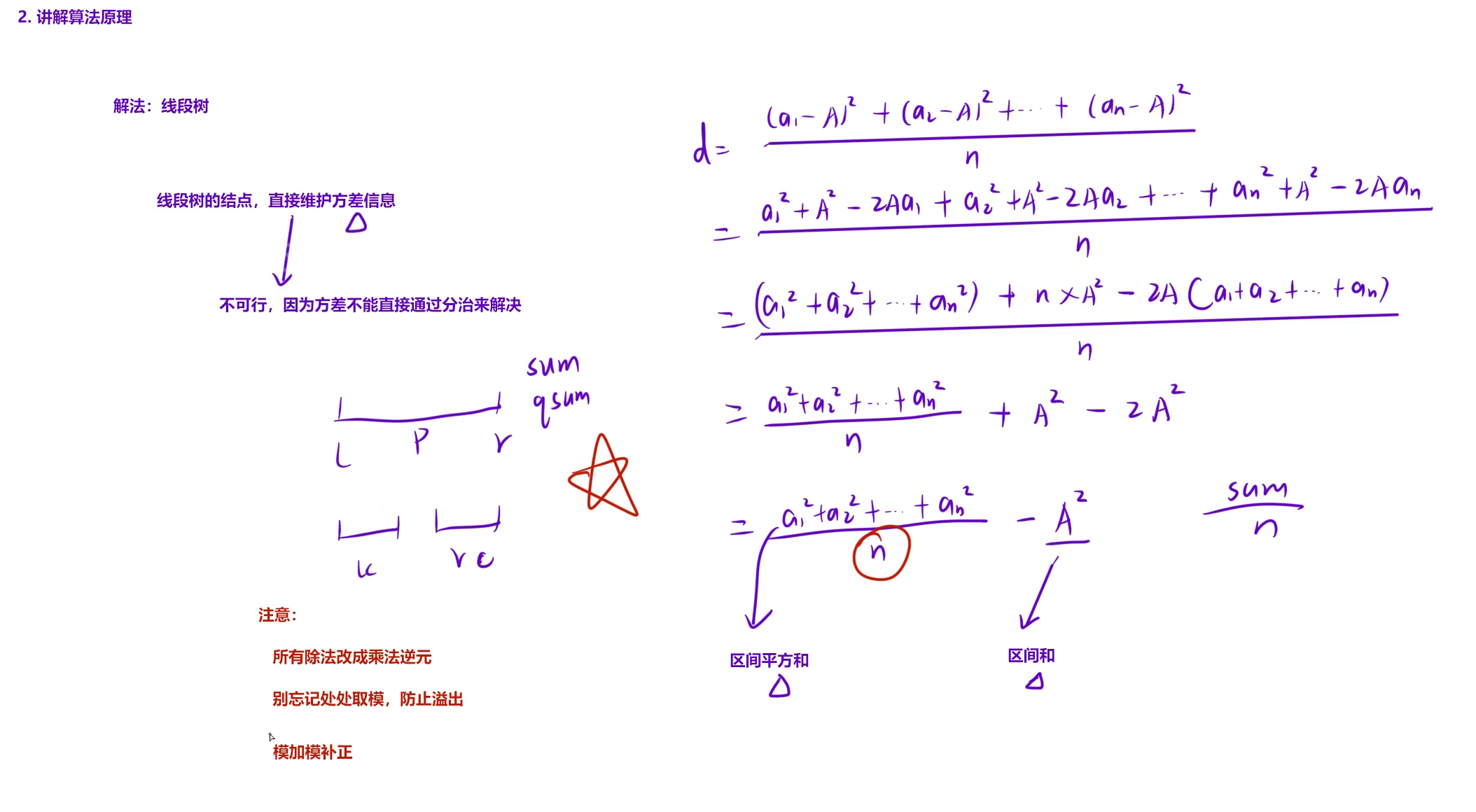
#define lc p<<1
#define rc p<<1|1
const int N = 1e5 + 10, mod = 1e9 + 7;
int n, m;
LL a[N];//很扯淡，这儿必须用LL
struct node 
{
	int l, r;
	LL sum, qsum;
}tr[N<<2];
LL qpow(LL a, LL b, LL p)
{
	LL ret = 1;
	while (b)
	{
		if (b & 1) ret = ret * a % p;
		a = a * a % p;
		b >>= 1;
	}
	return ret;
}
void pushup(node& p, node& l, node& r)
{
	//p.l = l.l, p.r = r.r;
	p.qsum = (l.qsum + r.qsum) % mod;
	p.sum = (l.sum + r.sum) % mod;
}
void build(int p, int l, int r)
{
	tr[p] = { l,r,a[l],a[l] * a[l] % mod };
	if (l == r)return;

	int mid = (l + r) / 2;
	build(lc, l, mid); build(rc, mid + 1, r);
	pushup(tr[p], tr[lc], tr[rc]);
}
void modify(int p, int x, LL y)//将第x个节点的值改为y
{
	int l = tr[p].l, r = tr[p].r;
	if (l == r)
	{
		tr[p].sum = y;
		tr[p].qsum = y * y % mod;
		return;
	}

	int mid = (l + r) / 2;
	if (x <= mid)modify(lc, x, y);
	else modify(rc, x, y);

	pushup(tr[p], tr[lc], tr[rc]);
}
node query(int p, int x, int y)
{
	int l = tr[p].l, r = tr[p].r;
	if (x <= l && y >= r)return tr[p];

	int mid = (l + r) / 2; 
	if (y <= mid)return query(lc, x, y);
	else if (x > mid)return query(rc, x, y);

	node t, L = query(lc, x, y), R = query(rc, x, y);
	pushup(t, L, R);
	return t;
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)cin >> a[i];
	build(1, 1, n);

	while (m--)
	{
		int op, x, y; cin >> op >> x >> y;
		if (op == 1)
		{
			modify(1, x, y);
		}
		else
		{
			node t = query(1, x, y);
			LL sum = t.sum, qsum = t.qsum, len = (y-x+1);
			LL inv = qpow(len, mod - 2, mod);
			LL A = sum * inv % mod;
			LL D = qsum * inv % mod - A * A % mod;
			D = (D % mod + mod) % mod;
			cout << D << endl;
		}
	}
}

P10463 Interval GCD - 洛谷（区间修改（无法懒标记以及剪枝）--利用差分改为单点修改）

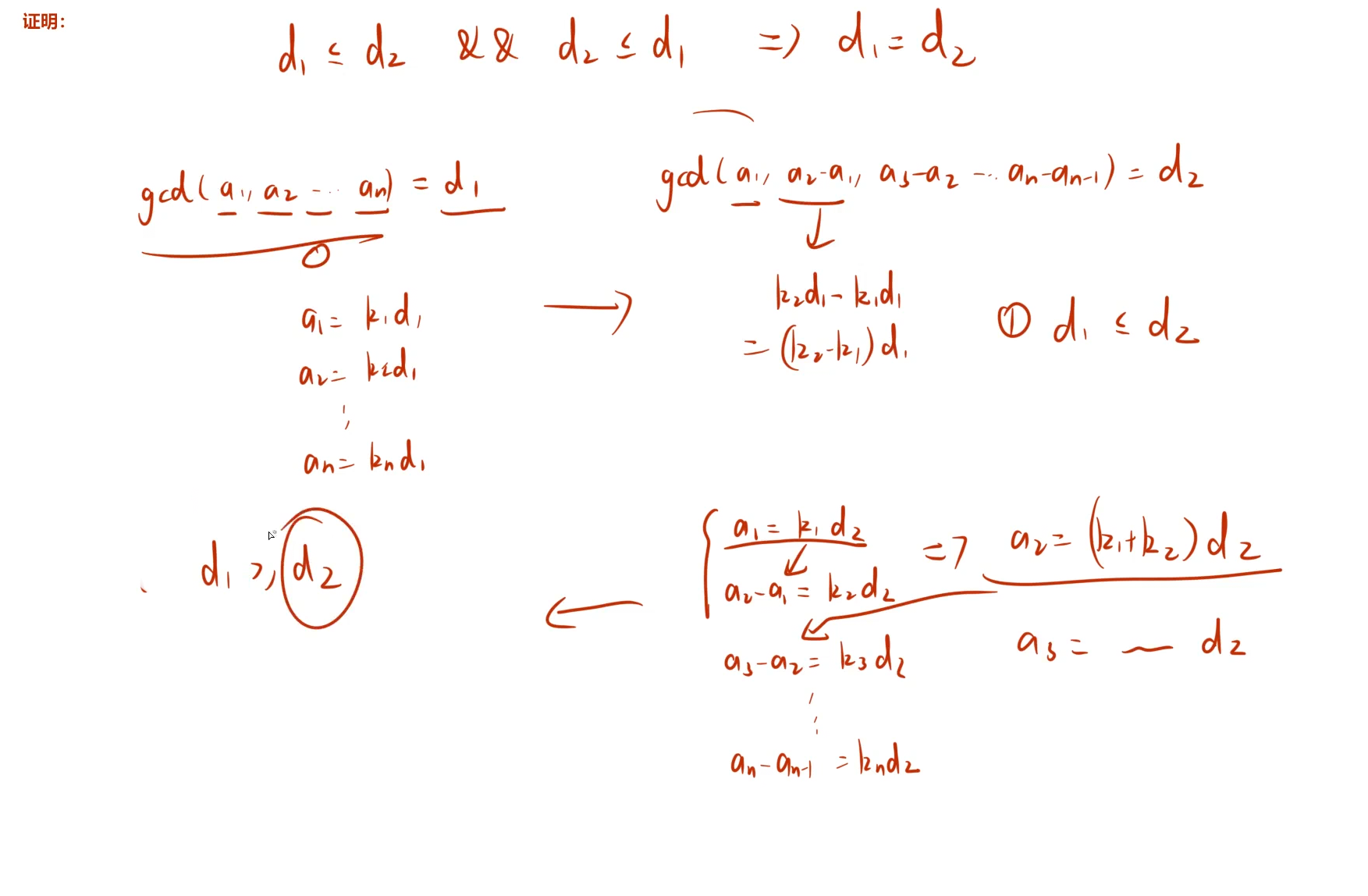
有这个结论，我们就可以维护原序列差分序列中的最大公约数，此时区间修改就变成的两次单点修改.

但是，在求差分序列的最⼤公约数时除了区间的gcd值，还需要知道原数列的值。（可以在差分序列中维护⼀个区间和query1，此时原数列的值就是差分序列中区间的和。

因为gcd区间【l+1,r】和差分和区间【1，l】不同，所以写了两个query，省的返回结构体

注意⽤差分解决问题时，最⼤公约数会出现负数的情况。注意取绝对值

#include<iostream>
using namespace std;
typedef long long LL;
#define lc p<<1
#define rc p<<1|1

const int N = 5e5 + 10;
LL n, m;
struct node
{
	int l, r;
	LL sum, gcd;
}tr[N<<2];
LL gcd(LL a, LL b)
{
	return b == 0 ? a : gcd(b, a % b);
}
LL a[N];//差分数组 注意越界情况
void pushup(int p)
{
	tr[p].sum = tr[lc].sum + tr[rc].sum;
	tr[p].gcd = gcd(tr[lc].gcd, tr[rc].gcd);
}
void build(int p, int l, int r)
{
	tr[p] = { l,r,a[l],a[l] };
	if (l == r)return;

	int mid = (l + r) / 2;
	build(lc, l, mid); build(rc, mid + 1, r);
	pushup(p);
}
void modify(int p, int x, LL k)
{
	int l = tr[p].l, r = tr[p].r;
	if (l == r)
	{
		tr[p].sum += k;
		tr[p].gcd += k;
		return;
	}
	int mid = (l + r) / 2;
	if (x <= mid)modify(lc, x, k);
	else modify(rc, x, k);

	pushup(p);
}
LL query1(int p, int x, int y)
{
	int l = tr[p].l, r = tr[p].r;
	if (x <= l && y >= r)return tr[p].sum;

	int mid = (l + r) / 2; LL ret = 0;
	if (x <= mid)ret += query1(lc, x, y);
	if (y > mid)ret += query1(rc, x, y);

	return ret;

}
LL query2(int p,int x,int y)
{
	int l = tr[p].l, r = tr[p].r;
	if (x <= l && y >= r)return tr[p].gcd;

	int mid = (l + r) / 2; LL g = 0;
	if (x <= mid)g = gcd(query2(lc, x, y),g);
	if (y > mid)g = gcd(query2(rc, x, y), g);

	return g;
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
	{
		LL x; cin >> x;
		a[i] += x; a[i + 1] -= x;
	}
	build(1, 1, n);

	while (m--)
	{
		char ch; cin >> ch;
		if (ch == 'C')
		{
			int l, r; LL d; cin >> l >> r >> d;
			modify(1, l, d);
			if(r+1<=n)modify(1, r + 1, -d);
		}
		else
		{
			int x, y; cin >> x >> y;
			LL sum = query1(1, 1, x);//sum表示第x个元素的值（差分累加值）
			LL g = 0;
			if(x+1<=y) g = query2(1, x + 1, y);
			LL ret = gcd(sum, g);
			cout << abs(ret) << endl;
		}

	}
	return 0;
}