算法——并查集

1. 并查集

1）并查集的概念

• 并查集: 即“不相交集合”（Disjoint Set），是一种数据结构。对于这种数据结构，最常见的两种操作是合并和查找。
• 合并: 将两个集合合并成一个集合。
• 查找: 查找某个元素属于哪个集合。
• 实现方式: 通常用1到n来表示n个对象，以方便进行并查集的操作。

2）并查集的实现方式

• 第一种实现方式: （此处先提及，后续会详细讲解）
• 注意: 虽然会讲两种实现方式，但一般使用第二种，第一种也会进行简单介绍。

2. 实现方法

1）方法一

• 用编号最小的元素标记所在集合
  • 定义与实现方法
    • 定义: 用编号最小的元素标记所在集合，即每个集合用其最小元素作为代表。
      • 这里的 Set 是一个数组，其中：
      • 下标 x：代表 “元素 x” 本身（比如 Set[8] 中的 8 就是元素 8）。
      • 值 Set[x]：代表 “元素 x 所属集合的标识”（通常是集合中 “编号最小的元素”，也称为 “集合的代表元”）。
    • 实现方法: 定义一个数组Set[1……n]，其中Set[i]表示元素i所在的集合，就是已经知道元素所在集合，然后在这里面找出最小的，再定义一个set数组，把他们存储进去
    • 示例:
      • 如{1,3,7}，{4}，{2,5,9,10}，{6,8}，其中Set[1] = Set[3] = Set[7] = 1，表示元素 1, 3, 7 都在以 1 为代表的集合中。
      •  如Set[8] = 6，意思是：元素 8 所属的集合，是 “以 6 为代表元的集合”
  • 不相交集合的概念
    • 不相交集合: 任意两个集合的交集为空，即一个元素只能属于一个集合。
    • 举例: 如上例中的四个集合，每个元素只出现在一个集合中，满足不相交集合的定义。
  • 用编号最小的元素代表集合
    • 目的: 简化集合的表示，方便查找和合并操作。
    • 类比: 类似于班级中的班长，用班长代表整个班级，集合中的最小元素代表整个集合。
    • 举例: 集合{2,5,9,10}中，元素 2 作为最小元素，代表该集合。
  • 集合的查找操作
    • 查找操作: 查找元素

      xxx

      所属的集合，即返回Set[x]。
      • 查找 “元素 x 所属的集合” 时，直接返回 Set[x]，是因为 Set[x] 本身就存储了 “x 所属集合的标识”。
      • 所以，程序不需要 “额外计算”，直接通过数组下标访问 Set[x]，就能得到 x 所属集合的标识 —— 这就是 “查找时间复杂度 O(1)” 的原因（数组随机访问是 O(1)）。
    • 效率: 查找操作的时间复杂度为 O(1)，因为直接通过数组下标访问。
    • 示例: 查找元素 8 所属的集合，返回Set[8] = 6，表示元素 8 在以 6 为代表的集合中。
• 方法一效率分析
  • 查找操作效率: 查找操作非常高效，时间复杂度为O(1)。
  • 合并操作效率: 合并操作需要遍历整个数组，时间复杂度为O(n)，其中n是数组的长度。
  • 合并操作实现: 合并两个集合时，需要将一个集合中的所有元素重新指向另一个集合的代表元素。例如，合并集合{6,8}和{2,5,9,10}，需要将Set[6]和Set[8]的值改为 2。
  • 问题: 当数组元素非常多时，合并操作会变得非常慢，因为需要遍历整个数组。
  • 改进思路: 考虑使用树状结构来优化合并操作，减少遍历元素的数量。

2）方法二

• 避免最坏情况
  • 合并策略：当合并两棵树时，选择高度更高的树作为合并后的根节点（"老大"），这样可以避免合并后树的高度增加。
  • 高度记录：需要记录每棵树的高度信息，合并时比较两棵树的高度。
  • 效果说明：通过这种优化，可以确保包含k个节点的树的最大高度不超过lgk，将最坏情况的时间复杂度改进到对数级别。
  • 完整流程操作：
    • 初始化 init：
      • 每个元素初始时 “自己是自己的父节点”（Set[i] = i），树的高度为 1（height[i] = 1）。
    • 查找 find（带路径压缩）：
      • 递归找到根节点，并把路径上所有节点的父节点直接指向根（路径压缩），让后续查找更快。
    • 合并 merge（按秩合并）：
      • 先找到两个元素的根节点 rootA 和 rootB。
        • 若根相同，说明已在同一集合，直接返回。
        • 若根不同，比较两棵树的高度：
          • 高度相同：把其中一个根的父设为另一个根，且被合并的根的高度 +1。
          • 高度不同：把高度低的根的父设为高度高的根，高度高的根的高度不变。
  • 算法实现：
    • 当两棵树高度相等时：合并后高度增加1，

      h=h1+1h = h1 + 1h=h1+1

    • 当两棵树高度不等时：合并后高度取两者最大值，

      h=max⁡(h1,h2)h = \max(h1, h2)h=max(h1,h2)

  • 代码实现：

#include <stdio.h>
#include <stdlib.h>

#define MAX_N 100  // 假设最多有100个元素

// Set数组：Set[x]表示x的父节点；height数组：height[x]表示以x为根的树的高度
int Set[MAX_N];
int height[MAX_N];

// 初始化：每个元素自己为一个集合（父节点是自己，高度为1）
void init(int n) {
    for (int i = 0; i < n; i++) {
        Set[i] = i;
        height[i] = 1;
    }
}

// 查找操作（带路径压缩，进一步优化查找效率，这里也加上，让整体更高效）
int find(int x) {
    if (Set[x] != x) {
        // 路径压缩：把x的父节点直接指向根节点
        Set[x] = find(Set[x]);
    }
    return Set[x];
}

// 合并操作（按秩合并）
void merge(int a, int b) {
    int rootA = find(a);
    int rootB = find(b);
    if (rootA == rootB) return;  // 已经在同一集合，无需合并

    if (height[rootA] == height[rootB]) {
        // 高度相同，合并后高度+1
        Set[rootA] = rootB;
        height[rootB]++;
    } else if (height[rootA] < height[rootB]) {
        // A的树更矮，把A合并到B下，B的高度不变
        Set[rootA] = rootB;
    } else {
        // B的树更矮，把B合并到A下，A的高度不变
        Set[rootB] = rootA;
    }
}

int main() {
    int n = 10;  // 假设元素是0~9
    init(n);

    // 示例：合并集合
    merge(0, 1);   // 合并{0}和{1} → 集合{0,1}（根为1，height[1]=2）
    merge(2, 3);   // 合并{2}和{3} → 集合{2,3}（根为3，height[3]=2）
    merge(0, 2);   // 合并{0,1}和{2,3}：
                   // rootA是find(0)=1（height[1]=2），rootB是find(2)=3（height[3]=2）
                   // 高度相同，合并后rootB（3）的高度+1 → height[3]=3，Set[1]=3
    merge(4, 5);   // 合并{4}和{5} → 集合{4,5}（根为5，height[5]=2）
    merge(6, 7);   // 合并{6}和{7} → 集合{6,7}（根为7，height[7]=2）
    merge(4, 6);   // 合并{4,5}和{6,7}：
                   // rootA是find(4)=5（height[5]=2），rootB是find(6)=7（height[7]=2）
                   // 高度相同，合并后rootB（7）的高度+1 → height[7]=3，Set[5]=7

    // 查找每个元素的根，验证合并结果
    for (int i = 0; i < 8; i++) {
        printf("元素%d的根是：%d\n", i, find(i));
    }
    return 0;
}

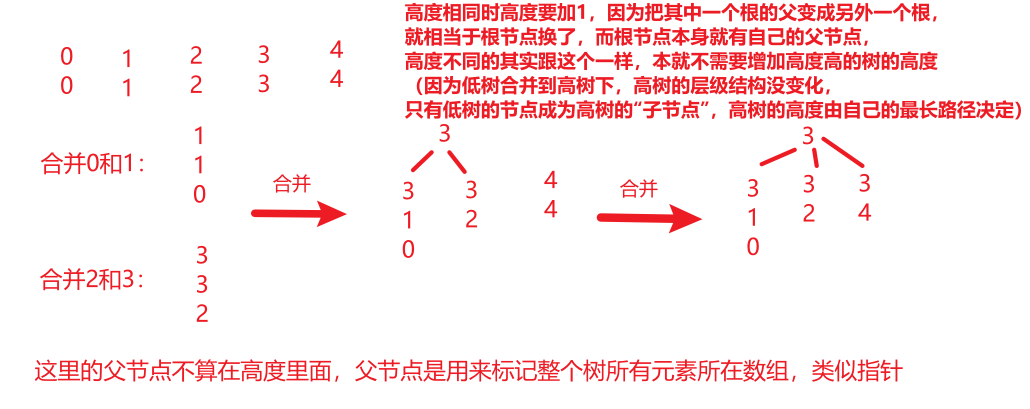
• 案例具体分析：
  • 初始状态（每个元素自成一棵树）
    • 假设元素是 0,1,2,3，初始时：
    • Set[i] = i（每个元素的父节点是自己）。
    • height[i] = 1（每棵树只有 1 个节点，高度为 1）。
    • 图示（每个方框代表一个节点，箭头指向父节点）：

0 → 0   1 → 1   2 → 2   3 → 3

• 合并操作 1：merge(0, 1)
  • 找根：find(0) 得到 0，find(1) 得到 1。
  • 比较高度：height[0] = height[1] = 1（高度相同）。
  • 合并规则：把其中一个根的父设为另一个根，且被合并的根的高度 +1。这里选择 Set[0] = 1，并将 height[1] 改为 2。

0 → 1 → 1   2 → 2   3 → 3

（解释：0 的父是 1，1 是自己的父；2、3 仍自成树。此时以 1 为根的树高度为 2，包含节点 0 和 1。）

• 合并操作 2：merge(2, 3)
  • 合并规则：选择 Set[2] = 3，并将 height[3] 改为 2。
  • 比较高度：height[2] = height[3] = 1（高度相同）。
  • 找根：find(2) 得到 2，find(3) 得到 3。

0 → 1 → 1   2 → 3 → 3

（解释：2 的父是 3，3 是自己的父；0、1 所在树不变。此时以 3 为根的树高度为 2，包含节点 2 和 3。）

• 合并操作 3：merge(0, 2)
  • 合并规则：选择 Set[1] = 3，并将 height[3] 改为 3。
  • 比较高度：height[1] = 2，height[3] = 2（高度相同）。
  • 找根：find(0) 会递归找到根 1（因为 0→1→1）；find(2) 会递归找到根 3（因为 2→3→3）。

0 → 1 → 3 → 3   2 → 3 → 3

（解释：1 的父是 3，0 的父是 1；2 的父是 3；3 是自己的父。此时以 3 为根的树高度为 3，包含节点 0,1,2,3。）

• 合并操作 4：merge(0, 3)（验证 “高度不同时的合并”）
  • 合并规则：把高度低的根（4）的父设为高度高的根（3），高度高的根（3）的高度不变。即 Set[4] = 3，height[3] 仍为 3。
  • 比较高度：height[3] = 3 > height[4] = 1（高度不同）。
  • 找根：find(0) 得到 3（height[3]=3）；find(4) 得到 4（height[4]=1）。
  • 假设现在要合并 0 和 3，但此时 0 的根是 3（同一集合，无需合并）。我们换一个例子：合并 0 和 新元素 4（初始 Set[4]=4，height[4]=1）。

0 → 1 → 3 → 3   2 → 3 → 3   4 → 3 → 3

（解释：4 的父是 3；3 的高度仍为 3，因为是 “低的合并到高的下”，高的树的高度不会增加。）

• 图解：

• 实际应用：
  • 实现提醒：虽然这种优化理论上可以避免最坏情况，但在实际比赛和编程中很少需要实现，因为基础实现通常已经足够高效。
  • 查找算法：查找算法的代码保持不变，但通过高度优化后，最坏情况时间复杂度已改进到对数级别。

3. 应用案例

1）例题:城镇道路连接

• 题目背景

• 背景描述: 某省调查城镇交通状况，目标是使全省任何两个城镇间都可以实现交通。
• 问题: 问最少还需要建设多少条道路？
• 题目解析
  • 问题转化
    • 问题本质: 要使n个城镇互联互通，最少还需建设多少条道路，实质是求集合数量减一。
    • 并查集应用: 使用并查集处理连通性问题，合并集合，最终集合数量减一即为答案。
  • 代码解析
    • 输入格式: 首先读入n（城市数）和m（道路数），数据以0结束。
    • 初始化: 每个人（城市）最初都是自己的老大（独立集合）。
    • 合并操作: 每读入一条道路，合并两个城市所在的集合。
    • 查找老大: 使用findx函数找到元素所在集合的老大。
    • 合并条件: 如果两个元素的老大不同，则合并这两个集合。
    • 统计集合数量: 最终统计老大的数量，即集合数量，减一即为还需建设的道路数。
  • 代码实现细节
    • 输入结束条件: 使用while(scanf("%d", &n), n)判断输入是否结束，n为0时结束。
    • 初始化: for循环初始化每个人为自己的老大，bin[i] = i。
    • 合并函数: merge函数实现集合合并，findx函数找到元素的老大。
    • 统计集合数量: 最后遍历所有元素，统计老大的数量，即集合数量。
  • 学习建议
    • 理解代码: 真正理解代码逻辑，而不是照抄模板。
    • 负责每一行代码: 为自己写的每一行代码负责，不理解的不写。
    • 发现问题: 通过自己实现发现问题，再去找问题，加深记忆。

疑惑：这里想到顶点连通性可能会想到之前的青蛙邻居，判断是否可图化

我们可以先来分析一下为什么用并查集，然后再来分析他们的区别

一、“城镇道路连接” 用并查集的原因

• 题目要让 “所有城镇互通”，即最终只有1 个连通分量（所有城镇在同一个集合里）。
• 并查集的核心能力是：
  • 高效管理 “不相交集合”，支持合并集合（将连通的城镇合并到同一集合）和查找集合代表元（判断城镇是否已连通）。
• 解题逻辑：
  • 初始时，每个城镇是独立的集合（共 n 个集合）。
  • 对于已有道路连通的城镇，用并查集合并它们的集合。
  • 最终，若有 k 个连通分量（即并查集中有 k 个不同的根），则需要新建 k−1 条道路（把 k 个集合连成 1 个，需要 k−1 条边）。

二、与 “青蛙邻居（可图化）” 的异同

• 1. 相同点：都涉及 “集合 / 连通性”
  • 并查集处理 “城镇的连通集合”，合并的是城镇（顶点）的连通关系。
  • Havel - Hakimi 定理处理 “青蛙邻居的度数序列”，判断的是顶点度数是否能构成合法的图（连通或非连通）。
  • 两者都围绕 “顶点的连接关系” 展开，但目标和方法完全不同。
• 2. 不同点：问题目标与方法

三、是否有 “类似青蛙问题” 的方法？

• 如果强行想模仿 “青蛙问题的 Havel - Hakimi 定理”，思路会很牵强，因为两者的问题场景完全不同：
  • 青蛙问题是 “给定度数，判断能否成图”，需要模拟顶点连边的过程（排序→删数→减度）。
  • 城镇问题是 “给定部分连通关系，求最少边让全连通”，需要直接管理连通集合的数量。
• 但从 “逐步合并 / 构造” 的角度，能找到一点微弱的联系：
  • 并查集的 “合并集合”，类似于 Havel - Hakimi 中 “顶点连边（合并两个顶点的邻居关系）”。
  • 最终 “集合数 k−1”，类似于 Havel - Hakimi 中 “最终全为 0（成功构造图）” 的 “终止条件”。
• 但这种联系很表面，因为：
  • 并查集是直接管理集合，操作简单（合并、查找）。
  • Havel - Hakimi 是模拟连边的规则，操作复杂（排序、删数、减度、判断负数）。

总结：“城镇道路连接” 用并查集是因为问题本质是 “连通分量的数量统计”，并查集是最直接高效的工具。它和 “青蛙邻居” 的可图化问题虽都涉及 “顶点连接”，但目标、方法、逻辑本质差异很大，无法用完全类似的方法解决。

• 并查集的应用与理解
  • 并查集的优势: 在处理连通性问题时非常方便，如最小生成树等算法中常用。
  • 形象易懂: 并查集相对形象易懂，是数据结构中非常有用的工具。

2）例题:迷宫判断

• 题目要求
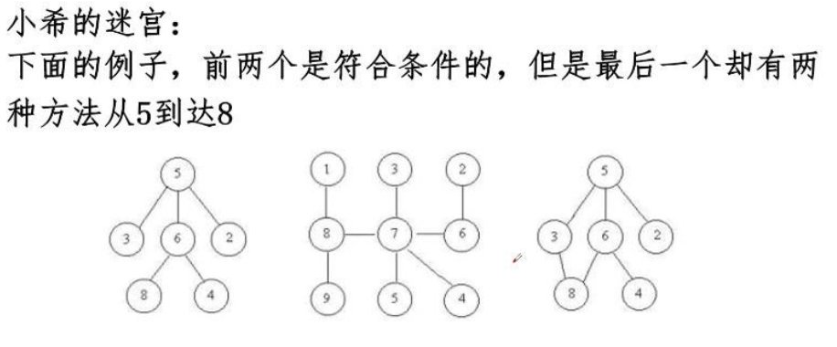
  • 连通性要求：任何两个房间之间必须有且只有一条通路
  • 禁止条件：图中不能出现回路（环）
  • 示例说明：前两个示例符合要求，最后一个示例中5到8有两条路径（5-3-6-8和5-4-8），因此不符合要求
• 解题方法
  • 并查集解法
    • 判断条件：
      • 唯一根节点：最终所有节点必须属于同一个集合（只有一个"老大"）
      • 无环检测：每次添加边时检查两个顶点是否已连通，若已连通则说明形成环
    • 实现步骤：
      • 初始化并查集
      • 遍历所有边，对每条边执行：
        • 检查两个顶点是否已连通
        • 若已连通则直接判定不符合要求
        • 否则合并两个集合
      • 最后检查是否所有节点属于同一集合

3）例题:最小生成树

• 基本概念
  • 图定义：由顶点和边组成的数据结构，每条边连接两个顶点
  • 树定义：具有n个顶点、n-1条边且连通的图
  • 生成树：包含原图所有顶点和部分边（n-1条）的树状子图
  • 最小生成树：所有生成树中边权值之和最小的生成树
• 应用实例
  • 问题背景：6个岛屿需要修建桥梁实现互通，有12个可选建桥方案
  • 优化目标：选择总造价最低的建桥方案（15亿方案优于21亿方案）
  • 算法价值：实际决策中可节省大量成本
• Kruskal算法
  • MST性质
    • 定义：Kruskal 算法是求解 MST 的经典贪心算法，核心思路是 “优先选短边，避免成环”，依赖并查集（Union-Find） 维护顶点连通性。
    • 核心定理：任何连通图至少存在一棵最小生成树包含最短边
    • 证明方法：反证法（假设不包含最短边可构造更小生成树，导致矛盾）
  • 算法步骤
    • 设图中有n个顶点、m条边：
    • 边排序：将所有边按权值从小到大（升序）排序。
    • 初始化并查集：每个顶点独立成为一个集合（表示初始时所有顶点均不连通）。
    • 筛选有效边：按排序后的顺序遍历每条边，对当前边(u,v,w)：
      • 用并查集检查u和v是否在同一集合（即是否已连通）。
      • 若不连通：将u和v所在集合合并，同时将该边加入 MST 的边集，累计总权值。
      • 若已连通：跳过该边（加入会形成环，违反树的无环性质）。
    • 终止条件：当 MST 的边集已包含n−1条边时，停止遍历（此时已连通所有顶点，无需处理剩余边）。
  • 具体演示过程：
    • 初始并查集：{1},{2},{3},{4},{5},{6}，MST 边数 = 0，总造价 = 0。
    • 处理边 1-3（权 1）：1 和 3 不连通，合并为{1,3}，MST 边数 = 1，总造价 = 1。
    • 处理边 4-6（权 2）：4 和 6 不连通，合并为{4,6}，MST 边数 = 2，总造价 = 1+2=3。
    • 处理边 2-5（权 3）：2 和 5 不连通，合并为{2,5}，MST 边数 = 3，总造价 = 3+3=6。
    • 处理边 3-6（权 4）：3（属{1,3}）和 6（属{4,6}）不连通，合并为{1,3,4,6}，MST 边数 = 4，总造价 = 6+4=10。
    • 处理边 3-4（权 5）：3 和 4 已在同一集合（{1,3,4,6}），跳过。
    • 处理边 1-4（权 6）：1 和 4 已在同一集合，跳过。
    • 处理边 2-3（权 5）：2（属{2,5}）和 3（属{1,3,4,6}）不连通，合并为全集，MST 边数 = 5（n−1=6−1=5），总造价 = 10+5=15。
    • 终止：MST 构造完成，总造价 15 亿（最优方案）。
  • 实现技巧：边的存储：用结构体数组存储边信息，结构体包含 3 个字段：起点u、终点v、权值w（示例：struct Edge {int u, v, w;}）。
    • 边的排序：调用排序函数（如 C++ 的sort），自定义比较规则（按w升序）。
    • 并查集实现：核心是两个函数：
      • find(x)：查找顶点x所在集合的 “根节点”（带路径压缩优化，减少后续查找时间）。
      • union(x,y)：将顶点x和y所在集合合并（按秩 / 大小合并优化，避免树退化为链）。

4）例题:道路总长最小

• 题目描述
  • 问题描述：n个城市需要修建道路实现两两互通，有m种可选道路方案（三元组(u,v,w)）
  • 优化目标：选择总长度最小的道路建设方案
  • 问题本质：标准的最小生成树问题
• 解题要点：
  • 步骤 1：明确输入输出与数据结构
    • 输入：城市数量n，可选道路数量m，m个三元组(u,v,w)（注意：城市编号通常从 1 或 0 开始，需统一处理）。
    • 输出：道路总长度的最小值（即 MST 的总权值）。
    • 核心数据结构：
      • 结构体数组edges[]：存储所有道路的u,v,w。
      • 并查集数组parent[]：维护城市的连通关系，parent[x]表示城市x的父节点。
  • 步骤 2：实现并查集（关键工具）

// 查找根节点（带路径压缩）
int find(int x, int parent[]) {
    if (parent[x] != x) {
        parent[x] = find(parent[x], parent); // 路径压缩：让x直接指向根节点
    }
    return parent[x];
}

// 合并两个集合（按秩合并，可选优化）
void unionSet(int x, int y, int parent[], int rank[]) {
    int rootX = find(x, parent);
    int rootY = find(y, parent);
    if (rootX != rootY) {
        // 秩小的树合并到秩大的树，避免树过高
        if (rank[rootX] > rank[rootY]) {
            parent[rootY] = rootX;
        } else if (rank[rootX] < rank[rootY]) {
            parent[rootX] = rootY;
        } else {
            parent[rootY] = rootX;
            rank[rootX]++; // 秩相等时，合并后根的秩+1
        }
    }
}

• • 步骤3：按 Kruskal 算法核心流程解题
    • 输入处理与初始化：
      • 读取n和m，若n=1（只有 1 个城市），直接输出 0（无需修道路）。
      • 读取m条道路，存入edges[]数组。
    • 初始化并查集：parent[i] = i（每个城市自己是根节点），rank[i] = 0（初始秩为 0）。
    • 边排序：调用sort函数，按道路长度w升序排序edges[]。
    • 筛选有效边并计算总长度：
      • 初始化变量：total_len = 0（总长度），count = 0（已选道路数量）。
      • 遍历排序后的每条边：
        • 取当前边的u,v,w，调用find(u)和find(v)，判断是否连通。
          • 若不连通：
          • total_len += w（累加长度）。
          • unionSet(u, v, parent, rank)（合并集合）。
          • count++（已选道路数 + 1）。
          • 若count == n-1（已选够n−1条边），立即跳出循环（无需处理剩余边）。
    • 结果输出：
      • 若count == n-1：输出total_len（成功构造 MST，总长度最小）。
      • 若count < n-1：输出 “无法连通所有城市”（原图不连通，无生成树）。
• 步骤 4：解题关键注意事项
  • 边界情况处理：
    • 当n=1时，总长度为 0（无道路需求）。
    • 当m<n−1时，必然无法连通所有城市（边数不足，树至少需n−1条边）。
  • 数据范围：道路长度w可能较大，需用合适的数据类型（如long long）存储total_len，避免溢出。
  • 并查集优化：路径压缩和按秩合并必须实现，否则在n和m较大时（如1e5级别），时间复杂度会过高（从O(mlogm)退化到O(mn)）。
• 示例代码（C++）

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

struct Edge {
    int u, v, w;
    // 排序规则：按权值升序
    bool operator<(const Edge& other) const {
        return w < other.w;
    }
};

int find(int x, vector<int>& parent) {
    if (parent[x] != x) {
        parent[x] = find(parent[x], parent);
    }
    return parent[x];
}

void unionSet(int x, int y, vector<int>& parent, vector<int>& rank) {
    int rootX = find(x, parent);
    int rootY = find(y, parent);
    if (rootX != rootY) {
        if (rank[rootX] > rank[rootY]) {
            parent[rootY] = rootX;
        } else if (rank[rootX] < rank[rootY]) {
            parent[rootX] = rootY;
        } else {
            parent[rootY] = rootX;
            rank[rootX]++;
        }
    }
}

int main() {
    int n, m;
    cin >> n >> m;
    if (n == 1) {
        cout << 0 << endl;
        return 0;
    }
    vector<Edge> edges(m);
    for (int i = 0; i < m; i++) {
        cin >> edges[i].u >> edges[i].v >> edges[i].w;
    }
    // 初始化并查集
    vector<int> parent(n + 1); // 假设城市编号1~n
    vector<int> rank(n + 1, 0);
    for (int i = 1; i <= n; i++) {
        parent[i] = i;
    }
    // 排序边
    sort(edges.begin(), edges.end());
    // 筛选边
    int total_len = 0;
    int count = 0;
    for (auto& e : edges) {
        int u = e.u, v = e.v, w = e.w;
        int rootU = find(u, parent);
        int rootV = find(v, parent);
        if (rootU != rootV) {
            total_len += w;
            unionSet(u, v, parent, rank);
            count++;
            if (count == n - 1) {
                break;
            }
        }
    }
    // 输出结果
    if (count == n - 1) {
        cout << total_len << endl;
    } else {
        cout << "无法连通所有城市" << endl;
    }
    return 0;
}