电容的作用, 电容的物理基础 : 信号与电源完整性_深沟槽电容对信号完整性和电源完整性的影响-CSDN博客

本文链接：https://blog.csdn.net/2401_87854160/article/details/147009912

电容的符号如图2-23所示。

图2-23　电容的符号　

电容是一个储存电荷的容器，电容的容值代表着其储存电荷的能力，对电容容值的定义式为

其中，C是电容的容值，单位是法拉（F）；Q是电量，单位是库伦（C）；U 是电压，单位是伏特（V）。

这意味着同样的电压下，电容容值越大，能够储存的电荷就越多。

同样，上面只是一个电容容值的定义式，对于一个电容器来说，其电容的大小跟电压和电量都没有关系，而是与它本身的结构有关。以我们熟悉的平板电容举例，其容值的大小为

其中，ε0为自由空间介电常数，约为0.089 pF/cm（0.225pF/in）；εr为平板之间介质的介电常数（常常会写成Er），就是一个系数，表示其与自由空间介电常数的比值，没有单位；S为平板的正对面积，单位是m^2；d为平板之间的间距，单位是m。

电容是我们理解信号完整性现象非常重要的一个部分，在式（2-3）中，我们可以看到：介电常数越大，电容越大；平板的正对面积越大，电容越大；平板之间的间距越近，电容越大。实际上我们平板电容的容值有多大呢？按照我们常见的参数来看，FR-4板材，4mil的芯板，平面的大小为

电容器也有阻抗这个概念，同样由欧姆定理得出。

由C=Q /U可以看出，当电压变化时，电容两端的电量也会发生变化。这样我们就会得到以下公式为

这个电流并不是直接流过电容器的，而是当电容器两端的电压变化时，电容会重新充、放电，看起来好像有电流流过一样。同时，流过的电流大小跟电压大小没关系，只跟电压变化的快慢有关。根据式（2-4），我们稍做变形就能得到电容器的阻抗为

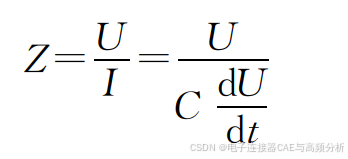
式（2-5）中可以看到，阻抗Z跟电压变化的速率有关。这是一个带有时间t的公式，也就是我们所说的时域中的阻抗。不过一条时域的曲线是无法描述电容的阻抗，它不仅跟时间的变化有关，同时也跟电压的变化有关。所以至少要加上一个电压随时间变化的曲线，才可以得到电容的阻抗随着时间变化的关系。

这也是前面所说的时域的局限性，因为时域是现实生活中存在的，人们非常好理解，但是在处理高频高速的现象时，时域难以描述一些现象。

我们切换至频域中，看看频域中电容的阻抗是什么样子。

时域中的阻抗公式，描述的难点在于需要同时描述一个电压随时间变化的曲线，但是在频域中，正弦波是唯一存在的波形。电压U的时域表达式变为了Usin（2πf×t）或者Usin（ωt），其关于t的导数为U×2πf×cos（2πf×t）或者U×ω×cos（ωt），于是式（2-5）变为

可以看到，理想电容的阻抗随着频率的升高而变小。也就是我们平时所说的通交流，阻直流。理想电容的阻抗特性如图2-24所示