Abaqus的线弹性与塑性:
線 彈 性:
•
大多數的材料在某些變形範圍內都保有彈性。
•
如延性材料,彈性行為的範圍非常有限。
•
一個線彈性材料的模型:
•
在微小彈性應變下,是有效的
(
通常小於
5
%
)
;
•
可以為等向性、正交性或是完全不等向性;
•
可以具有隨溫度或場域變數改變的性質。
•
正交性與非等向性的材料定義需要使用局部的材料方向。
•
線彈性材料的虎克定律:
stress ∝ strain.
•
虎克定律的一般氏寫為



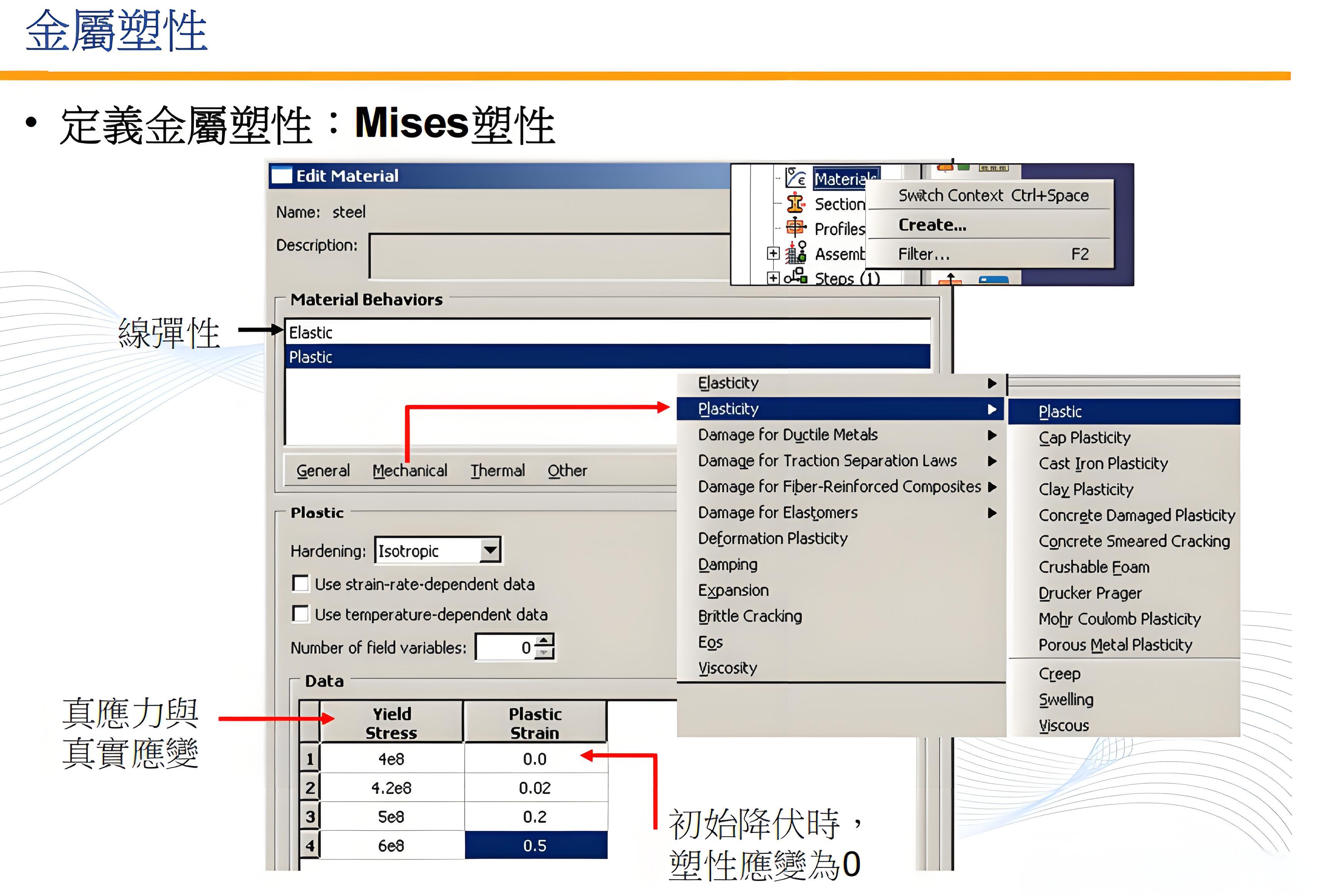
金 屬 塑 性:
•
彈塑性實體金屬的典型單軸應力應變曲線如下所示:

• 承受載重時,多數金屬在達到降伏點之前,幾乎是線彈性行為。
•
如果金屬內的應力超過降伏應力,多數金屬會有塑性變形。
•
多數的材料,降伏應力的數值只佔彈性模數的一小部分,通常是
0.1-1%
。 因此金屬的彈性應變從不會超過這個範圍。
•
因此,金屬的彈性行為可以被模擬成線性。
• Abaqus
中,所有的金屬塑性模型都搭配線彈性的行為。
•
降伏時,模數會有顯著的改變。
•
如果材料變形超過降伏點,而卸載,材料會依楊氏模數的斜率回復變形。
•
註 解:
金屬塑性會在“Metal Inelasticity in Abaqus”中進一步討論。
• 降 伏 面
• Abaqus
裡,可使用
Mises(
等向性
)
與
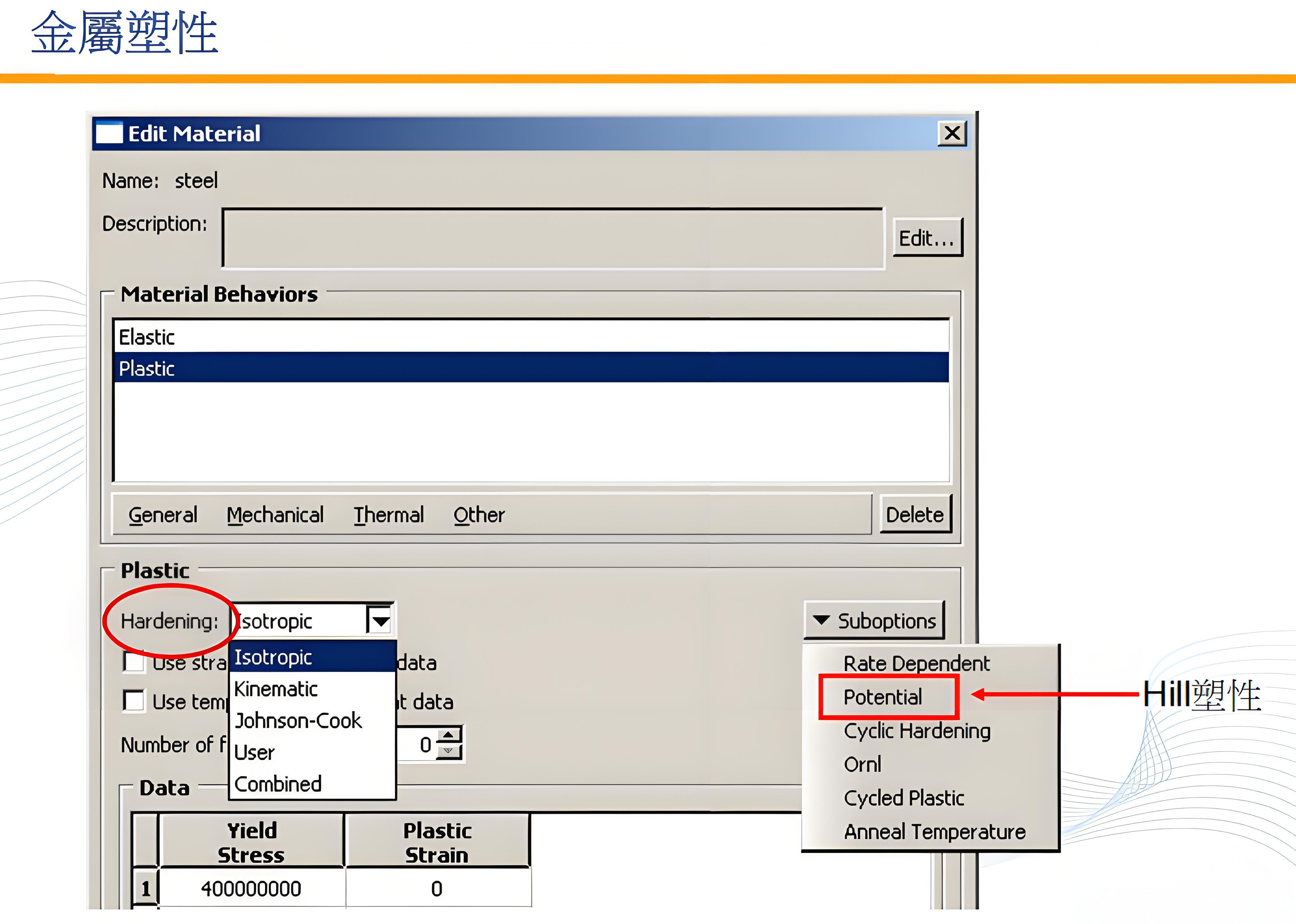
Hill(
非等向性
)
降伏準則。
• Mises
塑性是用來針對金屬的初始等向性降伏行為。
•
適用於金屬承受單純的載重
(
例如,碰撞分析與成形模擬
)
。
• Hill
塑性是用來針對金屬的初始非等向性降伏行為
(
例如,因冷加工所 致).
•
模型假設非等向性不介入材料的塑性變形。
•
只能被用在應變小於
5
%
。



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








