深度学习入门解析

causaliy

已于 2024-10-16 11:13:40 修改

阅读量1.6k

点赞数 48

文章标签：深度学习人工智能

于 2024-08-09 13:49:03 首次发布

本文链接：https://blog.csdn.net/2402_83372966/article/details/140781936

版权

于24年7月15号晚提书学习，提笔于7月29号晚10点，8月9号落笔结题，后续可能还会有时修改。全程26天，体验过各种心理历程和情绪变化，这也是一种奇特的体验，但总归写完了。

在正式开始前，请容许我引用一段我喜欢的诗词。语文，失去了高中过渡的作用后，便是那么的文雅。

滕王阁序

【唐】王勃

天高地迥，觉宇宙之无穷；兴尽悲来，识盈虚之有数。

望长安于日下，目吴会于云间。

地势极而南溟深，天柱高而北辰远。

关山难越，谁悲失路之人；萍水相逢，尽是他乡之客。

我还是那么喜欢手抄知识点，也就有了本博客的产生，是习惯使然也是熟读该书的必然。还是喜欢将我的成果分享给大家。接下来我会按照该书大题框架给出解析，由于能力受限并无更多延申，本博客可以帮助你更好入门理解。

所识甚少，所学甚寡，不足为外人道也，若有不足之处还请见谅，毕竟第一次写这个。

第1章深度学习入门浅谈

自从2012年ILSVRC（大规模图像识别大赛）比赛后，深度学习便一直活跃在学术上。而本篇博客将会展开对深度学习入门的电子解析，内容基于《深度学习入门：基于python的理论与实现》。

整本书大致内容也不过是对神经网络各层次进行介绍，比如激活函数的介绍和使用，参数的介绍使用和最优化，以及方向传播优化算法等。

学习前可以重温一下数分的偏导和梯度和线代的矩阵。

第2章神经网络

2.1 感知机是什么

对于陌生的感知机，我想大家可能会对逻辑电路中的与或非门更为理解，跟计算机相同，计算机是由无数与非门的结合便能实现计算机的处理能力，而神经网络也是由众多的感知机组成。

感知机会接受多个输入信号，输出一个信号。在众多的输入信号中，多会有一个与其对应的权重，或者说是这个数据的分量占比（权重越大越能说明该信号的重要性）。而感知机会整合所有输入信号与对应的权重乘积的和，然后加上偏置b，函数为 $eq?y%3D%5Comega%201%20x1+%5Comega%202%20x2%20+b$ 。当然输入信号的数量也不会止于两个。

下面是感知机公式的代码例子实现

import numpy as np
x=np.array([0.5,1])     #输入信号
w=np.array([0.5,0.7])   #权重
b=-0.2                  #偏置
y=x*w                   #相同结构的数组，对应位置的数相乘。而b会加到数组内所有数上
  #x*w为[0.25,0.7]
y=np.sum(y)+b           #np.sum计算数组总和   
y

2.2 从感知机到神经网络

即便是复杂的问题，感知机理论上也可以将其表示出来。而围绕神经网络，不得不提及感知机的权重与偏置，神经网络的学习目的也是为了寻找合适的权重与偏置。

神经网络顾名思义是模仿大脑神经的运行模式，大脑中的信号传递会一层层流经神经元，在几千万乃至更多的层数上诞生了人类强大的思考计算能力。而下面将举例一个三层神经元网络

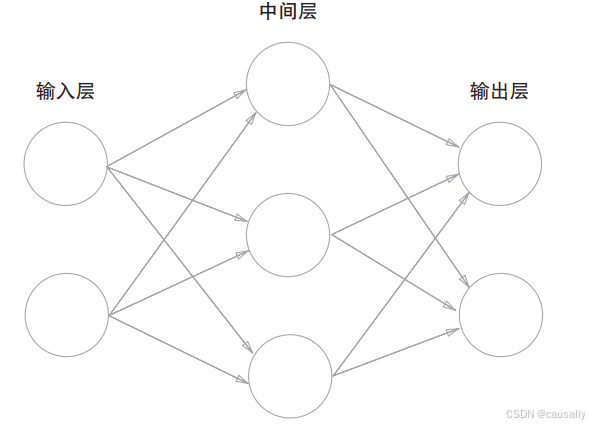
中间层便是由三个感知机组成，将输入层传递的输入信号做处理后会输出信号，作为下一层的输入信号，不太理解的人可以想象一下神经元之间是如何传递。而感知机不会单纯计算 $eq?y%3D%5Comega%201%20x1+%5Comega%202%20x2%20+b$ ，它会将y值进行函数处理。就好像前面公式得到x值，然后利用f（x）得出输出值。所以请记住，是先计算加权总和，再用函数转换。而函数在神经网络中被称为激活函数。

接下来，热烈欢迎激活函数的登场。

因为神经网络中会大量使用矩阵，所以定义函数时x默认为数组。

2.3 激活函数

激活函数是用来把输入信号总和转换为输出信号。常见的包括sigmoid函数、阶跃函数（step_function）、ReLU函数、softmax函数以及恒等函数。而为了发挥叠加层的优势。激活函数必须是非线性函数（线性函数是一条笔直的直线）。

回归函数用恒等函数，分类函数用softmax函数，所以在手写数字识别的神经网络中最后一层使用softmax。

2.3.1 sigmoid

公式为 $eq?y%3D%5Cfrac%7B1%7D%7B1+e%5E%7B-x%7D%7D$

import matplotlib.pyplot as plt
import numpy as np
def sigmoid(x):                  #sigmoid函数代码实现
    return 1/(1+np.exp(-x))
x=np.arange(-5.0,5.0,0.1)        #生成-5到5，差值为0.1的数组
y=sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1,1)               #y的取值范围
plt.show()

sigmoid函数的图形

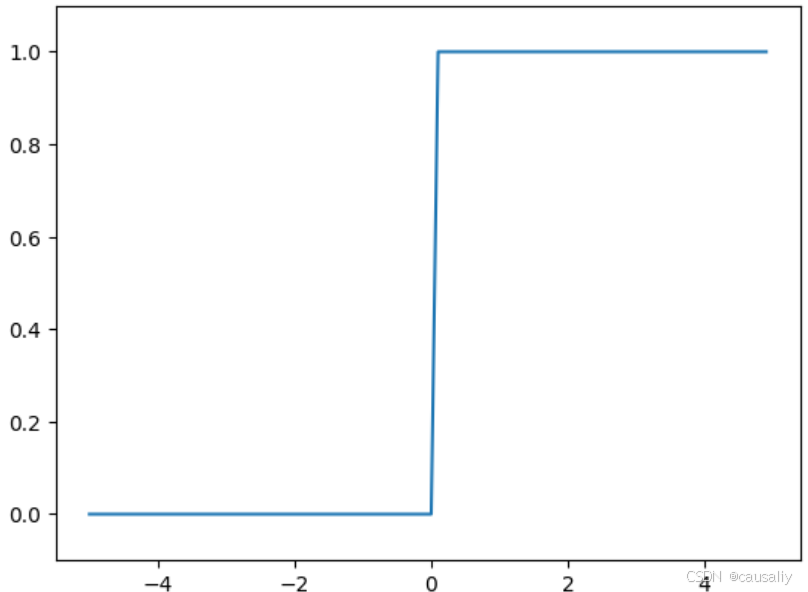
2.3.2 阶跃函数

当输入超过0时，输出1，否则输出0。

import matplotlib.pylab as plt
import numpy as np
#简单版
def step_function(x):
    y=x>0
    return y.astype(np.int32)              #转换为整数，共32位，占4个字节

def step_function(x):                      #考虑到了x为数组
    return np.array(x > 0, dtype=np.int32) #x>0会将x中大于0的数变为True，其它为False
                                           #而dtype=np.int32会改变数值类型，True为1，False为0
x=np.arange(-5.0,5.0,0.1)
y=step_function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)                         #y值范围
plt.show()

2.3.3 ReLU函数

但输入大于0时，原值输出；小于0时，输出0。

import numpy as np
import matplotlib.pylab as plt

def relu(x):
    return np.maximum(0, x)      #选择0和x中的最大值

x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1.0, 5.5)
plt.show()

2.3.4 softmax函数

公式为 $eq?y_%7Bk%7D%3D%5Cfrac%7Be%5E%7Ba_%7Bk%7D%7D%7D%7B%5Csum_%7Bi%3D1%7D%5E%7Bn%7De%5E%7Ba_%7Bi%7D%7D%7D$ ,分母是所有输入信号的指数函数和，分子是 $eq?a_%7Bk%7D$ 的指数函数。

而在计算机处理时，数值必须在4字节到8字节的宽度范围内，即int32到int64，而指数函数存在人们常说的“指数爆炸”问题，所以会有溢出问题，下面是解决方案：

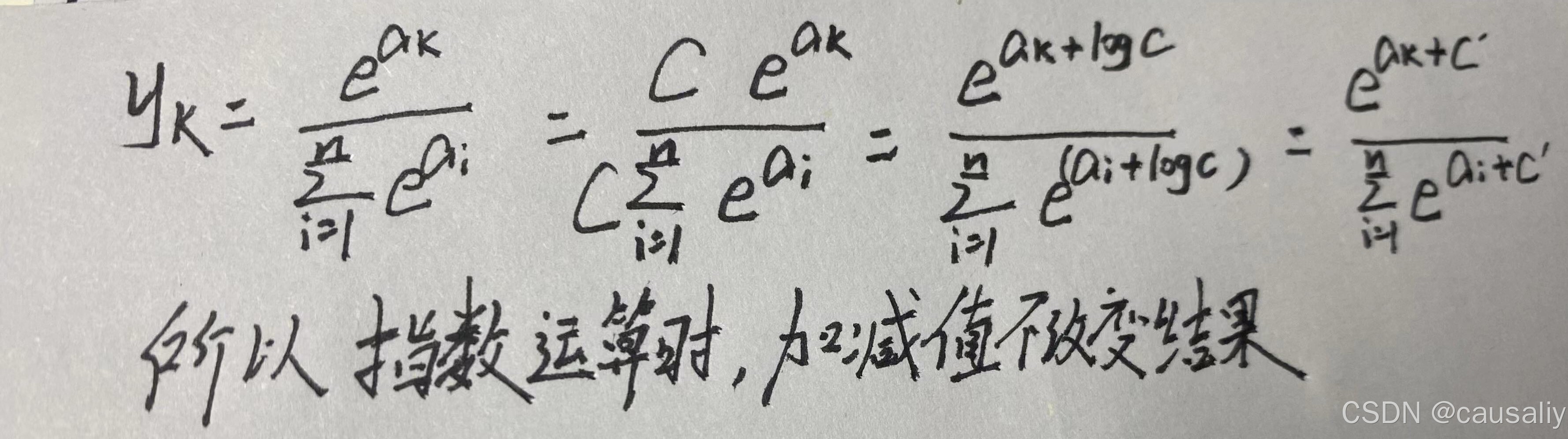
c可以取任意值，但这里一般会使用输入信号中的最大值。

def softmax(x):
    if x.ndim == 2:                                #二维数组说明可以同时输入多个数据，方便进行批处理
        x = x.T                                    #矩阵转置是为了避免下一行代码因为结构不同不能相减
        x = x - np.max(x, axis=0)                  #axis=0是寻找矩阵列中的最大值，axis=1是行中的最大值。
        y = np.exp(x) / np.sum(np.exp(x), axis=0)  #计算每一列的和
        return y.T                    

    x = x - np.max(x) # 溢出对策
    return np.exp(x) / np.sum(np.exp(x))

这里需要注意的是，数组内数据经过指数处理后，不同元素间的大小关系不变。而输出的值总和为1，可以看成“概率” 。而这个函数一般会用在神经网络层中的最后一层，用于寻找“概率”最大值，用来作为预测值。

至于恒等函数，顾名思义，该函数会不做任何处理输出输入信号。

2.4 手写数字识别

不知道大家还有没有记得矩阵相乘时两个矩阵的结构要求，那便是对应维度的元素个数需要相同，比如：

还有矩阵相乘如何得到新矩阵，这些也是需要会的：

2.4.1 各层间信号传递

如果使用矩阵的乘法运算，我们可以用 $eq?A%3DXW+B$ 来计算总和，其中A为总和、X为输入数据、W为权重、B为偏置，而且这些都是数组，所以要注意数组间的结构是否符合要求。所以这一层计算得到的A经过激活函数转换后会作为下一层的B,以此类推。

下面是层与层之间的信号传递图。

下面给出三层神经网络信号传递的代码实现：

def predict(network, x):
   #以数组形式保存不同层的权重和偏置
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
 
    a1 = np.dot(x, W1) + b1       #np.dot 是用来进行矩阵相乘计算的 
    z1 = sigmoid(a1)              #第一层的输出函数
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y

在接下来的识别中，使用的是非常经典的MNIST手写数字图像集，由0到9的数字图像构成，包含6万张28*28像素的图片，并且每张图片还标有正确数字的标签。

我们会使用load_mnist函数读入MNIST数据集，具体代码如下：

def load_mnist(normalize=True, flatten=True, one_hot_label=False):
    """读入MNIST数据集
    
    Parameters
    ----------
    normalize : 将图像的像素值正规化为0.0~1.0
    one_hot_label : 
        one_hot_label为True的情况下，标签作为one-hot数组返回
        one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组
    flatten : 是否将图像展开为一维数组
    
    Returns
    -------
    (训练图像, 训练标签), (测试图像, 测试标签)
    """
    if not os.path.exists(save_file):
        init_mnist()
        
    with open(save_file, 'rb') as f:
        dataset = pickle.load(f)
    
    if normalize:
        for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].astype(np.float32)
            dataset[key] /= 255.0
            
    if one_hot_label:
        dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
        dataset['test_label'] = _change_one_hot_label(dataset['test_label'])
    
    if not flatten:
         for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].reshape(-1, 1, 28, 28)

    return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label'])

使用该函数会输出训练数据的图片、训练数据的标签、测试数据的图片、测试数据的标签。

load_mnist函数的三大参数有不同作用，normalize=True可以将输入的图像进行正规化处理，即将所有单精度数据都同时除以255，使范围控制在0~1.0；

flatten（中文意思为扁平化）会将输入图像的三维数组（1*28*28）数据展开为一维数组，其中1是指输入图片数量，28*28是单个图片的像素规格，所以会保存为有784（28*28）个元素组成的数组；

最后的one_hot_label设置的是参数，若为True则会将单纯一个数字的标签转换为大小为10的数组，除了正确解值对应的下标为1，其它都是0，例如标签2，它的数组为[0,0,1,0,0,0,0,0,0,0]，1对应的下标便是它的正确解。

2.4.2 神经网络的推理处理

该神经网络的输入层有784个神经元（对应784个像素数据），输出层有10个神经元（对应0到9），此外，还有两个隐藏层，第一个隐藏层有50个神经元，第二个隐藏层有100个神经元。

接下来为了流程的正常推进，我们定义get_data、init_network、predict三个函数：

def get_data():   #数据导入，并输出训练数据的图像与对应的标签
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test


def init_network():     #会读取保存在pickle（后缀为pkl）文件内的权重、偏置
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)    #将文件中的数据解析为一个Python对象，即输出字典
    return network


def predict(network, x):   #神经网络各层信号传递的代码
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y

而评价神经网络的推理处理能力，我们使用识别精度评价，可以在多大程度上正确分类：

x, t = get_data()           #x、t分别保存训练数据的图像和标签
network = init_network()    #init_network保存各层的权重和偏置
accuracy_cnt = 0
for i in range(len(x)):
    y = predict(network, x[i])    #y是输入图像数据经过神经网络三层后推理值
    p= np.argmax(y)               #获取概率最高的元素的索引
    if p == t[i]:                 #若推理值与标签相同，则加一
        accuracy_cnt += 1

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))   #识别精度

用predict函数进行分类，用数组形式输出各个标签的概率，然后我们使用np.argmax输出这个数组最大值的下标（0到9的数字与数组下标一一对应，比如2的下标也是2）。最后会显示“Accuracy:0.9352"。下面是具体的代码：

import numpy as np
import funs as f
import matplotlib.pyplot as plt
import time
from mnist import *    #load_minist

(train_img,train_label),(test_img,test_label) = load_mnist()  #调用了mnist.py的load_mnist函数
print(train_label.shape)           #（60000，1）    60000个对应标签
print(train_img.shape)             #（60000，784）  60000张一维1*784的图像数据
print(test_label.shape)            #（10000，1）
print(test_img.shape)              #（10000，784）

# print(train_img[0])
print(train_label[0])  # 5

# plt.imshow(train_img[0].reshape(28,28),camp='Greys_r')
def img_show(img):
     plt.imshow(img,cmap='Greys_r') #将图像数据显示为图形，并对图像进行不同的可视化设置
                    #camp是设置颜色  interpolation定义了图像在放大或缩小时的插值方式
                    # alpha：透明度取值范围为0（完全透明）到1（完全不透明）之间。
                    #vmin和vmax：用于设置显示的数据值范围。
     plt.show()
img = train_img[0].reshape(28,28)  #将数据结构改为28*28的二维数组
img_show(img)

def init_network():  #返回权重和偏置数据
     with open("sample_weight.pkl",'rb') as f:  # 读取.pkl文件
#首先使用open()函数打开.pkl文件，文件模式为’rb’，表示以二进制读取模式打开文件。
 #rb: 以二进制格式打开一个文件用于只读。文件指针将会放在文件的开头  具体参数请看https://blog.csdn.net/weixin_44290661/article/details/103028446
          network = pickle.load(f)  #该方法传入的是文件对象，使用load的方法将数据从pkl文件中读取出来
          return network   #sample_weight.pkl中保存的是各层的权重和偏置

def predict(network,x):  #此神经网咯有一个输入层，两个隐藏层，一个输出层
     W1,W2,W3 = network['W1'],network['W2'],network['W3']
     b1,b2,b3 = network['b1'],network['b2'],network['b3']
# 这些自定义函数在functions.py有说明
     a1 = np.dot(x,W1) + b1  #dot函数是矩阵相乘的作用
     z1 = f.sigmoid(a1)      #利用sigmiod函数计算出第一层的值，并以此作为下一层的初始值
     a2 = np.dot(z1,W2) + b2 #以下过程等同
     z2 = f.sigmoid(a2)
     a3 = np.dot(z2,W3) + b3
     y = f.softmax(a3)    #输出层的激活函数所有加起来等于1，近似于概率
     return y   #输出值为一维数组

network = init_network()  #将权重偏置导入到network
accuracy_cnt = 0
strat_time=time.time()
for i in range(len(test_img)):
     y = predict(network,test_img[i])  #test_img[i]输出的是1*784数组，索引共60000
     print("实际值为:",test_label[i],"预测为:",np.argmax(y))
     #numpy.argmax(array, axis) 用于返回一个numpy数组中最大值的  索引值  。当一组中同时出现几个最大值时，返回第一个最大值的索引值。
     p = np.argmax(y)  #取输出层10个数中最大值为预测值，即取得是概率最大值
     if p == test_label[i]:  #test_label[i]中存放的是实际值
         accuracy_cnt += 1
end_time=time.time()
print("Accuracy:" + str(float(accuracy_cnt) / len(test_img)))
print("运行时间："+str(end_time-strat_time))

而具体的输出情况为：

最后，我们提及一下正规化(normalization)，比如load_mnist中的normalize参数，将图像的各个像素除以255，是得数据得值在0~1.0范围内。像这种对输入数据进行某种既定得转换称为预处理（pre-processing）。预处理在神经网络中非常使用，可以有效提高识别性能和学习的效率

2.4.3 输入图像的批处理

能够一次性处理多个图片便是批处理，与单独一次一次处理图片不同，批处理可以大幅度缩短每张图片的处理时间，因为它减少了数据读入时间。所以，批处理计算大型数组比分开计算的速度更快。

而由于数组相乘的结构特点，我们可以在最前面改变数据数量，例如下面最前面的100，而100便是一批。

所以最后输出结果为[100,10],这个数组意思便是有100个大小为10（0~9对应的概率）结果。

batch_size=100  #设置批处理中批的大小，可以换其他值
(train_img,train_label),(test_img,test_label) = load_mnist()#调用了mnist.py的load_mnist函数
#(训练图像, 训练标签),      (测试图像, 测试标签)
network=init_network()
accuracy_cnt=0
start_time=time.time()
for i in range(0,len(test_img),batch_size):
     x_batch=test_img[i:i+batch_size]  #同理，输出100个1*784的一维数组构成的二维数组
     y_batch=predict(network,x_batch)  #输出100*10对应的输出值一维数组
     p=np.argmax(y_batch,axis=1)       #在指定沿着第一维方向找到最大值，即输出每一维度的最大值（每一个输出层的最大值）索引
     accuracy_cnt += np.sum(p == test_label[i:i + batch_size])  #相同结构数组比较，返回True或False布尔型，并计算True的数量
end_time = time.time()
print("Accuracy:" + str(float(accuracy_cnt) / len(test_img)))
print("运行时间:" + str(end_time - start_time))

#以上两种处理方法运算时间不同是因为下面一种运用了静态数据批处理方法，减少了数据读入时间，将更多时间用于计算上，可以缩短时间

这里便是通过批处理处理数据，批大小为100，以100为步距进行遍历数据。

p=np.argmax(y_batch,axis=1) 会寻找矩阵中每一行的最大值下标，而一行便是一个图片运行结果。

而accuracy_cnt += np.sum(p == test_label[i:i + batch_size])代码会将输出结果与测试标签相比，相同的为Ture，不同的为False，最后的np.sum会求True的数量。

下面的运行时间是进行批处理过的，我们可以看出批处理的确可以大幅度减少运行时间。

第3章神经网络的学习

在这一章里，有运用到数分的偏导以及梯度，忘记的只需要去记一下偏导的定义以及推导。而本章目的是了解神经网络是如何自动寻找最优参数的原理及其实现。

3.1 从数据中学习

在庞大的神经网络层中，可能含有上千万的权重偏置参数，如何都是通过人为干预输入的话会是非常恐怖的事，而神经网络便是可以通过自己的学习，利用数据找到最优参数。

在识别图像的时候，我们人眼识别可以非常轻松知道这是什么数字，但如果让你说出是如何识别的，你或许可以回答通过观察这个数字的特征。而神经网络也可以如此，先从图片中提取特征量，再用机器学习学习这些特征量模式，并通过特征量从输入数据中提取重要数据，而对于不同的问题，也必须使用相适应的特征量（专门设计），但可惜的是，这些特征量的设计依旧是人工参与。

在接下来的内容中，将数据分为训练数据和测试数据。训练数据是用来投喂神经网络进行学习，而测试数据可以说是来评估学习情况的，避免只会训练数据而其它的不会，这是模型的“泛化能力”，能够对那种未学习过的数据进行处理。

另外，能够处理该数据集却无法处理其它数据集，这种现象被称为过拟合，在后面会提到避免过拟合的措施。

3.2 损失函数

下面的内容可以提上小板凳认真听讲了，我们通过损失函数的值来评估学习结果，损失函数值越小，与监督数据（训练数据）误差越小。

而用作损失函数的函数中最有名的便是均方误差和交叉熵误差。

3.2.1 均方误差

均方误差公式为 $eq?E%3D%5Cfrac%7B1%7D%7B2%7D%5Csum_%7Bk%7D%5E%7B%7D%28y_%7Bk%7D-t_%7Bk%7D%29%5E%7B2%7D$ ， $eq?t_%7Bk%7D$ 为监督数据， $eq?y_%7Bk%7D$ 为输出数据，k为数据维度。

均方误差会计算输出数据与正确解监督数据的对应元素差的平方，然后求和。输出结果与监督数据标签都是大小为10的数组，而标签是因为load_mnist的one-hot为True。

def mean_squared_error(y, t):
    return 0.5 * np.sum((y-t)**2)
#y和t的数组结构相同，对应位置的数据相减并平方

3.2.2 交叉熵误差

交叉熵误差公式为 $eq?E%3D-%5Csum_%7Bk%7D%5E%7B%7Dt_%7Bk%7Dlogy_%7Bk%7D$ ，因为 $eq?t_%7Bk%7D$ 中除了正确解下标处的值为1，其余9个都是0，所以交叉熵误差的值是由正确解标签所对应的输出结果决定，所以 $eq?E%3D-logy_%7Bk%7D$ 。而对数图像长什么样我就不展示了。

在log函数中，趋近于0的y值会趋近于负无穷，所以为了避免这种可能，我们会采取保护性措施，以防止无限大发生。

def cross_entropy_error(y,t):
     delta=1e-7
     return -np.sum(t*np.log(y+delta))

3.2.3 mini-batch学习

在学习过程中，找到损失函数值尽可能小对应的参数值。在计算损失函数值需要同时对所有训练数据进行处理，把所有输入函数对应的损失函数进行求和。

对应的交叉熵误差改为 $eq?E%3D-%5Cfrac%7B1%7D%7BN%7D%5Csum_%7Bn%7D%5E%7B%7D%5Csum_%7Bk%7D%5E%7B%7Dt_%7Bnk%7Dlogy_%7Bnk%7D$ ， $eq?t_%7Bnk%7D$ 和 $eq?y_%7Bnk%7D$ 表示第n个数据（0~训练数据数-1）的第k个元素（0~9）。最后除以N训练数据数量进行正规化，也就是求单个数据的平均损失函数。而且在MNIST数据集里，含有60000个训练数据，如果以这六万份数据作为对象，就会花费很长时间，不太现实。所以我们从全部数据中选出一部分作为小批次，也就是mini-batch。比如从60000里面选100份，以这100份数据进行学习。利用一部分样本来近似计算整体，跟统计得随机抽样一样。

import sys,os
sys.path.append(os.pardir)     #可以导入文件夹里父目录下如何文件，而不局限于当前目录
import numpy as np
from dataest.mnist import load_mnist
(x_train,t_train),(x_test,t_test) =\
 load_mnist(normalize=True,one_hot_label=True)

print(x_train.shape)    #(60000,784)
print(t_train.shape)    #(60000,10)

训练数据x_train的结构是（60000，784）说明有60000张包含784个数据的数组。不过这里需要提的是shape的用法：

t_train.shape     #(60000,784)  读取矩阵的大小
t_train.shape(0)  #60000   读取第一维度的长度，这里便是行数
t_train.shape(1)  #784    列数

接下来就是运用mini-batch来寻找小批次数据，比如说100，这里需要100个数都是随机的，下面是实现代码：

train_size=x_train.shape(0)  #60000
batch_size=100
batch_mask=np.random.chioce(train_size,batch_size)  
 #生成从0到train_size随机抽取batch_size个整数数据，即作为索引
x_batch=x_train[batch_mask]   #利用索引寻找相对应得数据和标签
t_batch=t_train[batch_mask]

3.2.4 交叉熵误差mini-batch

相比较之前可以处理单个数据的cross_entropy_error（交叉熵误差公式代码实现）函数，这里就需要可以处理批量数据得代码：

def cross_entropy_error(y, t):
    if y.ndim == 1:                #如果处理单个数据的话，需要将t、y变为一维
        t = t.reshape(1, t.size)   #监督数据
        y = y.reshape(1, y.size)   #神经网络输出
             
    if t.size == y.size:           #这个是为了将one-hot=True的标签转化为只含正确解值的数组
        t = t.argmax(axis=1)       #寻找最大值对应的下标，比如[0,0,1,0,0,0,0,0,0,0]会被转化为正 
                                   #确解为2

    batch_size = y.shape[0]   #batch_size为数据数量
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
 #np.arange(batch_size)会生成[0,1,2,3.....batch_size-1]的数组
 #y[np.arange(batch_size), t]因为t是这些批量数据对应的正确解，所以这个代码会实现抽出正确解标签对
 #应的神经网络输出，可能很不好理解
 #比如np.arange(batch_size)生成[0,1,2,3,4],而正确解t是[2,7,0,9,4]。最后会生成如[0,2],[1,7],
 #[2,0]等形式，代表第1个数据下标为2的元素值，第2个数据下标为7的元素值，第3个数据下标为0的数据值

为什么要这么实现呢？因为交叉熵的值只与正确解对应的输出值有关。

完成了交叉熵误差的代码实现后，而交叉熵误差用作损失函数值。在神经网络的学习中，寻找最优参数（权重和偏置）时，要寻找损失函数尽可能小所对应的参数。

而下面内容便是与偏导有关。因为在复杂神经网络中，会拥有大量的参数，不同的参数对于损失函数的影响也不同，就很像数分里面的多元函数，最简单的例子就时 $eq?z%3Df%28x%2Cy%29$ ,我们在探求x或者y对于z的影响时，会利用偏导求出在其他因素不变的情况下，随一种因素变化的变化率，就如 $eq?%5Cfrac%7B%5Cpartial%20z%20%7D%7B%5Cpartial%20x%7D$ 和 $eq?%5Cfrac%7B%5Cpartial%20z%20%7D%7B%5Cpartial%20y%7D$ 。

3.3 偏导与梯度

在讲偏导的内容前，我们先回顾下一个函数的导数是怎么计算的：

$eq?%5Cfrac%7Bdf%28x%29%29%7D%7Bdx%7D%3D%5Clim_%7B%7D%5Cfrac%7Bf%28x+h%29-f%28x%29%7D%7Bh%7D$

不过因为f（x+h）-f（h）是趋近于f（x+0.5h）的导数，所以我们将函数改为：

$eq?%5Cfrac%7Bdf%28x%29%29%7D%7Bdx%7D%3D%5Clim_%7B%7D%5Cfrac%7Bf%28x+h%29-f%28x-h%29%7D%7B2h%7D$

这叫做中心差分。

h虽然是趋近于0的，但还是需要为其赋一个小值，而由于计算机会省略精细部分的数值，比如小数点8位以后的数值是不会保留的。而太大也不行，所以最终选择1e-4 ：

def numerical_diff(f, x):
    h = 1e-4 # 0.0001
    return (f(x+h) - f(x-h)) / (2*h)

我们列举一个例子，设函数为 $eq?y%3D0.01x%5E%7B2%7D+0.1x$ ，对其求导数也很好做，下面是函数图像以及对应的x=5处的切线：

import numpy as np
import matplotlib.pylab as plt
def numerical_diff(f, x):
    h = 1e-4 # 0.0001
    return (f(x+h) - f(x-h)) / (2*h)
def function_1(x):
    return 0.01*x*x+0.1*x
x=np.arange(0.0,20.0,0.1)
y1=function_1(x)
y2=numerical_diff(function_1,5)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x,y1)
plt.plot(x,y2*(x-5)+function_1(5))    #切线求法：y=k（x-x0）+y0
plt.show

下面是代码运行结果：

3.3.1 偏导数

我们设函数为 $eq?f%28x_%7B0%7D%2Cx_%7B1%7D%29%3Dx_%7B0%7D%5E%7B2%7D+x_%7B1%7D%5E%7B2%7D$ ，函数代码是：

def  function_2(x):
     return x[0]**2+x[1]**2
     #用return np.sum(x**2)也可以

在多元函数的一阶泰勒公式中，我们学习了一维梯度和二维黑塞矩阵。而在计算多元函数的极值时，其必要条件是 $eq?%28%5Cfrac%7B%5Cpartial%20f%7D%7B%5Cpartial%20x_%7B0%7D%7D%2C%5Cfrac%7B%5Cpartial%20f%7D%7B%5Cpartial%20x_%7B1%7D%7D%29_%7Bx_%7B0%7D%7D%3D0$ ，而在其它地方时，梯度的值是指向最大值的方向。下面是梯度的代码实现：

def _numerical_gradient(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)           #生成与x相同结构，但全为0的数组
    for idx in range(x.size):
        tmp_val = x[idx] 
        x[idx] = float(tmp_val) + h  #计算f（x+h）
        fxh1 = f(x)          
        
        x[idx] = tmp_val - h 
        fxh2 = f(x)                  # 就算f(x-h)
        
        grad[idx] = (fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val             # 还原值
        
    return grad

然后，我们尝试计算一下梯度，下面我们计算一下在（3，4）处的梯度，结果会是（6，8）：

numerical_gradient(function_2,np.array([3.0,4.0]))
#不过要注意的是，3和4要求是小数

然后我们直观观察梯度指向最大值的作用，我们可以确定的是 $eq?f%28x_%7B0%7D%2Cx_%7B1%7D%29%3Dx_%7B0%7D%5E%7B2%7D+x_%7B1%7D%5E%7B2%7D$ 函数最小在（0，0），所以图上所有箭头都是指向（0，0）。而要指向最小值方向就可以加个-，指向反方向。

if __name__ == '__main__':
    x0 = np.arange(-2, 2.5, 0.25)
    x1 = np.arange(-2, 2.5, 0.25)
    X, Y = np.meshgrid(x0, x1)          # 可以生成更高维度的坐标矩阵，这里就可以使XY升为二维
    
    X = X.flatten()     #多维数据的降维函数,例如x是2*3*4的三维，降维后变成大小（2*3*4=24）的一维数组
    Y = Y.flatten()
    
    grad = numerical_gradient(function_2, np.array([X, Y]) )
    
    plt.figure()   #是一个用于创建新的图形窗口的函数，它可以帮助我们设置图形窗口的大小、分辨率和其他属性
    plt.quiver(X, Y, -grad[0], -grad[1],angles="xy",color="#666666")   #X、Y确定位置，grad确定箭头方向，angle确定确定箭头角度
    plt.xlim([-2, 2])  #x范围
    plt.ylim([-2, 2])
    plt.xlabel('x0')
    plt.ylabel('x1')
    plt.grid()      #添加网格线
    plt.legend()
    plt.draw()      #重新绘制图形
    plt.show()      #显示图形

运行结果如下：

而且我们发现，离最小点远的，箭头长度更长。而利用梯度来寻找函数最小值，不过在复杂函数中，梯度指示方向都不是函数值最小值，就像你站在一个盆地里，你知道这是你在附近可以找到最低的地方，但你不能确定这是地球上最低的地方。在梯度法中，我们从当前地方沿着梯度方向前进一定距离，然后在新地方重新求梯度，再沿着新梯度方向前进，以此反复，不断前进。

用公式表示梯度法，如下：

$eq?x_%7B0%7D%3Dx_%7B0%7D-%5Ceta%20%5Cfrac%7B%5Cpartial%20f%7D%7B%5Cpartial%20x_%7B0%7D%7D$

$eq?x_%7B1%7D%3Dx_%7B1%7D-%5Ceta%20%5Cfrac%7B%5Cpartial%20f%7D%7B%5Cpartial%20x_%7B1%7D%7D$

其中， $eq?%5Ceta$ 是学习率，其大小影响你沿梯度方向前进距离，一般而言，过大过小都不可取。沿梯度方向是减去梯度。而在神经网络的学习中，一般会一边改变学习率的值，一遍确定是否正确学习，这后面会讲到。

def gradient_descent(f, init_x, lr=0.01, step_num=100):
    x = init_x  #数组，初始值也就是当前位置

    for i in range(step_num):  #更新次数

        grad = numerical_gradient(f, x)  #求梯度
        x -= lr * grad  #沿梯度方向

    return x

现在我们利用梯度法求 $eq?f%28x_%7B0%7D%2Cx_%7B1%7D%29%3Dx_%7B0%7D%5E%7B2%7D+x_%7B1%7D%5E%7B2%7D$ 的最小值：

init_x=np.array([-3.0,4.0])
gradient_descent(function_2,init_x=init_x,lr=0.1,step_num=100)
#array([-6.11110793e-10,8.14814391e-10])

基本以及非常接近（0，0），而随着更新次数的增加，距离最小值更近，梯度更小，更新值也会越来越小。而像学习率这种属于超参数，与权重偏置的性质不同。

3.3.2 神经网络的梯度

梯度是指损失函数关于权重参数的梯度，权重形状2*3的梯度如下

我们定义simpleNet函数来实现梯度：

import sys, os
sys.path.append(os.pardir)  #为了导入父目录中的文件而进行的设定
import numpy as np
from common.functions import softmax, cross_entropy_error
from common.gradient import numerical_gradient


class simpleNet:
    def __init__(self):
        self.W = np.random.randn(2,3)  #在[0,1)范围内生成给定维度数组

    def predict(self, x):
        return np.dot(x, self.W)         #矩阵相乘

    def loss(self, x, t):
        z = self.predict(x)
        y = softmax(z)                   #经过激活函数
        loss = cross_entropy_error(y, t) #计算交叉熵误差

        return loss

x = np.array([0.6, 0.9])
t = np.array([0, 0, 1])

net = simpleNet()

f = lambda w: net.loss(x, t)         #等价于def f(w):
	                                 #         return net.loss(x, t)

dW = numerical_gradient(f, net.W)

print(dW)

3.3.3 学习算法的实现

梯度下降法的步骤为：1、抽取mini-batch，2、计算梯度，3、更新梯度，4、重复123。

而随机梯度下降法有SGD函数实现。

3.3.4 2层神经网络的类

下面将2层神经网络实现为TwoLayerNet的类，实现过程如下：

import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
from common.functions import *
from common.gradient import numerical_gradient

class TwoLayerNet:

    def __init__(self, input_size, hidden_size,   output_size,     weight_init_std=0.01):
        # 初始化权重      输入层     中间隐藏层   输出层的神经元数量        正规化    
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
                                             #返回一个或一组样本，具有标准正态分布
        self.params['b1'] = np.zeros(hidden_size)   #生成给定形状和类型的用0填充的数组
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
    
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)   #最后的损失函数是用softmax，用来求概率最大值
        
        return y
        
    # x:输入数据, t:监督数据
    def loss(self, x, t):
        y = self.predict(x)
        return cross_entropy_error(y, t)   #交叉熵误差的损失函数
    
    def accuracy(self, x, t):      #预测精确值
        y = self.predict(x)
        y = np.argmax(y, axis=1)   #寻找每一行的最大值索引
        t = np.argmax(t, axis=1)
        
        accuracy = np.sum(y == t) / float(x.shape[0])  #求数组中为True的数量和，并求精确值
        return accuracy
        
    # x:输入数据, t:监督数据
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)
        
        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])  #求对应参数的梯度
#计算关于损失函数在w1参数处的梯度，各层参数都需要
        grads['b1'] = numerical_gradient(loss_W, self.params['b1']) 
#寻找损失函数最小处对应的参数值
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
        
        return grads  #返回不同层的权重偏置参数对应的梯度值

3.3.5 epoch

在前面我们可以计算出mini-batch的识别精度，但是在神经网络中我们需要确定能够识别训练数据以外的数据，否则便会发生过拟合，即不能正确识别训练数据外的数字图像。一般会定期对训练数据和测试数据记录识别精度，每经过一个epoch，便记录一次。epoch是指mini-batch都被用过时，就称为一个epoch。比如60000数据，mini-batch为100，那epoch就是60。

import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from mnist import load_mnist
from two_layer_net import TwoLayerNet

# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

iters_num = 10000               # 适当设定循环的次数
train_size = x_train.shape[0]   #训练数据的数量
batch_size = 100
learning_rate = 0.1

train_loss_list = []  #记录损失函数值，记录一次便更新一次参数值，通过损失函数变化区间可以查看学习情况
train_acc_list = []   #记录训练数据的识别精度
test_acc_list = []    #记录测试数据的识别精度

iter_per_epoch = max(train_size / batch_size, 1)  #平均每个epoch的重复次数

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
                                #在（0，train_size)范围内选batch_size个数据
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    # 计算梯度
    grad = network.numerical_gradient(x_batch, t_batch) #计算在损失函数公式中在参数位置对应
#的梯度
    #grad = network.gradient(x_batch, t_batch)
    
    # 更新参数
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
    
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
    if i % iter_per_epoch == 0:    #每过一个epoch，便记录一次训练和测试数据的识别精度
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))

观察在不同epoch里训练和测试数据对应的识别精度，若是识别精度大致相同可以说明未发生过拟合现象。

第4章误差方向传播法

在看本章内容前，可以提前观看书本相对应内容，看完后再结合观看。

什么是误差方向传播法，其实就是一种可以高效计算权重偏置参数的梯度方法。与反向相反的便是正向传播，从出发点到结束点的传播。而正向传播流程里不仅有加减乘除，还有其它大量的的计算符号，这导致方向传播也有相对应数量的计算公式。不过这里讲的大多是加减乘除基础内容。

在该正向流程图里面，每一个圆（节点）里面都是一个计算符号，各个节点的计算都是局部计算，它可以将复杂的计算分为众多简单的局部计算，而且也可以使用方向传播计算导数。

4.1 链式法则

正向传播：将计算结果正向传递。

方向传播：乘以局部导数方向传播。

例如正向传播是 $eq?y%3Dx%5E%7B2%7D$ 函数，所以方向传播就会乘以导数 $eq?2x$ 。而链式法则便是可以通过层层传递局部导数，很像学过的复合函数，举简单例子便是 $eq?z%3Dln%25uFF08x+1%29$ 是由 $eq?z%3Dln%20y$ 和 $eq?y%3Dx+1$

两函数构成。

4.2 方向传播

这一小节内容可以概况成两小句内容：

加法节点：上游值不变地传到下游（结束点是上游）

乘法节点：将上游值乘以正向传播值得“翻转值”（也就是乘以另一路的值），例如：

正向传播时上路是5，下路是10，所以求上路反向传播时会乘以“翻转值”5，而求下路的便会乘以10。

4.3 MulLayer和Addlayer

定义乘法层MulLayer和加法层Addlayer函数类，其中forward是正向传播，backward是方向传播。

class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None

    def forward(self, x, y):  正向传播时自然是两数相乘并传递
        self.x = x
        self.y = y                
        out = x * y

        return out

    def backward(self, dout):   方向传播时需要翻转值，所以x乘以y，y乘以x
        dx = dout * self.y
        dy = dout * self.x

        return dx, dy

class AddLayer:
    def __init__(self):
        pass

    def forward(self, x, y):
        out = x + y

        return out

    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1

        return dx, dy

接下来我们举苹果的例子：

当我们探究苹果的个数对于苹果价钱的影响程度时，可以就可以通过反向传播来计算苹果的个数对于价钱的导数。

from layer_naive import *

apple = 100    #苹果单价
apple_num = 2  #苹果数量
tax = 1.1      #税收

mul_apple_layer = MulLayer()  #第一个节点
mul_tax_layer = MulLayer()    #第二个节点
 
# forward   正向传播
apple_price = mul_apple_layer.forward(apple, apple_num)
price = mul_tax_layer.forward(apple_price, tax)

# backward  方向传播
dprice = 1
dapple_price, dtax = mul_tax_layer.backward(dprice)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)

print("price:", int(price))              #正向传播的结束点值  220
print("dApple:", dapple)                 #方向传播第一节点上路值  1.1
print("dApple_num:", int(dapple_num))    #110
print("dTax:", dtax)                     #方向传播第一节点下路值  200

第二个例子：同时买苹果和橘子的例子

from layer_naive import *
#经过正向传播后，四个不同节点的layer会保存对应的输入，方向传播时乘以翻转便可
apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1

# layer      几个局部便有几个变量
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()

# forward    按计算的正向流程走便可以
apple_price = mul_apple_layer.forward(apple, apple_num)  # (1)
orange_price = mul_orange_layer.forward(orange, orange_num)  # (2)
all_price = add_apple_orange_layer.forward(apple_price, orange_price)  # (3)
price = mul_tax_layer.forward(all_price, tax)  # (4)

# backward   依次按方向流程来，一分为二
dprice = 1   #相同节点处用相同的layer
dall_price, dtax = mul_tax_layer.backward(dprice)  # (4)
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price)  # (3)
dorange, dorange_num = mul_orange_layer.backward(dorange_price)  # (2)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)  # (1)

print("price:", int(price))
print("dApple:", dapple)
print("dApple_num:", int(dapple_num))
print("dOrange:", dorange)
print("dOrange_num:", int(dorange_num))
print("dTax:", dtax)

4.4 激活函数层

我们可以将计算图思路用到神经网络，可以将用激活函数来替代节点，将神经网络的层实现为一个类。常见的有ReLU层、sigmoid层、Affine/Softmax层。

4.4.1 ReLU层

该激活函数会将对于0的数原值输出，小于0的输出0。正向传播的输入值大于0时，方向传播会原封不动传给下游；如果正向传播的输入值小于等于0时，方向传播传给下游的信号会停在此处。

class Relu:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)   #将x中<=0的数变为True，>0变为False，[1,2,-3]变[F,F,T]
        out = x.copy()         #数组数列的浅复制
        out[self.mask] = 0     #会将False的元素变为0 ,[1,2,0],跟函数作用相同

        return out

    def backward(self, dout):
        dout[self.mask] = 0    #方向传播中会使用正向传播时保存的mask，将上游传来的dout的mask 
                               #中的元素为True的地方设为0，因为True对应负值
        dx = dout

        return dx

4.4.2 Sigmoid层

$eq?y%3D%5Cfrac%7B1%7D%7B1+e%5E%7B-x%7D%7D$ ，根据函数所示：出现了“exp”和“/”的节点。“/”节点正向传递会取导数，方向传递乘以 $eq?-y%5E%7B2%7D$ ，证明过程忽略；“exp”节点正向传播会进行 $eq?y%3Dexp%28x%29$ 处理，方向传播会乘以 $eq?exp%28-x%29$ ，-x也就是正向传播时对应的输出，所以方向传播时需要保存。

方向传播的结果可以有以下化解：

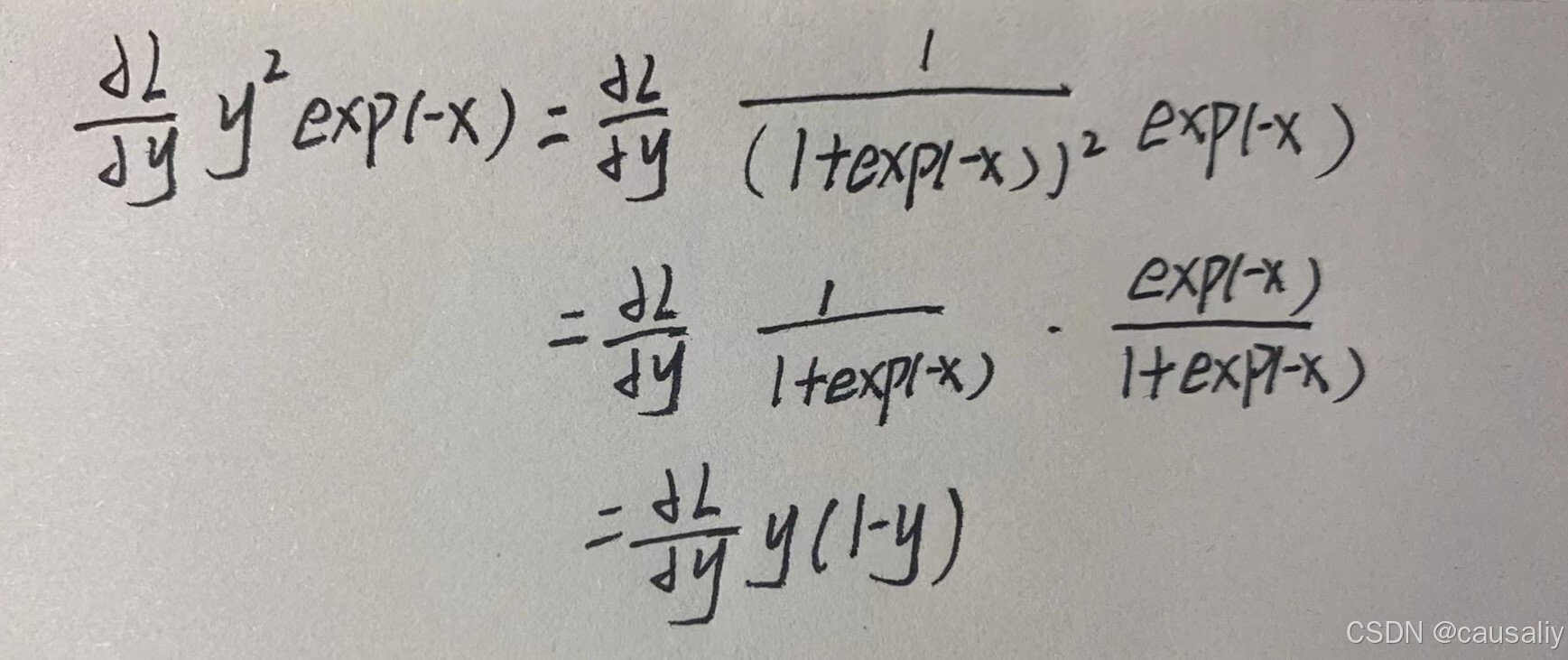
class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = sigmoid(x)
        self.out = out  #正向传播时将值保存在out中
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out
                      #（1-y）y
        return dx

4.4.3 Affine层

在神经网络的正向传播时，我们利用np.dot来进行矩形计算，矩形相乘需要使对应维度的元素个数相同 $eq?Y%3Dnp.bot%28X%2CW%29+B$

在推导反向传播时，第一路的导数和第二路的导数推导如图所示，这里乘以的是翻转值得转置，通过对应维度个数相同可以推导。

class Affine:
    def __init__(self, W, b):
        self.W =W
        self.b = b
        
        self.x = None
        self.original_x_shape = None
        # 权重和偏置参数的导数
        self.dW = None
        self.db = None

    def forward(self, x):
        # 对应张量
        self.original_x_shape = x.shape
        x = x.reshape(x.shape[0], -1)
        self.x = x

        out = np.dot(self.x, self.W) + self.b

        return out

    def backward(self, dout):
        dx = np.dot(dout, self.W.T)        #x路的偏导
        self.dW = np.dot(self.x.T, dout)   #w路的偏导
        self.db = np.sum(dout, axis=0)     #b路的偏导
        
        dx = dx.reshape(*self.original_x_shape)  # 还原输入数据的形状（对应张量）
        return dx

4.4.4 Softmax-with-Loss层

Softmax层会将输入值正规化后输出概率值。在神经网络中有推理和学习两阶段，而在推理阶段时比如手写数字识别里，最后一层就要使用Softmax层，不过Softmax并不改变值大小关系，所以可以不使用Softmax层，而不使用的输出值叫做”得分“。

而Softmax-with-Loss层便可以计算出最后的输出值的同时将损失函数计算出来，下面是Softmax-with-Loss层的方向传播

发现方向传播得到了 $eq?%28y_%7B1%7D-t_%7B1%7D%2Cy_%7B2%7D-t_%7B2%7D%2Cy_%7B3%7D-t_%7B3%7D%29$ 的结果，这是Softmax输出值与监督数据标签相减结果，这是误差的意思，值越小说明误差越小。

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None # softmax的输出
        self.t = None # 监督数据

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        
        return self.loss

    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size  #输出值与标签的误差，除以批大小，便是单个数据的误差
        
        return dx

4.5 章末小节

本章内容多是神经网络学习阶段内容，学习的步骤是先从训练数据中抽取mini-batch，计算损失函数以及各个权重参数的梯度，然后便是进行更新，然后重复步骤。

下面我们对误差方向传播进行代码实现，类TwoLayerNet：

import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict


class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
        # 初始化权重 输入层神经元数量    隐藏层        输出层         规模
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)  #np.random.randn符合高斯分布，生成[0,1),指定规格的数组
        self.params['b1'] = np.zeros(hidden_size)                                       #生成指定形状大小、全是0的数组
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) 
        self.params['b2'] = np.zeros(output_size)

        # 生成层    与神经网络层结构相同
        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])   #第一层的信号计算
        self.layers['Relu1'] = Relu()                                           #经过权重计算后，再经激活函数处理传到下一层
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])

        self.lastLayer = SoftmaxWithLoss()                                      #经过Softmax层算出概率后，计算相对应的损失函数
        
    def predict(self, x):   #导入输入值后，会一条龙服务输出到最后一层Affine的值
        for layer in self.layers.values():    #返回字典中的值
            x = layer.forward(x)              
        
        return x
        
    # x:输入数据, t:监督数据
    def loss(self, x, t):
        y = self.predict(x)   
        return self.lastLayer.forward(y, t)  #求出对应的损失函数
    
    def accuracy(self, x, t):   #求预测的精确度
        y = self.predict(x)     
        y = np.argmax(y, axis=1)  #求出批数据里面每一个“得分”里面最大值下标，不经过Softmax求最大值也可以
        if t.ndim != 1 : t = np.argmax(t, axis=1)  #如果是批处理，标签会从one-hot=True转为求正确解的值，
        
        accuracy = np.sum(y == t) / float(x.shape[0])  #求True的数量，并除以总数便是精确值
        return accuracy
        
    # x:输入数据, t:监督数据
    def numerical_gradient(self, x, t):    #定义法求梯度
        loss_W = lambda W: self.loss(x, t)
        
        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])   #求在损失函数公式里，权重偏置参数的梯度
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
        
        return grads
        
    def gradient(self, x, t):            #方向传播求梯度
        # forward
        self.loss(x, t)  #神经网络输出值与标签正确解的损失函数

        # backward
        dout = 1
        dout = self.lastLayer.backward(dout)  
        
        layers = list(self.layers.values())  #reverse反转函数对列表有用，字典等其它数据类型无效，所以需要用values提取字典的值
        layers.reverse()     #无论是在层里面需要反向传播，在整个神经网络层里面也需要从后向前一个一个经过层，所以需要对列表进行反转
        for layer in layers:
            dout = layer.backward(dout)

        # 设定
        grads = {}
        grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db  #对应层权重偏置参数的梯度
        grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

        return grads

这是一个三层的神经网络，若是想实现多层的神经网络，可以通过类似搭积木方式进行添加。

数值微分有实现简单不易出错等优点，而反向传播实现复杂易出错，所以就需要通过求数值微分的梯度结果来验证反向传播求出的结果，这叫做梯度确认。具体代码不再呈现，其输出是求取数值微分与反向传播之差的误差，并求取其平均值，如果值很小便可说明梯度求取正确

第5章参数优化

本章介绍的是权重参数最优化、初始值。的方法。在前面我们通过梯度求取最优参数方法叫做随机梯度下降法（SGD）。

5.1 SGD、Momentum、AdaGrad和Adam

SGD对于某些形状的函数有很低的效率，比如延申类，这是由于梯度指向小值反向但不指向最小值方向，所以就产生出Momentum、AdaGrad和Adam方法来取代SGD。

5.1.1 Momentum

该方法的解释可以用物理来解释

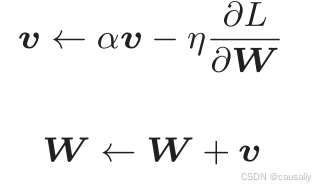
其中的 $eq?%5Calpha%20v$ 相当于阻力（比如摩擦力）， $eq?%5Ceta%20%5Cfrac%7B%5Cpartial%20L%7D%7B%5Cpartial%20W%7D$ 便相当于外力，求出来的 $eq?v$ 便是小球所受合力。而该小球便会向合力方向（或者说是加速度）运动，合力公式本来是 $eq?v%3D%5Ceta%20%5Cfrac%7B%5Cpartial%20L%7D%7B%5Cpartial%20W%7D-%5Calpha%20v$ ，跟前面梯度下降法相同指向方法需要取负值。

class Momentum:

    """Momentum SGD"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr  #   n值          a值
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:     #初始化时v中什么都不保存
            self.v = {}
            for key, val in params.items():        #第一次运行后会生成与参数结构相同的数据                      
                self.v[key] = np.zeros_like(val)
                
        for key in params.keys():   #参数更新
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]   #公式代码实现
            params[key] += self.v[key]

5.1.2 AdaGrad

学习率衰减：随着学习的进行，学习率（lr）会逐渐减少（先大步靠近，再小步接近）

AdaGrad会为每个参数都适应性调整学习率，而不是全体参数一起调整。

$eq?w$ 为权重参数， $eq?%5Cfrac%7B%5Cpartial%20L%7D%7B%5Cpartial%20W%7D$ 表示损失函数关于 $eq?w$ 的梯度， $eq?%5Ceta$ 为学习率。第一个式子保存了以前参数梯度的平方和，通过乘以 $eq?%5Cfrac%7B1%7D%7B%5Csqrt%7Bh%7D%7D$ 来达到调整学习率，可以使最开始大幅度更新的学习率变小，使学习率衰减。

class AdaGrad:

    """AdaGrad"""

    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None
        
    def update(self, params, grads):  #初始化时h不保存任意数，后续运行会生成与参数相同结构数组
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():  #公式代码实现
            self.h[key] += grads[key] * grads[key]   
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)  #1e-7是为了避免h为0时直接将0做分母

最开始会较大变动，但后面会按比例进行调整减少步伐。

5.1.3 Adam

Adam是15年新推出的方法，它是融合了Momentum和AdaGrad的方法，它也可以进行超参数的”偏置校正“。超参数包括学习率和另外两个系数。

上面推出的四种方法各有千秋，而且不存在可以适应所有问题情景的方法。

5.2 权重的初始值

权值衰减：减少权重参数（抑制过拟合的发生）。

在前面的代码中，我们可以注意到权重的生成公式为0.01*np.random.rand(10,100)，该代码会生成标准差为0.01符合高斯分布、结构为10*100、值区间为[0,1)的值。而为什么不将值全部设置为0呢，就是为了避免权重更新同步，会进行相同的更新，所以必须随机生成初始值。

若是将标准差0.01换为1生成初始值，我们来探究权重初始值对于隐藏层各层数据分布的影响。而在该神经网络可以改变激活函数和标准差来重复实验。

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def ReLU(x):
    return np.maximum(0, x)

def tanh(x):
    return np.tanh(x)
    
input_data = np.random.randn(1000, 100)  # 1000个数据
node_num = 100  # 各隐藏层的节点（神经元）数
hidden_layer_size = 5  # 隐藏层有5层
activations = {}  # 激活值的结果保存在这里

x = input_data

for i in range(hidden_layer_size):
    if i != 0:   #下一层的输入值会使用上一层activations的保存数据
        x = activations[i-1]

    # 改变初始值进行实验！
    w = np.random.randn(node_num, node_num) * 1
    # w = np.random.randn(node_num, node_num) * 0.01
    # w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
    # w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)

    a = np.dot(x, w)

    # 将激活函数的种类也改变，来进行实验！
    z = sigmoid(a)
    # z = ReLU(a)
    # z = tanh(a)

    activations[i] = z

# 绘制直方图
for i, a in activations.items():
    plt.subplot(1, len(activations), i+1)
    plt.title(str(i+1) + "-layer")
    if i != 0: plt.yticks([], [])
    # plt.xlim(0.1, 1)
    # plt.ylim(0, 7000)
    plt.hist(a.flatten(), 30, range=(0,1))
plt.show()

代码运行结果如下，我们可以发现五层神经神经网络里的激活值分布在两端，中间范围值分布稀少，这会导致激活值分布广度不够。所以下面的目的是要将激活值呈现相同的广度分布，而不是偏向

在Xavier Giorot论文里，提到过为了使各层的激活层呈现相同广度的分布，推导合适的权重，寻找到一种方法：如果前一层的节点数为n，则使用标准值为 $eq?%5Cfrac%7B1%7D%7B%5Csqrt%7Bn%7D%7D$ 的标准差进行初始化

node_num=100   #前一层的节点数
w=np.random.rand(node_num,node_num)/np.sqrt(node_num)

使用Xavier初始值后的激活值分布情况如下：

虽然分布情况较为斜歪，但广度分布比之前更广。

5.2.1 ReLU权重初始化

在使用ReLU激活函数时，使用ReLU匹配的初始值，由Kaiming He推荐，也称为”He初始值“

，与Xavier $eq?%5Cfrac%7B1%7D%7B%5Csqrt%7Bn%7D%7D$ 标准差不同的是，He初始值使用 $eq?%5Csqrt%7B%5Cfrac%7B2%7D%7Bn%7D%7D$ 。

使用标准差0.01即std=0.01的高斯分布时，各层的激活值很小，反向传播梯度也很小，学习慢；初始值为Xavier初始值会导致分布呈现递减情况，并且出现梯度消失的情况；He初始值的各层分布广度相同。

最后，激活函数为ReLU时，权重初始值使用He初始值，激活函数使用sigmoid和tanh等s型曲线函数时，初始值使用Xavier初始值。

5.3 Batch Normalization

简称Batch Norm：可以通过”强制性“调整激活值分布来使各层有适当的广度。它有以下的优点：可以快速学习、减少对初始值的依赖以及抑制过拟合。Batch Norm层会放在Affine和激活函数层之间。

Batch Norm会使mini-batch的数据分布进行均值为0、方差为1的正规化：

$eq?%5Cmu%20_%7BB%7D$ 是计算均值， $eq?%5Cdelta%20_%7BB%7D%5E%7B2%7D$ 是计算方差，而第三个式子是进行均值为0、方差为1的正规化，减少数据分布的偏向。分母的 $eq?%5Cvarepsilon$ 是为了避免为0。

正规化后的激活值，还会进行缩放和平移处理：

$eq?%5Cgamma$ 是缩放， $eq?%5Cbeta$ 是平移，最开始的 $eq?%5Cgamma%3D1$ 、 $eq?%5Cbeta%3D0$ ，后期可以通过学习调整。使用过Batch Norm的学习会更快，精确度提高快速，得益于Batch Norm可以使权重初始值不那么依赖初始值。

5.4 正规化

发生过拟合有两个主要原因，模型拥有大量参数或者训练数据少。为此，我们故意制造出拟合现象，复杂网络和少量数据。包括7层网络和300数据，，最后发现对于训练数据的精确度以及趋近于100%，但对于测试数据只有70%左右。

5.4.1 权值衰减和Dropout

权值衰减是一种常见的抑制过拟合方法，因为很多过拟合是由于权重参数过大导致的，所以权值衰减就是为了抑制权重过大，例如 $eq?loss+%5Cfrac%7B1%7D%7B2%7D%5Clambda%20%5Comega%20%5E%7B2%7D$ （损失函数加上权重的平方范数）， $eq?%5Clambda$ 是正则化的超参数，对应的导数便是 $eq?%5Clambda%20%5Comega$ 。加上权值衰减的学习过拟合程度减轻了，train和test识别精度差距变小。

Dropout：随机删除神经元。

前面我们介绍了损失函数加上权重的L2范数的权值衰减方法，不过在复杂模型里面效率就不太行了。这里介绍的是随机删除神经元方法Dropout，被删除的神经元将不会再参数信号传递。每传递一层就会随机删除神经元

5.5 验证超参数以及最优化

在神经网络中，除了权重偏置等参数，超参数也经常出现，比如神经元数量、batch大小、学习率以及权值衰减。

在验证数据里，训练数据用于学习，测试数据可以用于评估学习能力，但并不能用于评估超参数的性能（调整超参数必须使用专用的确认数据----验证数据）。所以，对于数据集，可以事先划分为三种数据，训练数据、测试数据和验证数据。

超参数的最优化是逐渐确定最优值所在区域：是从一开始大致设定一个范围，从这个范围中随机选出一个超参数，用这个采样到的值进行识别精度的评估，多次重复，根据结果缩小范围。就好像吃一个西瓜时，不清楚一个西瓜哪一块最甜，我们可以在不同地方都试一小块，凭甜度寻找最甜的区域。具体的操作步骤是先设定超参数范围，再从设定的超参数范围内随机抽样，然后对采样得到的超参数进行学习，通过验证数据评估精度，最后便是重复上面步骤，缩小范围。更精炼方法有贝叶斯最优化。

第6章卷积神经网络(CNN)

CNN被用于图像识别、语言识别等各种场合，在相关比赛也大多是基于CNN。

全连接：相邻层所有神经元都有连接，没有神经元被删除。

6.1 Convolution卷积层

在使用全连接层的时候，然后存在一个问题，就是会忽略形状，将输入的数据转化为同一纬度处理，所以有关形状相关信息无法获得，比如输入三维图像数据，导出的却不是三维的，但卷积层可以解决这一问题。而在CNN中，输入输出数据被称为特征图。

6.1.1 卷积运算——滤波器

卷积层进行的处理就是卷积算法，相当于图像处理中的“滤波器”。

如图所示，它将会依照次序逐一寻找输入数据中3*3形状的数据，并用各个位置上的对应数据进行相乘，然后并求和，而在CNN中，滤波器的参数对应的便是之前的权重。另外，求和值还可以加上偏置，会被应用到滤波器所有的元素上。然后我们可以观察输入输出数据以及滤波器的形状，可以发现输出数据形状是输入形状-滤波器形状+1。

6.1.2 填充

CNN中还有一些特有的术语，比如填充以及步幅。而填充便是向输入数据的周围扩张一圈固定数据（比如0），该操作便是填充。

按照之前发现的规律，可以发现输出数据变为了4*4。而填充的作用也显而易见，便是会以不变的空间大小继续传给下一层，而不至于数据空间越搞越小。

除了填充的介绍，步幅也是一个重要内容（应用滤波器的位置间隔）。例如步幅为2的操作：

不过我们发现，添加了步幅以后，输出数据的结构计算变得更加复杂，不过还是有迹可循。这里，我们假设输入数据为（H,W），滤波器大小为（FH,FW），输入数据为（OH,OW），填充为P，步幅为S（以幅度为S像素向外填充周围）。所以我们可以得到输出数据结构。

不过当用公式求输出数据大小时，可能会发生无法除尽问题，这里就会报错。

6.1.3 3维数据卷积运算

3维数据（3维分布是数据数量、数据高以及数据宽），而不同数据（或者称为不同）也可以称为不同通道。不过这里需要注意的是，有多少数据（通道）就要有多少数量的滤波器。

最后算出来的三维结果对应位置分布相加，得到输出数据。不过这里也出现了一个新问题，输入输出数据不仅结构不同，维度也不同。这里我们也有相应的解决方法，比如使用多个滤波器：

输入数据空间大小为（C,H,W），其中C为数据空间深度，(H,W)为数据面大小。因为需要滤波器有相同的通道数，所以滤波器大小也有C，空间结构为（output_channel滤波器数量,input_channel通道数,height高,width宽）。至于偏置，在两个方块相加时，要对输出数据按通道加上相同的偏置值，在同一通道里，对该通道的所有数据都加上偏置值，跟numpy的广播功能相似。

最后内容便是经典的批处理能力实现，跟以往一样，在输入数据前添加数据来这个值便可以实现，原理便是矩阵相乘需要对应结构相同，输入数据结构变为（N,C,H,W），变成了四维数据

6.2 Pool池化层

池化是缩小高、宽方向上的空间的运算。通常包括“MAX池化”也就是获取最大值的运算，一般来说。池化的窗口大小会和步幅设定成相同的值。

除了 “MAX池化”还有Average池化，与卷积层不同的是，池化层没有要学习的参数也说明没有滤波器，它只是从目标区域里面去的最大值或者平均值。而且通过池化运算，输入数据和输出数据的通道数并不会发生变化。而与卷积层相对应数相乘运算不同的是，池化层只找取最大值等，所以当输入数据发生偏小变化时，池化层输出结果不变，因此，对于输入数据的偏小数据具有鲁棒性（系统或者器件在不同的环境或者条件下，能够保持其功能或者性能的特性），会吸收输入数据的误差。

6.3 卷积层和池化层的代码实现

加上数据量的结构为四维，例如（10，1，28，28），它对应的是10个高28，宽28，通道为1的数据。

x=np.random.rand(10,1,28,28)
x.shape  #(10,1,28,28)

x[0].shape  #(1,28,28)可以访问第一个数据

6.3.1 im2col展开

im2col是一个函数（image to column），将输入数据展开为适合滤波器（权重），将四维变二维。其中，将单个输入数据（三维）展开为一维，单个数据展开为矩阵里的行，而对应的滤波器展开为矩阵的列。为什么这么展开呢，是因为矩阵相乘是第一个矩阵的行乘以第二个矩阵的列，与全连接的Affine层处理基本相同。相乘后的输出数据为二维数据，最后通过转换（reshape）为输出数据的大小。

6.3.2 卷积层代码实现

将卷积层设置为Convolution的类，这里便不提供卷积层反向传播代码：

class Convolution:
    def __init__(self, W, b, stride=1, pad=0):
        self.W = W
        self.b = b
        self.stride = stride
        self.pad = pad
        
        # 中间数据（backward时使用）
        self.x = None   
        self.col = None
        self.col_W = None
        
        # 权重和偏置参数的梯度
        self.dW = None
        self.db = None

    def forward(self, x):
        FN, C, FH, FW = self.W.shape
        N, C, H, W = x.shape
        out_h = 1 + int((H + 2*self.pad - FH) / self.stride)  #输出数据空间结构大小
        out_w = 1 + int((W + 2*self.pad - FW) / self.stride)

        col = im2col(x, FH, FW, self.stride, self.pad)   #输入数据展开
        col_W = self.W.reshape(FN, -1).T                 #滤波器展开，reshape会自动计算-1维度的元素个数，以使多维数组的元素个数前后一致
                                                         #比如 有750个数据的数组，利用reshape（10，-1）会转换为10*75的空间大小
        out = np.dot(col, col_W) + self.b                #输入数据与滤波器相乘，并加上偏置
        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)   #输出结果转换，transpose会通过指定索引，更改轴的顺序
                                                                       #原来顺序是（0，1，2，3）对应（N,H,W,C），改为了（N,C,H,W）
        self.x = x
        self.col = col
        self.col_W = col_W

        return out

6.3.3 池化层代码实现

池化层与卷积层一样，都是用im2col来展开输入数据。不过池化层在通道上是独立的，单独展开。

像这样展开后，只需对展开的矩阵求各行的最大值，并转化为合适的形状即可。

class Pooling:   #展开输入数据  求各行的最大值   转换为合适的输出大小
    def __init__(self, pool_h, pool_w, stride=1, pad=0):
        self.pool_h = pool_h
        self.pool_w = pool_w
        self.stride = stride
        self.pad = pad
        
        self.x = None
        self.arg_max = None

    def forward(self, x):
        N, C, H, W = x.shape
        out_h = int(1 + (H - self.pool_h) / self.stride)
        out_w = int(1 + (W - self.pool_w) / self.stride)
        #展开
        col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
                            # 高          宽           步幅        填充
        col = col.reshape(-1, self.pool_h*self.pool_w)

        #最大值
        out = np.max(col, axis=1)  #max函数与其它函数相反，axis=1是求行最大值
        #转换
        out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)

        return out

6.4 CNN的实现

卷积层和池化层实现后，便可以结合Affine和激活函数层来手搭手写数字识别CNN。

下面来看一下SimpleConvNet的初始化，可以分为三部分实现，第一部分便是参数初始化以及输出函数结构公式实现，然后便是各层权重偏置参数定义，最后便是依照流程结构生成必要的层。

class SimpleConvNet:
    """简单的ConvNet

    conv - relu - pool - affine - relu - affine - softmax
    
    Parameters
    ----------
    input_size : 输入大小（MNIST的情况下为784）
    hidden_size_list : 隐藏层的神经元数量的列表（e.g. [100, 100, 100]）
    output_size : 输出大小（MNIST的情况下为10）
    activation : 'relu' or 'sigmoid'
    weight_init_std : 指定权重的标准差（e.g. 0.01）
        指定'relu'或'he'的情况下设定“He的初始值”
        指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值”
    """
    def __init__(self, input_dim=(1, 28, 28), 
                 conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
                 hidden_size=100, output_size=10, weight_init_std=0.01):
        filter_num = conv_param['filter_num']   #滤波器的数量 
        filter_size = conv_param['filter_size'] #滤波器的大小
        filter_pad = conv_param['pad']          #填充
        filter_stride = conv_param['stride']    #步幅
        input_size = input_dim[1]

        conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
        pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))

        # 初始化权重    标准差乘以随机生成数
        self.params = {}
        self.params['W1'] = weight_init_std * \
                            np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
        self.params['b1'] = np.zeros(filter_num)
        self.params['W2'] = weight_init_std * \
                            np.random.randn(pool_output_size, hidden_size)
        self.params['b2'] = np.zeros(hidden_size)
        self.params['W3'] = weight_init_std * \
                            np.random.randn(hidden_size, output_size)
        self.params['b3'] = np.zeros(output_size)

        # 生成层
        self.layers = OrderedDict()   #有序字典OrderedDict，这里顺序要与流程结构相同
        self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
                                           conv_param['stride'], conv_param['pad'])
        self.layers['Relu1'] = Relu()
        self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
        self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
        self.layers['Relu2'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])

        self.last_layer = SoftmaxWithLoss()  #利用softmax求出输出概率值，并用标签求出损失函数

    def predict(self, x):
        for layer in self.layers.values():  #values：字典的值
            x = layer.forward(x)

        return x

    def loss(self, x, t):
        """求损失函数
        参数x是输入数据、t是教师标签
        """
        y = self.predict(x)
        return self.last_layer.forward(y, t)

类SimpleConvNet更多的定义函数便不具体展开。

卷积层和池化层是图像识别中必备的模块。CNN可以有效读取图像中的某种特性，可以对图像进行高精度识别。

6.5 CNN的可视化

CNN用到的卷积层通过观察边缘（颜色变化的分界线）和斑块（局部的块状区域），比如左边部分是白色右半部分是黑色情况下。学习后的滤波器会对水平或者垂直方向的边缘有响应。不过在整体上来看，第一层提取的边缘和斑块只不过是小部分或者说是低级信息，随着层次的叠加，提取的信息也会更加抽象。

conv1只能对边缘和斑块这样简单信息进行提取，不过到conv3和conv5便可以对纹理和物体部件响应，最后全连接层对物体的类别有响应，对更加复杂的物体部件有相应。

6.5.1 LeNet和AlexNet

LeNet是具有代表性的CNN，于1998年提出，是进行手写数字识别的网络。跟现在相比，LeNet使用的是sigmoid函数，现在的CNN使用ReLU函数。

AlexNet的网络结构和 LeNet相似，它堆叠有多个卷积层和池化层，最后有全连接输出结果。

第7章深度学习

这一章多是基于前面理论进行手写数字识别的实现以及内容的拓展，便不和前面内容一样展开讲。构建CNN网络，利用3*3小型滤波器的卷积层，全是ReLU激活函数以及使用Dropout层的全连接后面，这个网络还基于Adam的最优化，使用He初始值作为权重初始值。最后，这个网络的识别精度为99.38%，蕴含无限的可能。

进一步提高识别精度一直都是人们不懈的追求，而相关提高识别精度的技术有集成学习、学习率衰减、Data Augmentation（数据扩充）：可以通过施加微小变化比如旋转和移动来增加图像的数量。

书后面还有对加深层、以及由卷积层和池化层构成CNN的VGG、GoogLeNet和ResNet。这里还有基于GPU的高速化实现，通过分布式学习堆叠多个GPU来利用压倒性的计算能力来提高计算能力，100number of GPUs便可以提高56倍的高速化，不过对于分布式计算还有机器间通信和数据同步等问题。

深度学习还有物体检测的应用案例，从图像中确定物体的位置，并进行分类的问题。还有图像分割和图像标题生成，这些都是需要神经网络对对象的监督数据进行学习。

关于深度学习的未来，我只能说人有多大胆，地有多大产，任何技术以及知识都可能发掘出无限可能，而深度学习在现在热门应用便是自动驾驶和Deep Q-Network的强化学习。

字止与此，解析之旅到此结束。该博客也是我学习的一部分，挺像我期末周的学习方法，正常上课课是不带听的，到期末周便通过抄和练结合速通，大家也可以试试，我感觉挺有成就感。不过别看本博客字数众多，大部分都是代码占数，作为我的第一篇博客，也是有不一样的体验，也是构建世界观的一种经历。我还记得我高三我还经常跟我同桌说，我不求别的，能够体验一遍经历获得一份体验便是成就。