【算法笔记】有人看海，有人被爱，有人做不出 leetcode 第一题（二叉树专题 Part 5）

---

Day 15：二叉树

---

最大二叉树

---

题目链接：654. 最大二叉树 - 力扣（LeetCode）

文章讲解：代码随想录

视频讲解：又是构造二叉树，又有很多坑！| LeetCode：654.最大二叉树_哔哩哔哩_bilibili

题目建议：又是构造二叉树，昨天大家刚刚做完 中序后序确定二叉树，今天做这个 应该会容易一些， 先看视频，好好体会一下 为什么构造二叉树都是 前序遍历；

---

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        
    }
}

---

题目解析

---

1. 前序遍历构建：先构造根节点，再递归构建左右子树
2. 最大值作为根节点：每次在当前数组区间内找到最大值作为当前子树的根
3. 数组分割：根据最大值位置将数组分为左右两部分，分别构建左右子树

---

class Solution {
    int[] nums;
    public TreeNode constructMaximumBinaryTree(int[] nums1) {
        nums = nums1;
        return dfs(0, nums.length-1);
    }

    private TreeNode dfs(int start, int end){
        if(start > end){
            return null;
        }
        
        // err: maxVal 不能初始化为0, 否则如果使用元素都小于0, 导致错误的索引选择
        int maxVal = Integer.MIN_VALUE;  
        int index = 0;
        for(int i = start; i <= end; i++){
            if(nums[i] > maxVal){
                maxVal = nums[i];
                index = i;
            }
        }
        TreeNode root = new TreeNode(maxVal);
        root.left = dfs(start, index-1);
        root.right = dfs(index+1, end);
        return root;
    }
}

---

总结

---

1. 步骤：

   • 直接在原数组上操作，通过索引控制区间
   • 避免频繁创建新数组，提高效率
   • 使用区间[start, end]

2. 递归终止条件：

   • 当区间为空（start > end）时返回null

3. 时间复杂度：

   • 平均O(nlogn)，最坏O(n²)（当数组有序时）

4. 空间复杂度：

   • O(n)（递归栈空间）

---

合并二叉树

---

题目链接：617. 合并二叉树 - 力扣（LeetCode）

文章讲解：代码随想录

视频讲解：一起操作两个二叉树？有点懵！| LeetCode：617.合并二叉树

题目建议：这次是一起操作两个二叉树了， 估计大家也没一起操作过两个二叉树，也不知道该如何一起操作，可以看视频先理解一下。 优先掌握递归。

---

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        
    }
}

---

题目解析

---

• 递归函数： mergeTrees(TreeNode root1, TreeNode root2)
• 递归出口：如果一颗其中一个节点为空，返回另一个节点，这样能连接到另一个节点的子树
  • if (root1 == null) return root2;
  • if (root2 == null) return root1;
  • 该递归出口是本题的神来之笔，需要重点理解这个递归出口的作用；
• 重复子问题：处理当前节点的值，并且连接好左右子节点，然后向上返回处理好的节点；

---

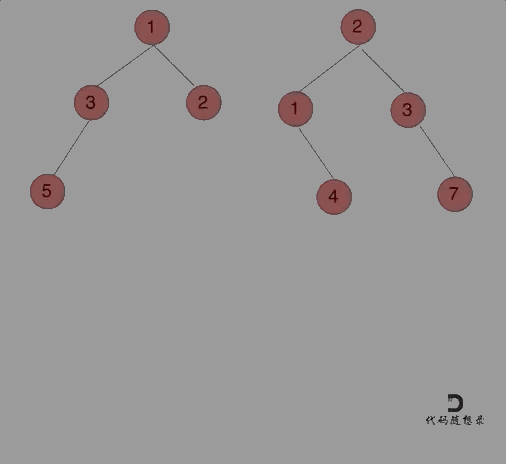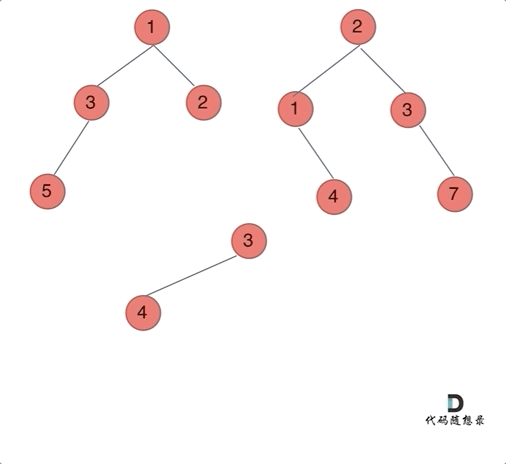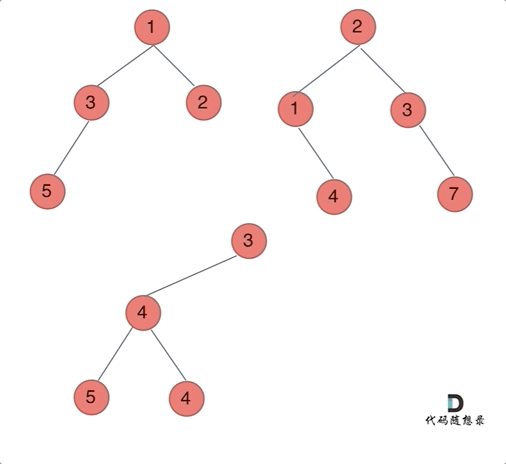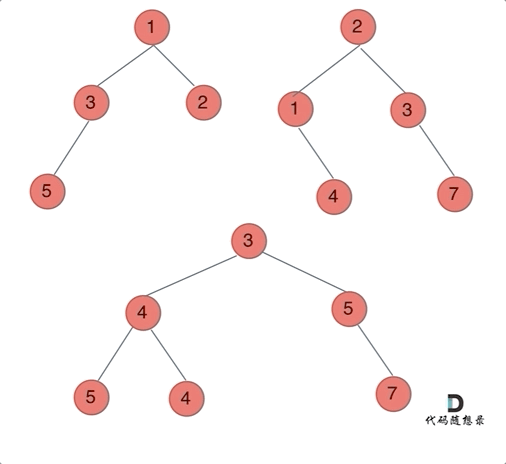
方法一：递归

---

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null) return root2;
        if (root2 == null) return root1;
        
        root1.val += root2.val;
        root1.left = mergeTrees(root1.left, root2.left);
        root1.right = mergeTrees(root1.right, root2.right);
        
        return root1;
    }
}

---

方法二：迭代（队列实现）

---

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null) return root2;
        if (root2 == null) return root1;
        
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root1);
        queue.offer(root2);
        
        while (!queue.isEmpty()) {
            TreeNode node1 = queue.poll();
            TreeNode node2 = queue.poll();
            
            node1.val += node2.val;
            
            if (node1.left != null && node2.left != null) {
                queue.offer(node1.left);
                queue.offer(node2.left);
            }
            
            if (node1.right != null && node2.right != null) {
                queue.offer(node1.right);
                queue.offer(node2.right);
            }
            
            if (node1.left == null && node2.left != null) {
                node1.left = node2.left;
            }
            
            if (node1.right == null && node2.right != null) {
                node1.right = node2.right;
            }
        }
        
        return root1;
    }
}

---

方法三：不修改原树结构（新建树）

---

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null) return root2;
        if (root2 == null) return root1;
        
        TreeNode root = new TreeNode(root1.val + root2.val);
        root.left = mergeTrees(root1.left, root2.left);
        root.right = mergeTrees(root1.right, root2.right);
        
        return root;
    }
}

---

总结

---

1. 递归思路：
   • 前序遍历方式处理节点
   • 直接修改 root1 的结构（或新建树）
   • 时间复杂度O(n)，空间复杂度O(n)
2. 迭代思路：
   • 使用队列层序遍历
   • 同时处理两棵树的对应节点
   • 时间复杂度O(n)，空间复杂度O(n)

提示：大多数情况下使用方法一即可，既高效又简洁。如遇到特别深的树（可能栈溢出），可考虑使用迭代法。

---

二叉搜索树中的搜索

---

题目链接：700. 二叉搜索树中的搜索 - 力扣（LeetCode）

文章讲解： 代码随想录

视频讲解：不愧是搜索树，这次搜索有方向了！| LeetCode：700.二叉搜索树中的搜索

题目建议：递归和迭代都可以掌握以下，因为本题比较简单， 了解一下二叉搜索树的特性

---

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        
    }
}

---

题目解析

---

二叉搜索树特性

---

• 左子树所有节点值 < 根节点值
• 右子树所有节点值 > 根节点值
• 左右子树也都是二叉搜索树

---

最优解法（利用BST特性）

---

1. 递归实现

---

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        // err: 如果当前节点为空, 或者当前节点的值等于目标值, 直接返回即可
        if(root == null || root.val == val){
            return root;
        }

        return root.val < val ? searchBST(root.right, val): searchBST(root.left, val);
        // err: root.val < val 是去右子树继续找, 不要弄反了
    }
}

---

2. 迭代实现

---

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        while(root != null){
            if(root.val == val)return root;
            root = (root.val > val ? root.left : root.right);
        }
        return root;
    }
}

---

三元运算符的语法是：

condition ? expressionTrue : expressionFalse

• condition 是一个布尔表达式，用于判断条件是否成立。
• expressionTrue 是当条件成立时执行的表达式。
• expressionFalse 是当条件不成立时执行的表达式。

root.val > val ? root = root.left : root = root.right;  // 错误, 后面不能是赋值操作

root = (root.val > val ? root.left : root.right); // 正确使用方法

---

普通二叉树解法（对比参考）

---

1. 递归实现

---

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) return root;
        TreeNode left = searchBST(root.left, val);
        return left != null ? left : searchBST(root.right, val);
    }
}

---

2. 迭代实现（使用栈）

---

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null) return null;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node.val == val) return node;
            if (node.right != null) stack.push(node.right);
            if (node.left != null) stack.push(node.left);
        }
        return null;
    }
}

---

总结

---

1. BST搜索优势：

   • 利用有序性可确定搜索方向
   • 无需遍历所有节点，效率更高

2. 时间复杂度：

   • BST最优解：平均O(logn)，最坏O(n)（退化成链表时）
   • 普通二叉树解：O(n)

3. 空间复杂度：

   • 递归：O(h)，h为树高
   • 迭代：BST最优解O(1)，普通解法O(n)

4. 实现建议：

   • 优先使用BST特性解法
   • 迭代法通常效率更高
   • 普通二叉树解法仅作对比参考

---

验证二叉搜索树

---

题目链接：98. 验证二叉搜索树 - 力扣（LeetCode）

文章讲解：代码随想录

视频讲解：你对二叉搜索树了解的还不够！ | LeetCode：98.验证二叉搜索树

题目建议：遇到搜索树，一定想着中序遍历，这样才能利用上特性。 但本题是有陷阱的，可以自己先做一做，然后在看题解，看看自己是不是掉陷阱里了。这样理解的更深刻。

---

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        
    }
}

---

题目解析

---

方法一：上下界递归（最佳性能）

---

• 关键易错点：
  1. 每次递归只检查当前节点与直接子节点的关系；
  2. 没有验证整个左子树都小于当前节点，整个右子树都大于当前节点；
     

---

• 递归出口：遍历到空节点时，返回 true

---

• 递归函数：dfs(TreeNode root, Long minVal, Long maxVal )
  

---

• 重复子问题（验证整个左子树都小于当前节点，整个右子树都大于当前节点）：
  1. root.val <= minVal、root.val >= maxVal，如果有一个符合，返回 false
  2. 继续判断左子树 root.left.val 、 minVal 、 root.val
  3. 继续判断右子树 root.right.val、root.val、maxVal

---

class Solution {
    public boolean isValidBST(TreeNode root) {
        return dfs(root, Long.MIN_VALUE, Long.MAX_VALUE);
        // err: 如果使用 Integer, root = [2147483647] 一个节点时会返回 false
    }

    private boolean dfs(TreeNode root, long minVal, long maxVal){
        if(root == null){
            return true;
        }

        if(root.val >= maxVal || root.val <= minVal){  
            // err: 等于的时候也应该是错的, 并且不是 &&
            return false;
        }

        return dfs(root.left, minVal, root.val) && dfs(root.right, root.val, maxVal);
    }
}

---

方法二：中序遍历+数组验证

---

class Solution {
    private List<Integer> list = new ArrayList<>();

    public boolean isValidBST(TreeNode root) {
        traversal(root);
        for (int i = 1; i < list.size(); i++) {
            if (list.get(i) <= list.get(i-1)) return false;
        }
        return true;
    }

    private void traversal(TreeNode root) {
        if (root == null) return;
        traversal(root.left);
        list.add(root.val);
        traversal(root.right);
    }
}

---

方法三：递归中序遍历（推荐）

---

class Solution {
    private TreeNode prev = null;

    public boolean isValidBST(TreeNode root) {
        if (root == null) return true;
        if (!isValidBST(root.left)) return false;
        if (prev != null && prev.val >= root.val) return false;
        prev = root;
        return isValidBST(root.right);
    }
}

---

方法四：迭代中序遍历

---

class Solution {
    public boolean isValidBST(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode prev = null;
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            if (prev != null && prev.val >= root.val) return false;
            prev = root;
            root = root.right;
        }
        return true;
    }
}

---

总结

---

1. BST验证核心：中序遍历结果必须严格递增

2. 常见陷阱：

   • 仅比较左右子节点（错误）
   • 处理Integer.MIN_VALUE边界情况

3. 方法对比：

   • 方法一：最佳性能解法（O(n)时间，O(1)空间）
   • 方法二：直观但需要额外空间
   • 方法三：最优递归解法
   • 方法四：最优迭代解法

提示：推荐使用方法一或方法二，代码简洁且效率高。使用方法一时注意用 long 类型处理边界值。

---