为什么浮点数会有精度丢失?(数学角度分析)

最新推荐文章于 2025-05-18 19:14:41 发布

解析几何太难啦QAQ

最新推荐文章于 2025-05-18 19:14:41 发布

阅读量1.1k

点赞数 51

文章标签：算法数论离散数学集合论进制

本文链接：https://blog.csdn.net/2402_85728830/article/details/147970441

版权

这篇文章属于后传，前传中分析了整数多进制的意义和一些规则，扩充数系到了整数集，并证明了一个重要命题：一个p进制整数唯一对应一个q进制整数。本文将把多进制数系扩充到小数，并由此分析为什么浮点数会有精度丢失的问题。

经典永流传：

一. 多进制小数

其实这也很好理解，比如我说一个数字比1小，小数点后仅三个数，它们是1，2，3，这个数是多少呢？你肯定知道，是：

$1\cdot 10^{-1}+2\cdot 10^{-2}+3\cdot 10^{-3}=0.123$

同理，二进制小数 $0.101_{(2)}$ 是多少呢？就是加权展开：

$1\cdot 2^{-1}+0\cdot 2^{-2}+1\cdot2^{-3}=0.625$

在前传中，我们指出，一个q进制整数有唯一表示形式 $\sum_{i=0}^{\infty }d_{i}\cdot q_{i},d_{i}\in \left \{ \right.0,1,2\cdots q-1\left. \right \}$ 。现在扩充到了小数部分，则 $i$ 的负无穷取值也就解锁了，新的表示形式是：

$\sum_{i=-\infty}^{\infty}d_{i}\cdot q_{i},d_{i}\in \left \{ \right.0,1,2\cdots,q-1\left. \right \}$

二. 为什么会有精度丢失？

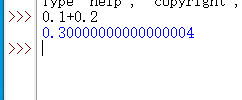
我们平时计算用的是十进制，因为人有10根手指，这符合我们的直觉。但是，计算机是二进制的世界，任何数据最终也是以二进制存储的。也就是说，在将10进制的浮点数转换为2进制小数储存的时候，出现了舍入误差。下面举个例子：

十进制数0.1，它的二进制表示可以这样计算（为了节省篇幅，这个计算方法我们不证）：

$0.1\times 2=0.2$ ，整数位是0，取小数继续计算：

$0.2\times 2=0.4$ ，整数位是0，继续取小数：

$0.4\times2=0.8$ ，整数位是0，继续：

$0.8\times 2=1.6$ ，整数位是1，取小数0.6继续：

$0.6\times2=1.2$ ，整数位是1，取小数0.2。

这已经和第二步一样了(取0.2)，所以开始循环，下面将会出现0011 0011……

因此： $0.1_{(10)}=0.00011001100110011\cdots_{(2)}$

可以看到，简单的0.1的二进制形式竟然是循环小数！但是，我们不可能在计算机里存储一个无限循环小数，只能取它的一个近似值，比如 $0.000110011_{(2)}$ 。但是，一旦我们这么做了，它就只能是0.1的一个近似值，而不是精确值。这就是精度丢失的原理。

三. 什么时候出现无限小数？

下面我们采取和前传一样的逐步推进思路。

命题1：无理数在任何整数多进制都是无理数

证明：无理数指的是不能表示为两个质因数之商的数。如果可以这样表示，把上下因数全部转换进制并适度化简，仍是质因数之商，即有理数转换进制仍是有理数。因此，任何多进制中，如果一个无理数被写成了质因数之商，它就肯定可以化成10进制有理数，这与它本身是无理数矛盾。所以无理数在任何整数多进制都是无理数，完毕。

命题2：一个q进制小数和一个10进制小数一一对应（双射）

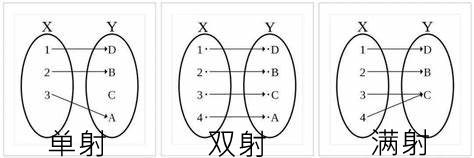
证明：

这个命题我们不严格证明，因为我没有想到不用“势”之类高级理论证明它的办法。

仿照前传的过程，由不同进制小数的转换规则可知，“一个q进制小数唯一对应一个10进制小数”和“一个10进制小数唯一对应一个q进制小数”都是成立的，所以它们是双向单射，也就存在双射（具体过程参考前传）

下面的命题是本文的重点：

命题3：一个10进制小数可以写成有限位的2进制小数，当且仅当它具有以下形式：

$x_{(10)}=\frac{a}{2^{n}},a,n\in\mathbb{Z}$

先不证：

在数论中有一个定理，命题3是它的特例而已。

定理(进制表示定理)：

一个分数在某个进制中具有有限小数表示，当且仅当该分数的分母（化为最简形式后）的质因数分解仅包含该进制的基数的质因数。

解释浮点数精度丢失有命题3就够了，下面我们来证明它，需要用到前传中的命题。

四. 证明何时位数有限的命题

命题：一个10进制小数可以写成有限位的2进制小数，当且仅当它具有以下形式：

$x_{(10)}=\frac{a}{2^{n}},a,n\in\mathbb{Z}$

证明：

其实，这是一个充要条件：

10进制数可以写成特定形式 $\Leftrightarrow$ 2进制数有限

为了证明它，只要证明必要性和充分性即可。

必要性：

假设二进制数有限，则从某个小数位n开始，二进制小数的数位上全是0，因此：

$x_{(2)}=\sum_{i=-\infty}^{\infty}d_{i}\cdot 2^{i}=\sum_{i=n}^{\infty}d_{i}\cdot 2^{i}=\sum_{i=0}^{\infty}d_{i}\cdot 2^{i}+\sum_{i=n}^{-1}d_{i}\cdot 2^{i}$

其中 $\sum_{i=0}^{\infty}d_{i}\cdot 2^{i}$ 是整数部分，肯定可以写成那种形式。对于小数部分，有：

$\sum_{i=n}^{-1}d_{i}\cdot 2^{i}=\frac{d_{1}}{2}+\frac{d_{2}}{2^{2}}+\cdots+\frac{d_{n}}{2^{n}}=\frac{d_{1}\cdot2^{n-1}}{2^{n}}+\frac{d_2\cdot2^{n-2}}{2^{n}}+\cdots+\frac{d_{n}}{2^{n}}$

$=\frac{2^{n-1}\cdot d_{1}+2^{n-2}\cdot d_{2}+\cdots+d_{n}}{2^{n}}$ ，也可以写成那种形式，所以整个转换后的小数都可以写成这种形式，必要性得证。

充分性：

假设10进制数满足 $x_{(10)}=\frac{a}{2^{n}},a,n\in\mathbb{Z}$ ，由于a是整数，利用前传中的命题：一个q进制整数唯一对应一个p进制整数，可以把a展开成唯一的二进制加权和形式：

$x_{(10)}=\frac{a}{2^{n}}=\frac{\sum_{i=0}^{\infty}d_{i}\cdot 2^{i}}{2^{n}}$

然后让式中每一个2的方幂项除以 $2^{n}$ ，可得：

$x_{(10)}=\sum_{i=-n}^{\infty}d_{i}\cdot q^{i}$

这显然是一个有限位的二进制数，小数位最大到 $2^{n}$ 分位，充分性得证。

因此，这两个条件彼此互为充要条件，命题证毕。

五. 验证结论

就比如0.1，它可以写成 $\frac{1}{10}$ ，分母不是 $2^{n}$ 类，我们前面也发现它转换成2进制是无限小数了。

再比如，二进制数0.101，我们已经算出它是0.625，而 $0.625=\frac{5}{8}=\frac{5}{2^{3}}$ ，确实是我们研究的那种形式。

再比如，我瞎选一个满足形式的奇葩十进制数 $\frac{1145}{2^{10}}\approx 1.118164063\dots$ ，经计算它是：

$1.0001111001_{(2)}$ ，确实是有限小数，且最大小数位是 $2^{10}$ 分位。

六. 其它内容

我们了解到，浮点数精度丢失不是编程语言的问题，也不是我们的问题，而是数学上进制转换的一个基本问题。

Python官方文档也讨论了这个情况，下面指一下路：

浮点算术：争议和限制https://docs.python.org/zh-cn/3.13/tutorial/floatingpoint.html在精度要求不特别高的时候，IEEE 754 binary64 "双精度" 值完全够用了。而严格要求精度的地方，也有大量科学计算工具和库可以使用，因此不必太担心这种误差。