CSC3100【Heap】

原创已于 2025-11-11 10:30:25 修改 · 563 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #c++

于 2025-11-10 23:33:19 首次发布

csc3100 专栏收录该内容

3 篇文章

订阅专栏

一，引入：Priority Queue

A priority queue is a data structure that stores elements with priority values and processes them in an order based on these values, rather than the order in which they were inserted.
◦ The priority value of an element determine its order of service

① Priority queue property:

◦ For any two elements in the queue, x and y, if x has a lower priority value than y, then x will be deleted before y

二，Priority queue operations

◦ Insert: insert a new element into a priority queue
◦ DeleteMin: delete the element with minimum priority value from
a priority queue
◦ Build: given a set of elements with their priority values, build a
priority queue
◦ IsFull: test whether a priority queue is full or not
◦ IsEmpty: test whether a priority queue is empty or not

三，binary heap特点&分类

(A) Structure property

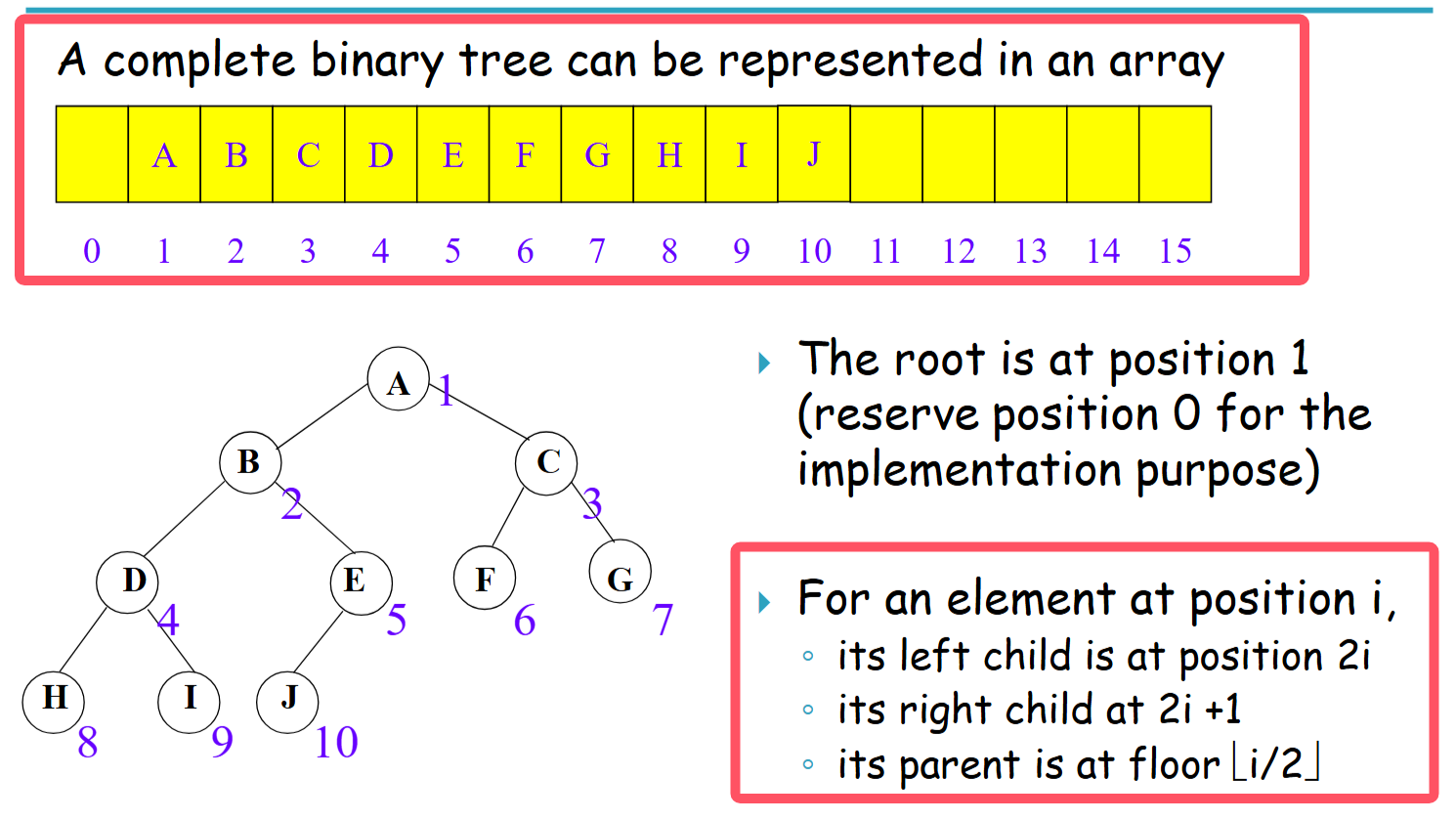
A heap is a complete binary tree. A binary tree that is completely filled, except at the bottom level,which is filled from left to right.

（B) Heap order property

◦ The value at any node should be smaller than (or equal to)all of its descendants (guarantee that the node with the minimum value is at the root)
◦ It is a recursive requirement

分类：

Min-heap ，Max-heap

四，The differences between BST和heap

特性	二叉搜索树（BST）	二叉堆（Binary Heap）
结构	二叉树，可能不完全	完全二叉树
节点值的关系	左子树 < 根 < 右子树	父节点与子节点满足堆性质（最大堆或最小堆）
用途	快速查找、插入和删除	实现优先队列，快速获取最大值或最小值
时间复杂度	查找、插入、删除：`O(log n)`（平衡时）	插入、删除：`O(log n)`
存储方式	通常用指针实现	通常用数组实现

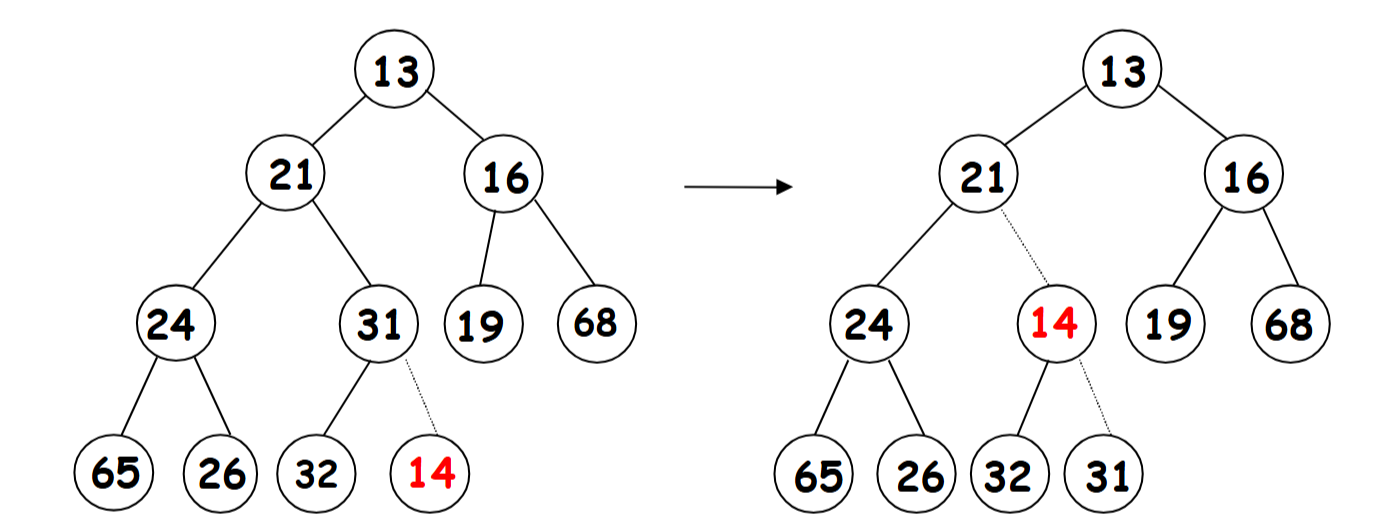
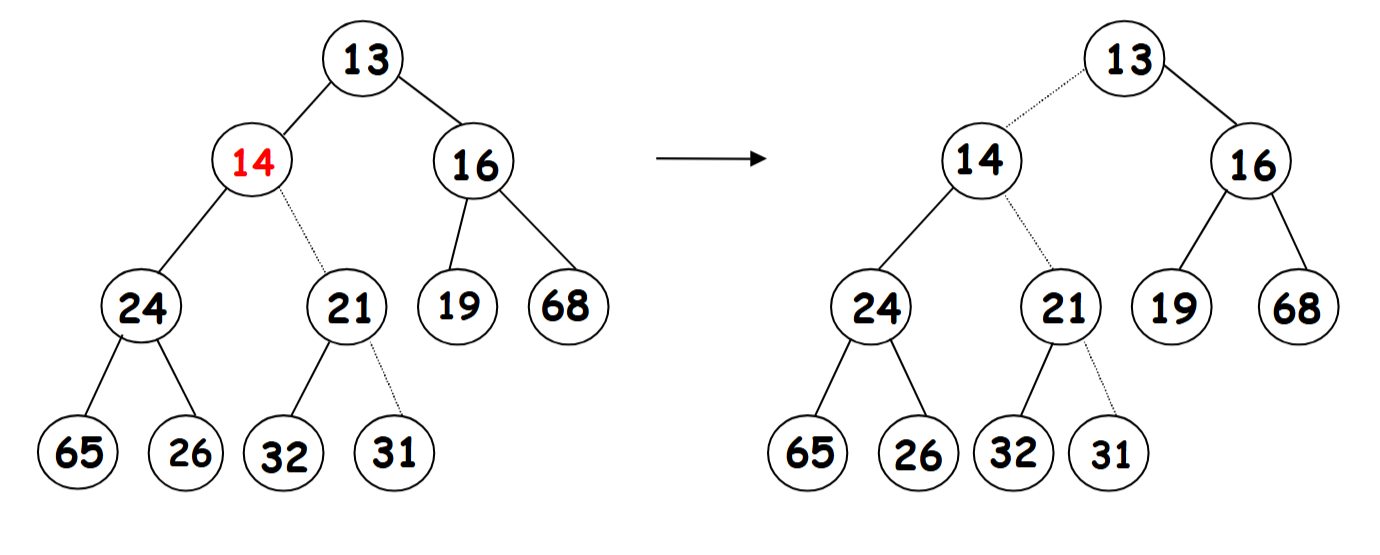
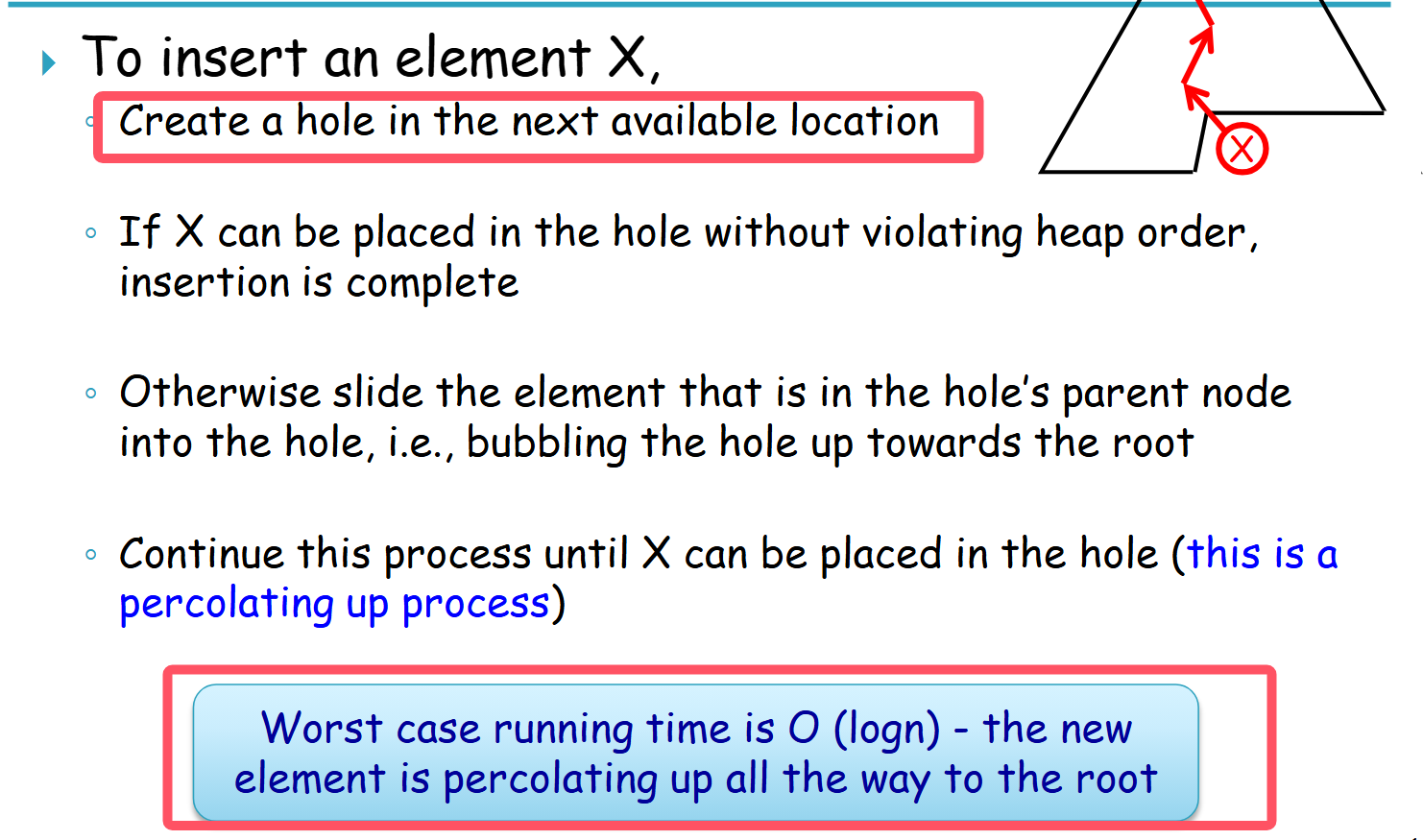
五，insertion

（如何insert？先插入最新的位置，然后在慢慢modify。将数字和parent比较，如果数字更小，那么就和parent交换位置。）

#include <iostream>
#include <stdexcept>
using namespace std;

class ElementType {
public:
    int priority;
    string data;

    ElementType(int priority, string data) {
        this->priority = priority;
        this->data = data;
    }

    bool isHigherPriorityThan(const ElementType& e) const {
        return priority < e.priority; // Assuming lower priority value means higher priority
    }
};

class BinaryHeap {
private:
    int currentSize;
    int capacity;
    ElementType** arr; // Array of pointers to ElementType

public:
    BinaryHeap(int capacity) {
        this->capacity = capacity;
        currentSize = 0;
        arr = new ElementType*[capacity + 1]; // Allocate memory for the heap array
    }

    ~BinaryHeap() {
        for (int i = 1; i <= currentSize; ++i) {
            delete arr[i]; // Free memory for each element
        }
        delete[] arr; // Free memory for the array
    }

    bool isFull() const {
        return currentSize == capacity;
    }

    void insert(const ElementType& x) {
        if (isFull()) {
            throw overflow_error("Overflow");
        }

        // Percolate up
        int hole = ++currentSize;
        while (hole > 1 && x.isHigherPriorityThan(*arr[hole / 2])) {
            arr[hole] = arr[hole / 2];
            hole /= 2;
        }
        arr[hole] = new ElementType(x.priority, x.data); // Insert the new element
    }

    void printHeap() const {
        for (int i = 1; i <= currentSize; ++i) {
            cout << "(" << arr[i]->priority << ", " << arr[i]->data << ") ";
        }
        cout << endl;
    }
};

void insert(const ElementType& x) {
if (isFull()) {
throw overflow_error("Overflow");
}
int hole = ++currentSize;
while (hole > 1 && x.isHigherPriorityThan(*arr[hole / 2])) {
arr[hole] = arr[hole / 2]; //如果说x有更高的优先级那么就将父节点的值改成当前节点
hole /= 2;//并且把hole的位置更新（相当于更新要insert的值的index）
}
arr[hole] = new ElementType(x.priority, x.data); //通过while循环找到index之后，将数值放进去
}

六，DeleteMin

（delete min的思路：删除root，将最新的元素放到root，将root和两个孩子比较，交换：和最小的孩子。直到root小于两个孩子。）、

#include <iostream>
#include <stdexcept>
using namespace std;

class ElementType {
public:
    int priority;
    string data;

    ElementType(int priority, string data) {
        this->priority = priority;
        this->data = data;
    }

    bool isHigherPriorityThan(const ElementType& e) const {
        return priority < e.priority; // Assuming lower priority value means higher priority
    }
};

class BinaryHeap {
private:
    int currentSize;
    int capacity;
    ElementType** arr; // Array of pointers to ElementType

public:
    BinaryHeap(int capacity) {
        this->capacity = capacity;
        currentSize = 0;
        arr = new ElementType*[capacity + 1]; // Allocate memory for the heap array
    }

    ~BinaryHeap() {
        for (int i = 1; i <= currentSize; ++i) {
            delete arr[i]; // Free memory for each element
        }
        delete[] arr; // Free memory for the array
    }

    bool isEmpty() const {
        return currentSize == 0;
    }

    string deleteMin() {
        if (isEmpty()) {
            return ""; // Return empty string if the heap is empty
        }

        string data = arr[1]->data; // Get the data of the root (minimum element)
        delete arr[1]; // Free memory for the root element
        arr[1] = arr[currentSize--]; // Replace root with the last element
        percolateDown(1); // Restore heap property
        return data;
    }

private:
    void percolateDown(int hole) {
        int child;
        ElementType* tmp = arr[hole]; // Store the element to be moved down
        while (hole * 2 <= currentSize) {
            child = hole * 2; // Left child index
            // Check if right child exists and has higher priority than left child
            if (child != currentSize && arr[child + 1]->isHigherPriorityThan(*arr[child])) {
                child++;
            }
            // If the child has higher priority than the current element, move the child up
            if (arr[child]->isHigherPriorityThan(*tmp)) {
                arr[hole] = arr[child];
            } else {
                break; // Stop if the heap property is satisfied
            }
            hole = child; // Move down to the child's position
        }
        arr[hole] = tmp; // Place the element in its correct position
    }
};

string deleteMin() {
if (isEmpty()) {
return ""; // Return empty string if the heap is empty
}

string data = arr[1]->data; // 获取root的数据
delete arr[1]; // 释放root的内存
arr[1] = arr[currentSize--]; // 将最后一个数据填到root里面
percolateDown(1); // Restore heap property
return data;
}

void percolateDown(int hole) {
int child;
ElementType* tmp = arr[hole]; //存储位置在最后的数据
while (hole * 2 <= currentSize) { //对于hole节点来说，他的子节点位置是hole*2，检查有无左节点
child = hole * 2; //孩子指针先指向左节点。如果下述if都不成立那么，在没有右子节点或左子节点优先级更高的情况下，child 会指向左子节点。

if (child != currentSize && arr[child + 1]->isHigherPriorityThan(*arr[child])) {
child++;
} //假如左节点不是最后一个元素并且右节点优先级别比左节点高

if (arr[child]->isHigherPriorityThan(*tmp)) {//如果右节点比父母优先级别还高
arr[hole] = arr[child];//那么父母的hole（index）就直接变成孩子
} else {
break; // Stop if the heap property is satisfied
}
hole = child; // Move down to the child's position
}
arr[hole] = tmp; // Place the element in its correct position
}
};

七，Binary heap construction

①method

逐个插入法：
- 每次插入后通过“上浮”调整堆结构。
- 时间复杂度为 O(n log n)，效率较低。
批量构建法：
- 先批量插入所有节点，再从底向上调整堆结构。
- 时间复杂度为 O(n)，效率更高。

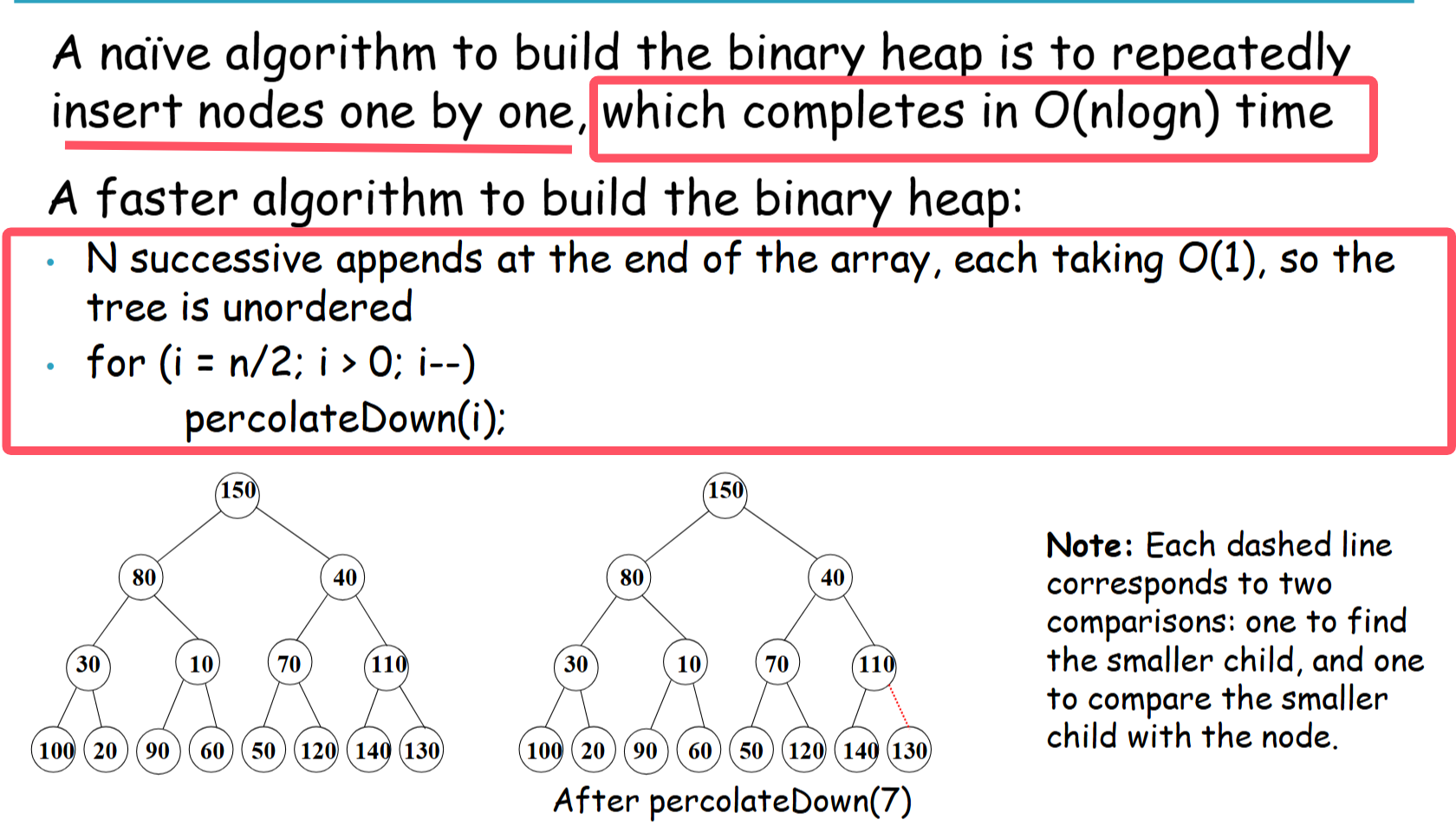
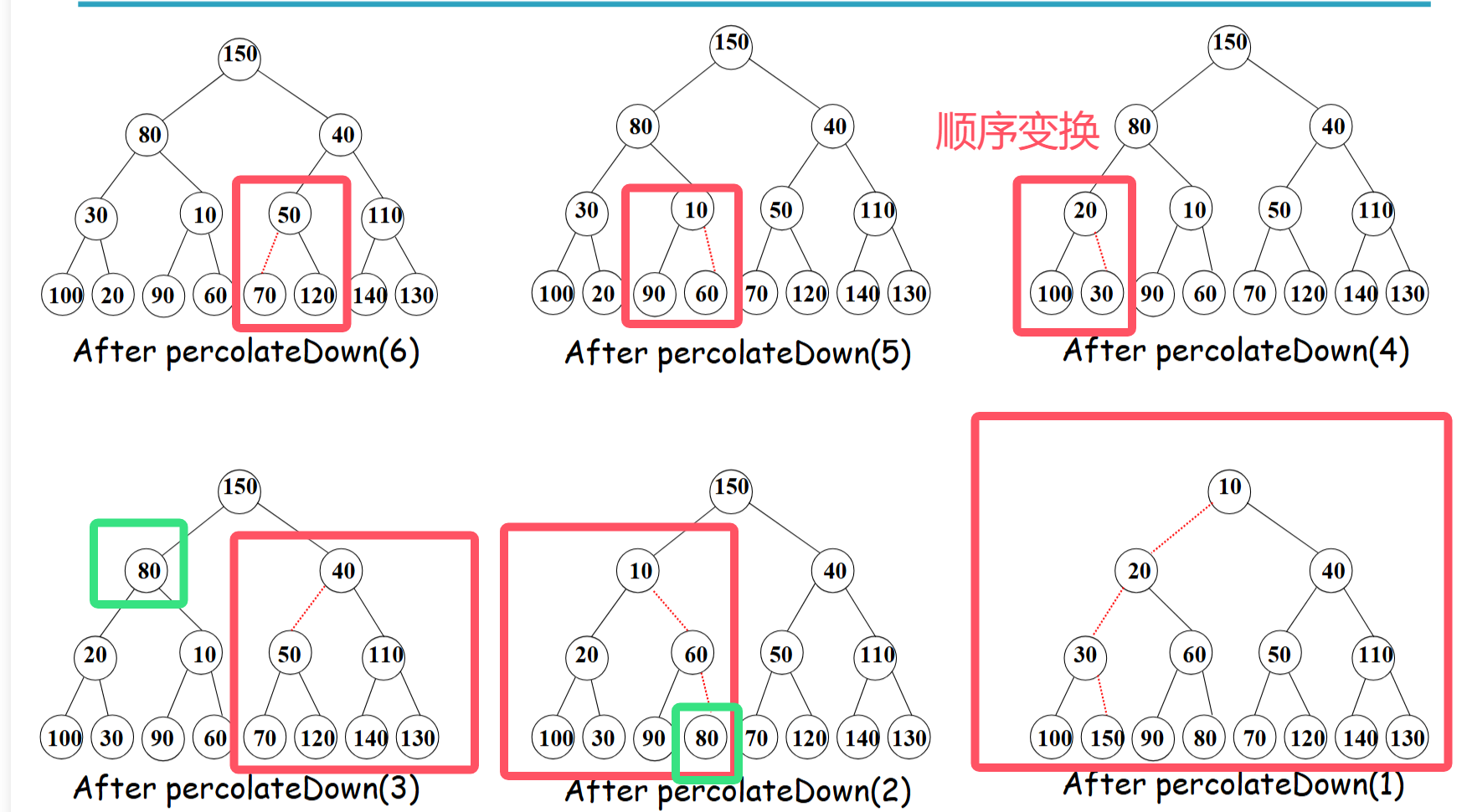
②complexity of building a heap

八，heapsort

（首先先构造一个maxheap，然后每次都删除root（root是最大值），删除root之后都把root存储到一个array里面即可。【然后调用percolate函数，重新构建maxheap，对n个元素操作，所以时间复杂度是nlogn。这个不是稳定的，因为相同的元素在sort之后位置会被改变】）

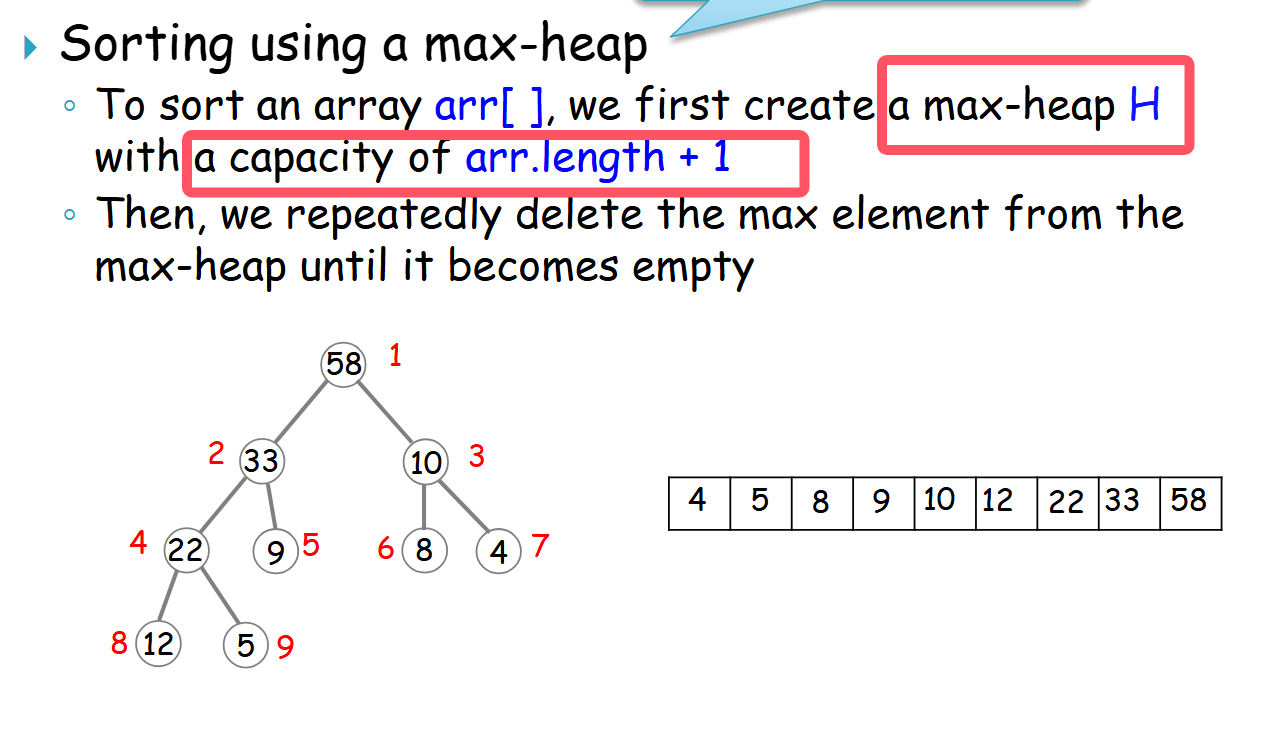
caution：注意，with a capacity of arr.length + 1

1. 初始数组

假设我们有一个数组 arr[]，长度为 9，包含以下元素：

arr[] = {58, 33, 10, 22, 9, 8, 4, 12, 5}

目标是对这个数组进行排序。

2. 创建 Max-Heap

为了使用堆排序，我们需要将数组转换为一个 Max-Heap。堆通常使用数组来存储数据，并且从 索引 1 开始存储元素，而不是从索引 0 开始。

为什么从索引 1 开始存储？

堆的父子节点关系在索引从 1 开始时更加简单：
- 父节点索引：i
- 左子节点索引：2 * i
- 右子节点索引：2 * i + 1
如果从索引 0 开始存储，计算关系会变得复杂。

堆的容量

数组 arr[] 的长度是 9。
为了从索引 1 开始存储元素，堆的容量需要是 arr.length + 1，即 10。
堆的数组表示为：
heap[] = [_, 58, 33, 10, 22, 9, 8, 4, 12, 5] 注意：
- 索引 0 的位置是空的（用 _ 表示）。
- 索引 1 到索引 9 存储了所有元素。