普通筛&埃氏筛&线性筛【详解+模板+例题】

引言

质数筛法是数论中的基础算法，用于高效求出一定范围内的所有质数。本文将详细介绍三种经典筛法，分析它们的原理、实现和效率差异。

1. 普通筛法

基本思想

对每个数进行暴力判断，检查是否能被小于它的数整除。

算法特点

• 时间复杂度：O(n√n)
• 空间复杂度：O(1)
• 优点：实现简单
• 缺点：效率极低

代码实现

#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
int primes[N];
int Is_prime(int x)//判断是否为素数
{
	if(x<2)//小于2的都不是素数
	return 0;
	for(int i=2;i<=sqrt(x);i++)
	{
		if(x%i==0)//判断是否能被小于它的数整除
		return 0;
	}
	return 1;
}
int main()
{
	int n,k=0;
	cin>n;
	for(int i=1;i<=n;i++)
	{
		if(Is_prime(i))
		prime[k++]=i;//记录在质数数组中
	}
	return 0;
}

2.埃氏筛法

基本思想

从2开始，将每个质数的倍数标记为合数。

算法特点

• 时间复杂度：O(n log log n)
• 空间复杂度：O(n)
• 优点：比普通筛快很多
• 缺点：存在重复标记

优化技巧

• 从i²开始标记

• 只筛奇数（空间减半）

代码实现

#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
bool st[N];//状态数组
int primes[N],n,ans=0;//primes存质数
void get_primes()
{
	for(int i=2;i<=n;i++)
	{
		if(st[i])continue;//不是质数下面的不用进行了
		primes[ans++]=i;//如果是质数就存进去
		for(int j=i;j<=n;j+=i)//将质数的倍数都标记为true 
		st[j]=true;
	}
}
int main()
{
	cin>>n;
	get_primes();
	return 0;
 } 

3.欧拉筛（线性筛）

基本思想

每个合数只被它的最小质因数筛掉，确保O(n)时间复杂度。

算法特点

• 时间复杂度：O(n)

• 空间复杂度：O(n)

• 优点：理论最优复杂度

• 缺点：实现稍复杂

关键点

• 维护质数列表

• 当i % primes[j] == 0时break

代码实现

#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
bool st[N];//状态数组，初始为fasle
int primes[N],n,ans=0;
void get_primes()
{
	for(int i=2;i<=n;i++)
	{
		if(!st[i])primes[ans++]=i;//如果是素数就存进去
		for(int j=0;primes[j]<=n/i;j++)//避免重复标记
		{
			st[primes[j]*i]=true;//将质数的倍数标记为true
			if(i%primes[j]==0)//停止条件
			break;
		}
	 }
}
int main()
{
	cin>>n;
	get_primes();
	return 0;
 } 

4.算法对比

对比维度	普通筛法	埃拉托斯特尼筛法（埃氏筛）	欧拉筛（线性筛）
时间复杂度	O(n√n)	O(n log log n)	O(n)
空间复杂度	O(1)	O(n)	O(n)
核心思想	暴力检查每个数的因数	标记质数的倍数为合数	每个合数只被最小质因数筛除
重复操作	无优化	会重复标记某些合数	无重复标记
实现难度	非常简单	较简单	较复杂
最佳适用场景	n ≤ 10⁴	10⁴ < n ≤ 10⁷	n > 10⁷
扩展功能	仅能筛质数	仅能筛质数	可记录最小质因数

5.例题训练

(1).P3383 【模板】线性筛素数

P3383 【模板】线性筛素数

题目

本题已更新，从判断素数改为了查询第 $k$ 小的素数。

提示：本题输入输出、运算数据量较大。

• 对于 C++ 语言，如果你使用 cin 来输入输出，建议使用 std::ios::sync_with_stdio(0) 来加速，同时使用 '\n' 换行输出。
• 对于 Java 语言，使用线性筛并且优化输入输出，也可以在规定时限内通过本题，但是时限可能较紧张。
• 对于 Python 语言，语言性能差异较大，需要使用到 numpy 库的数组以替代列表，且使用埃氏筛法，依然可以在合适的时间和内存消耗下通过本题。

题目描述

如题，给定一个范围 $n$，有 $q$ 个询问，每次输出第 $k$ 小的素数。

输入格式

第一行包含两个正整数 $n,q$，分别表示查询的范围和查询的个数。

接下来 $q$ 行每行一个正整数 $k$，表示查询第 $k$ 小的素数。

输出格式

输出 $q$ 行，每行一个正整数表示答案。

输入输出样例 #1

输入 #1

100 5
1
2
3
4
5

== 输出 #1==

2
3
5
7
11

说明/提示

【数据范围】
对于 $100\%$ 的数据，$n=10^8$，$1\le q\le 10^6$，保证查询的素数不大于 $n$。

Data by NaCly_Fish.

解题思路

这是一个质数筛的模板题，因为这道题n的范围最大时10⁸,我们用欧拉筛来写！

代码实现

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
using namespace std;
const int N=1e8+6;
bool st[N];
int primes[N];
int n,q,k,ans=0;
int main()
{
	IOS;
	cin>>n>>q;
	for(int i=2;i<=n;i++)
	{
		if(!st[i])primes[ans++]=i;
		for(int j=0;primes[j]<=n/i;j++)
		{
			st[primes[j]*i]=true;
			if(i%primes[j]==0)
			break;
		}
	}
	while(q--)
	{
		cin>>k;
		cout<<primes[k-1]<<endl;
	}
	return 0;
}

(2)-P3912 素数个数

P3912 素数个数

题目

求 $1,2,\cdots ,N$ 中素数的个数。

== 输入格式==

一行一个整数 $N$。

== 输出格式==

一行一个整数，表示素数的个数。

== 输入输出样例 #1==

== 输入 #1==

10

== 输出 #1==

4

== 说明/提示==

对于 $40\%$ 的数据，$1\le N\le 10^6$。

对于 $80\%$ 的数据，$1\le N\le 10^7$。

对于 $100\%$ 的数据，$1\le N\le 10^8$。

解题思路

这题也很简单，模板题啦~，因为只需要记录素数的个数，所以连素数数组也没必要开啦

代码实现

#include<bits/stdc++.h>
using namespace std;
const int N=1e8+6;
bool st[N];
int n,k;
int main()
{
	cin>>n;
	for(int i=2;i<=n;i++)
	{
		if(!st[i])
		{
			k++;
			for(int j=i;j<=n;j+=i)
			st[j]=true;
		}
	}
	cout<<k<<endl;
	return 0;
}

(3).最大质因数

杭电-最大质因数位置

题目

解题思路

这道题的关键在于记录最小质因数，只要将每个质数标记为它的最小质因数就好啦~，因为这题范围不算大，所以也很好实现，注意！！存质数时要将素数存入下标，然后记录它的位置，这样下面查找时就可以一下找出来了。

代码实现

#include<stdio.h>
const int N=1e6+6;
int a[N],prime[N],k=1;
int main()
{
	int n;
	a[0]=a[1]=1;
	for(int i=2;i<N;i++)
	{
		if(a[i]==0)
		{
		prime[i]=k++;
		for(int j=i;j<N;j+=i)
		a[j]=i;//将素数的倍数都标记为这个素数，即最小质因数。
		}
	}
	prime[1]=0;
	while(~scanf("%d",&n))
	{
        printf("%d\n",prime[a[n]]);//直接输出就好啦~
	}
	return 0;
} 

(4)Primes Problem

杭电-Primes Problem

题目

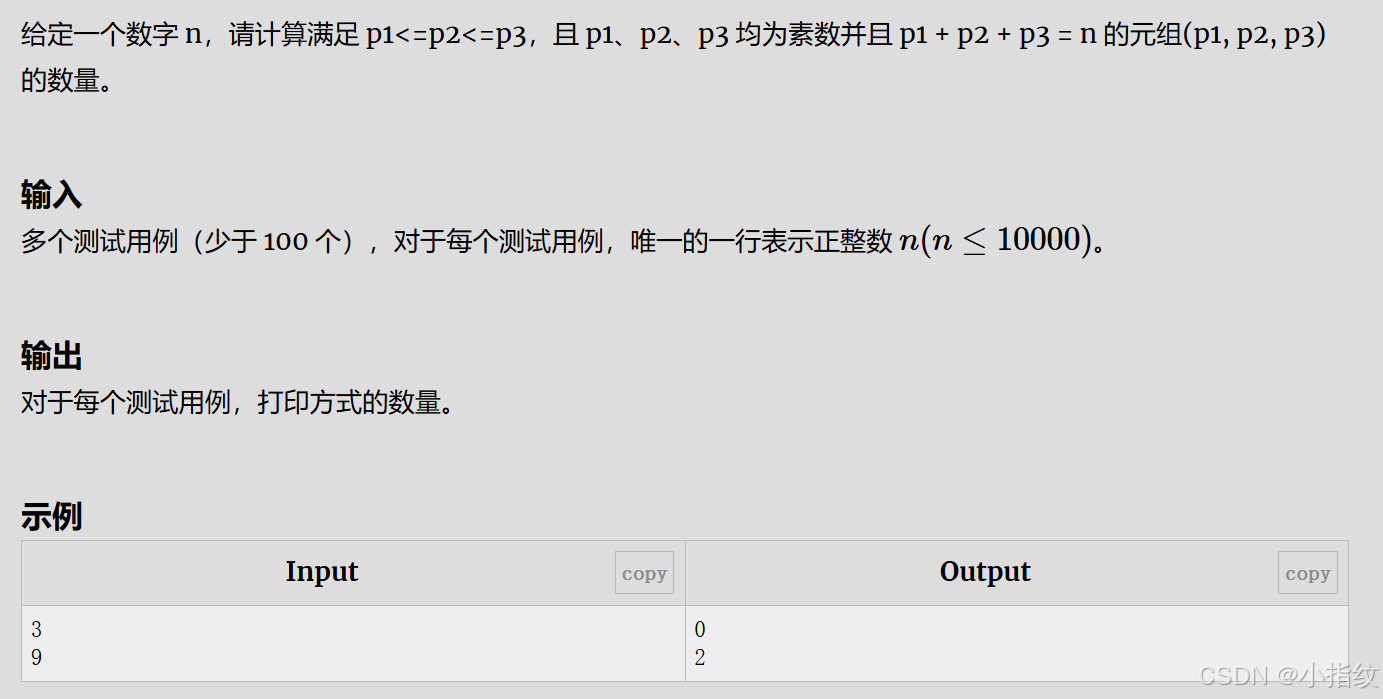
解题思路

因为这道题的范围并不大，可以先将10000以内的质数存入一个质数数组中，然后再去判断符合条件的素数们，这里主要注意一下，如果用三重循环的话时间复杂度过高会超时，所以我们想办法优化一下，找出满足条件的两个质数后，直接判断第三个质数是否满足就好啦~

代码实现

#include<stdio.h>
const int N=1e4+5;
int st[N],primes[N],k,ans,n;
int main()
{
   //存质数
	for(int i=2;i<=10000;i++)
	{
		if(!st[i])
		primes[k++]=i;
		for(int j=0;i*primes[j]<=10000;j++)
		{
			st[primes[j]*i]=true;
			if(i%primes[j]==0)break;
		}
	}
	while(~scanf("%d",&n))
	{
		ans=0;//记得每次初始化
		for(int i=0;;i++)
		{
			if(primes[i]>=n)break;
			for(int j=i;primes[j]<n;j++)
			{
				if(st[n-primes[i]-primes[j]]==0&&n-primes[i]-primes[j]>=primes[j])//优化
				ans++;
			}
		}
		printf("%d\n",ans);
	}

}

好啦~希望你有了上面的基础一定可以自己做一些相关的题目啦！

相关题目练习

1.素数对
2.素数回文

总结

• 小规模数据（n≤1e6）：推荐埃氏筛（实现简单）

• 大规模数据（n≥1e7）：必须使用线性筛

• 需要质因数分解信息：选择带最小质因数记录的线性筛

掌握这三种筛法，可以应对绝大多数需要质数表的算法题目。建议理解原理后熟记线性筛的模板代码,因为它的应用范围最广，大家加油哈~~~！