三维视觉新范式：神经辐射场(Neural Radiance Field)(2)

本文链接：https://blog.csdn.net/2403_85515624/article/details/146186297

3.2.体素网格和MLP混合表达的方法

3.2.1.DVGO

DVGO与前面提到的Plenoxels有相似之处，都使用体素网格来提高重建速度；而不同之处在于Plenoxels的核心目标是通过使用体素网格来完全去除MLP，DVGO的核心目标是通过体素网格与较浅的神经网络的混合方法实现加速。

DVGO通过体素网格与浅神经网络的混合方法加速，这样的设计可以在使用更小的体素网格的情况下，实现相当的或更好的表达效果。本质上，DVGO巧妙地利用了体素网格的存储和高效查询能力，同时借助神经网络的插值能力，取得了良好的效果，能够将 NeRF 一到两天的训练时间减少到半小时以内。

DVGO的两个主要贡献点：

1.在体素密度直接优化中，采用了两个先验算法来避免几何陷入局部最优解，并在五个数据集上表现良好：

一个是低密度初始化（Low-Density Initialization），初始时将所有体素的密度值设置为接近零，通过调整激活函数（如 Softplus）的偏移参数 b，使得初始的体素密度对应的透明度（α值）极低。使用这个先验算法的目的在于：直接优化密度体素网格会导致超快收敛，但容易出现次优解，防止优化过程偏向相机近平面的 “云状” 次优几何解，确保所有采样点在训练初期对相机可见，减少几何偏差。

另一个是给视图计数学习率(View-Count-Based Learning Rate)，较少视图可见的体素一个较低的学习率，可以避免仅为解释少量视图的观察而分配的冗余体素。对每个体素根据其在不同训练视图中的可见次数 $n_{j}$ 调整学习率.

2.提出了后激活体素网格插值，它可以在较低的网格分辨率下实现清晰的边界建模：

之前的工作要么对激活的不透明度进行体素网格插值，要么使用最近邻插值，从而在每个网格单元中产生光滑的表面。从数学和经验上证明，所提出的后激活可以在单个网格单元内建模(超越)尖锐的线性表面。

DVGO的整体流程如图所示

以下是DVGO的表现

效果：

1.收敛速度比使用NVIDIA RTX 2080 Ti GPU的机器上的nerf减少训练时间(从10 - 20小时到15分钟)快了大约两个数量级。
2.以45倍的渲染速度实现了与NeRF相当的视觉质量
3.不需要跨场景的预训练
4.网格分辨率大约是1603，而之前的工作中的网格分辨率在5123到13003之间，以达到与nerf相当的质量

参考文献

DVGO：SUN C, SUN M, CHEN H. Direct voxel grid optimization: Super-fast convergence for radiance fields recon struction[C]//CVPR. [S.l.: s.n.], 2022.

Homepage:GitHub - sunset1995/DirectVoxGO: Direct voxel grid optimization for fast radiance field reconstruction.

3.2.1.2.DVGO的framework

让我们再回到这张图中

DVGO 将整个场景表示为两个 voxel grid，并且使用的依然是 NeRF 中的体渲染，对于从像素上发射的射线上的每一个点，首先在这两个 voxel grid 上进行三线性插值，分别得到这个点的密度特征和颜色特征，再通过各自的解码过程最终得到该点的颜色和密度。这样就把整个场景表示在 voxel grid 和对应的解码器里。

在训练的时候，DVGO 采用了 coarse to fine 的训练方式。在 coarse 阶段，使用先验信息(priors)和多视角图像(training views)训练两个粗粒度的voxel，然后使用其中的密度场确定场景中的空白区域（free space）。在 fine 阶段，利用 coarse 阶段确定的密度场可以得到更紧密的 bbox(tight bbox)，可以将 grid 定义在这个 bbox 内，减少无关变量的训练。并且在体渲染的时候还可以通过粗的密度场提前得知射线上哪些点应当被跳过（空白点和被遮住的那些点）。

从中我们可以得出DVGO快的原因：

1.通过 coarse to fine 的方式跳过了大量无关点的采样。(其中常用的方法有空白空间跳过ESS方法，早期射线终止ERT方法)

2.整个场景的信息主要存储在两个 voxel grid 中，相比于 NeRF，一个空间点的信息直接使用三线性插值就能得到，而不用过一个MLP。

3.2.1.3.原文中的Preliminaries(前言)环节

前言环节对于回顾NeRF还是有一定帮助。

首先 NeRF 将场景用 MLP 表示，使用坐标x推测出密度σ和中间特征，然后用这个中间特征e和视角d推测出这个点的颜色c。

然后用体渲染的方式得到像素点的值

其中， $\alpha _{i}$ 是光线在第 i 个点终止的概率； $T_{i}$ 是从近平面到第 i 个点的累积透射率； $\delta _{i}$ 是到相邻采样点的距离， $c_{bg}$ 是预先定义的背景颜色。

给定已知姿态的训练图像，NeRF 模型通过最小化观测像素颜色C(r)与渲染颜色 $c\hat{}(r)$ 之间的光度均方误差（MSE）进行训练：

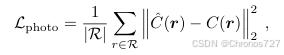
其中，R表示采样小批量中的光线集合。

3.2.1.4.Post-activated density voxel grid(后激活密度体素网格)

这里想要探讨的问题是如何从 density grid 中得到一个点的密度信息。

首先，density grid 上面定义了场景的密度信息，但不需要直接是真实的密度值。具体来说每个 voxel 上的值是一个实数，由于密度是非负的，我们最后需要先将这个实数映射为一个大于零的数才能将输出与真实密度值建立关系。然后用每个点的密度值计算每个点的α(光线终止的概率)。

渲染时需要对一个点做三步操作：插值，激活，求α。

1.插值：因为网格是稀疏的，而我们做体渲染的时候需要的是空间中任意点的信息，所以最简单直接的方式就是用空间点附近的 voxel 进行插值。

2.激活：这里采用的是Mip-NeRF中的 shifted softplus，

其中， $\sigma \ddot{}$ 是 density grid 上的值，取值范围是 R(实数)。

注意，这里不使用常用的relu函数是因为如果一个密度为正的地方的 $\sigma \ddot{}$
如果是负值会导致其经过 relu 之后是0，没有梯度能更新这个值让它能移动到正的部分。

3.求α：求 α 是 NeRF 中计算一个点的瞬时击中率的操作。

这三个操作的顺序是可以交换的，并且作者发现不同的顺序得到的结果还有所差异。

作者证明，后激活能够用更少的网格单元生成尖锐的表面(决策边界)，并且在二维图像上证明了后激活的优越性。

后激活能够表示出更 sharp 的边缘，对应在 NeRF 中就是更sharp的几何。

更详细的证明内容请参阅原文。

3.2.1.5. Fast and direct voxel grid optimization(快速直接的体素网格优化)

上一节是关于DVGO的场景表达，大体上就是体素网格+后激活。这一节要讲的是 3.2.1.2中的 coarse to fine 的训练方式。

通常情况下，场景由空闲空间(即未占用空间)主导。基于此，我们的目标是高效地找到感兴趣的粗三维区域，然后重构需要更多计算资源的精细细节和视图依赖效果。这样可以大大减少后期精细阶段每条射线上查询的点的数量。这就是coarse to fine做的事。

不论是 coarse 还是 fine 阶段，我们都需要知道应该在场景的什么位置创建 grid。作者采用的方式是找一个 BBox 将所有的摄像机截锥包起来，

对应代码：

def _compute_bbox_by_cam_frustrm_bounded(cfg, HW, Ks, poses, i_train, near, far):
    xyz_min = torch.Tensor([np.inf, np.inf, np.inf])
    xyz_max = -xyz_min
    for (H, W), K, c2w in zip(HW[i_train], Ks[i_train], poses[i_train]):
        rays_o, rays_d, viewdirs = dvgo.get_rays_of_a_view(
                H=H, W=W, K=K, c2w=c2w,
                ndc=cfg.data.ndc, inverse_y=cfg.data.inverse_y,
                flip_x=cfg.data.flip_x, flip_y=cfg.data.flip_y)
        if cfg.data.ndc:
            pts_nf = torch.stack([rays_o+rays_d*near, rays_o+rays_d*far])
        else:
            pts_nf = torch.stack([rays_o+viewdirs*near, rays_o+viewdirs*far])
        xyz_min = torch.minimum(xyz_min, pts_nf.amin((0,1,2)))
        xyz_max = torch.maximum(xyz_max, pts_nf.amax((0,1,2)))
    return xyz_min,xyz_max

代码逻辑是，首先拿到训练集中所有的相机位置和视角，然后在生成射线，根据 near 和 far 确定射线上的采样点来均匀采样，把所有这些采样点放一块，求所有这些点的 x,y,z 的最值。通过这样可以保证 grid 能够包含所有要采样的点，并且不会包含过多的无关位置。

3.2.1.6.Coarse geometry searching(粗略几何搜索)

coarse 阶段的主要目的是搞清楚场景的大致几何是什么样子的，所以作者采用了更粗粒度的 grid 和视角无关的颜色，为视图相关颜色开发一个详尽的策略并不在它的主要范围内，它这里只对颜色使用混合表示（具有浅 MLP 的特征网格）。本节的内容则是对3.2.1.2中的两个先验算法的更详细的说明。

1. low-density initialization：

作者发现，在训练开始时，远离相机的点的重要性由于累积的透过率项而降低。因此，粗密度体素网格可能会意外地被困在一个次优的“cloudy”几何，它在相机附近的平面密度更高。导致这个问题的原因如果初始化做的不好，那么后面的采样点都被前面的遮住了，后面的采样点的被击中的概率 $T_{i}$ 就很低，那么这些位置就不会被训练到，网络就一直在纠结是不是前面那些点的颜色或者密度调的不够好，殊不知是重心在射线的后面。

再回到这三个公式

由于 σ 和 δ 都是正的，所以 α 和T都是 0~1 之间的。想要 𝑇尽可能大，就是让 𝛼 尽可能小，𝛿一般是指定好固定的，那就要求 𝜎尽可能的小。所以初始化的时候我们应当让 𝜎接近 0。

那我们就直接让 𝜎¨ 的值初始化为 0。但是这样还不能保证满足 𝑇要求，因为从 𝜎¨到 𝜎还需要经过一个激活函数，故还需要找到一个合适的参数b才行。

实际上，我们只需要让最后一个点的概率 𝑇𝑁尽可能接近 1 就行了，因为随着射线的传播，𝑇是会逐渐减小的，保证射线上概率最低的那个点的概率就能保证整体的概率符合要求。我们把 𝑇𝑁展开：

所以只需要让

其中，一般给 $\alpha ^{(init)}$ 一个很小的初值，代码中的值一般为 $10^{-6}$ (coarse)和 $10^{-2}$ (fine)。

self.alpha_init = alpha_init
self.register_buffer('act_shift', torch.FloatTensor([np.log(1/(1-alpha_init) - 1)]))

2.view-count-based learning rate：

grid 中的不同 voxel 在训练集中的可见性是不同的，有一些 voxel 在大部分训练集视角下都可见，而有一些只在少部分视角下可见。作者认为，可见度不同的 voxel 上的特征应该具有不同的学习率，可见性好的学习率更大，否则设置更小的学习率。(这种动态调整learning rate的方法在深度学习中也很常见)

def voxel_count_views(self, rays_o_tr, rays_d_tr, imsz, near, far, stepsize, downrate=1, irregular_shape=False):
        print('dvgo: voxel_count_views start')
        far = 1e9  # the given far can be too small while rays stop when hitting scene bbox
        eps_time = time.time()
        N_samples = int(np.linalg.norm(np.array(self.world_size.cpu())+1) / stepsize) + 1
        rng = torch.arange(N_samples)[None].float()
        count = torch.zeros_like(self.density.get_dense_grid())
        device = rng.device
        for rays_o_, rays_d_ in zip(rays_o_tr.split(imsz), rays_d_tr.split(imsz)):
            ones = grid.DenseGrid(1, self.world_size, self.xyz_min, self.xyz_max)
            if irregular_shape:
                rays_o_ = rays_o_.split(10000)
                rays_d_ = rays_d_.split(10000)
            else:
                rays_o_ = rays_o_[::downrate, ::downrate].to(device).flatten(0,-2).split(10000)
                rays_d_ = rays_d_[::downrate, ::downrate].to(device).flatten(0,-2).split(10000)

            for rays_o, rays_d in zip(rays_o_, rays_d_):
                vec = torch.where(rays_d==0, torch.full_like(rays_d, 1e-6), rays_d)
                rate_a = (self.xyz_max - rays_o) / vec
                rate_b = (self.xyz_min - rays_o) / vec
                t_min = torch.minimum(rate_a, rate_b).amax(-1).clamp(min=near, max=far)
                t_max = torch.maximum(rate_a, rate_b).amin(-1).clamp(min=near, max=far)
                step = stepsize * self.voxel_size * rng
                interpx = (t_min[...,None] + step/rays_d.norm(dim=-1,keepdim=True))
                rays_pts = rays_o[...,None,:] + rays_d[...,None,:] * interpx[...,None]
                ones(rays_pts).sum().backward()
            with torch.no_grad():
                count += (ones.grid.grad > 1)

作者首先构造了一个 grid 对象 ones，它是作者创建的一个类，这个类的作用就是构造可以训练的 voxel grid，并且可以完成插值等操作。然后在训练集视角上获取射线并在射线上采样点 rays_pts。对 rays_pts 中的每个点，找到它在 ones 中的插值结果，对应的语句是 ones(rays_pts)。然后将这些点的插值结果加起来：ones(rays_pts).sum()。可想而知，到目前为止，只有 rays_pts 中的那些点所在的 voxel 参与了加法，这个时候我们对加法结果进行法向传播：ones(rays_pts).sum().backward()，参与插值的那些 voxel 的梯度会是正的，我们找到这些梯度为正的 voxel：ones.grid.grad > 1，就可以确定哪些 voxel 是可见的。count 是和 grid 同纬度的 tensor，ones.grid.grad > 1 得到的是一个 bool tensor，其中为 True 的那些就是可见 voxel，两个加起来就能实现统计的目的。

3.2.1.7.Fine detail reconstruction(精细细节重建)

fine 阶段采用了更密集的网格，并且使用显隐混合的表达方式（explicit-implicit hybrid representation），其实就是用一个 MLP 当解码器接在颜色网格后面，增强网络对颜色的表达能力。fine 阶段查询一个空间点的颜色和密度的方式改为：

在获取粗糙几何体素网格后，便可启动训练精细几何体素网格。精细体素网格的初始大小设定方法与粗糙体素网格相似，随着训练深度的增加，体素网格大小会进行调整。

同时在精细几何体素网格上并行训练一个特征体素网格，其分辨率始终与精细几何体素网格保持一致，该特征体素网格用于预测空间点的颜色值，因此其生成密度与颜色的公式与粗糙体素网格有所不同。由于精细几何体素网格承担生成最终场景数据的任务，因此引入MLP，利用它的强大插值能力实现更精细的插值效果(DVGO使用的MLP较浅，带来的计算量不大)。在采样方面，由于空间内的占据情况已由粗糙网格得出，故可用ESS，ERT等方法执行射线的空白区域跳过和早期终止等策略。

Known free space and unknown space
这里说明了怎么定义 free space 和 unknown space，方式就是手动设置一个阈值，之下的就是 free space。
Fine voxels allocation
coarse 阶段确定 grid 范围的方式是找到一个包含所有采样点的 BBox。但是有些地方是空的，所以我们可以更具 coarse 阶段得到的 density grid 确定 fine 阶段 grid 所在的区域，将有限的 voxel 尽可能地安排在有密度的地方。
Progressive scaling
受到 NSVF 的启发，作者也是逐渐减小 voxel 的大小。随着训练不断的倍增 grid 的密度，直到最后达到指定数量的 voxel 停止倍增。
Fine-stage points sampling
在 NeRF 中，一个场景的 near-bound 和 far-bound 是定好的一个大致的范围，但是由于我们这里明确知道场景就在空间的一个 grid 内，所以更好的方式是将 near-bound 和 far-bound 设置为每条射线进入 grid 和离开 grid 的点。
Free space skipping
意思是通过 coarse 阶段已经知道场景中哪些位置是空的了，那就不需要在这些位置采样点浪费时间了。
Training objective for fine representation
使用与粗阶段相同的训练损失，但使用更小的权值作为正则化损失，因为作者发现，根据经验，它会带来略好的质量。

3.2.1.8.Loss Function(损失函数)

Loss Function包含三个部分：来自NeRF的 MSE loss 以及两个从 DVGO 中借鉴的 loss。

第一个损失项的作用是使得建模出来的辐射场在训练集视角上渲染要和原图尽可能一致。权重为 1。

第二个损失项的意思是从一个像素中发射的射线上的所有像素点都应该和该像素尽可能接近，这个约束能够帮助网络一开始不要陷入 local minima，使得优化过程更加稳定。但是这个约束并不是符合实际的，因为一条射线上的点的颜色常常是不同的，所以作者给了一个很小的系数 α=0.1（coarse）和 α=0.01（coarse）。

第三个损失项中的 $T_{N+1}$ 表示射线击中背景的概率，它的作用是让一个像素点要么为背景颜色，要么没有背景颜色，尽量避免是二者的混合。