2D Gaussian Splatting for Geometrically Accurate Radiance Fields(用于实现几何精确辐射场的二维高斯溅射)

Chronos727

于 2025-03-24 22:38:38 发布

阅读量973

点赞数 19

分类专栏： 3DGS内容文章标签：计算机视觉人工智能 pytorch

本文链接：https://blog.csdn.net/2403_85515624/article/details/146404893

版权

3DGS内容专栏收录该内容

7 篇文章

订阅专栏

前情提要

各位看官老爷们大家好！大家点个赞吧，这对我真的重要！今天为大家带来2DGS的读书笔记。

三维高斯溅射（3DGS）最近在辐射场重建领域掀起了一场革命，实现了高质量的新视角合成和快速渲染。具体详情可以参阅我的一篇3DGS技术的读书笔记三维高斯溅射(3D Gaussian Splatting,3DGS)-CSDN博客

然而，由于三维高斯在多视角下的不一致性，3DGS 无法精确表示物体表面。作者提出了二维高斯溅射（2DGS），这是一种从多视图图像中对几何精确的辐射场进行建模和重建的全新方法。它的核心思想是将三维空间压缩为一组具有方向的二维平面高斯圆盘。与三维高斯不同，二维高斯在对表面进行固有建模的同时，能够提供视角一致的几何信息。为了精确恢复薄表面并实现稳定的优化，引入了一种利用光线 - 溅射相交和光栅化的透视精确二维溅射过程(a perspective-accurate 2D splatting process uti- lizing ray-splat intersection and rasterization)。此外，还加入了深度畸变和法线一致性项，进一步提高重建质量。实验证明，作者的可微渲染器能够在保持有竞争力的外观质量、快速训练速度和实时渲染能力的同时，实现无噪声且细节丰富的几何重建。(从论文的实验来看，2DGS的视觉效果好不少，但是数值效果跟3DGS差不多)

这里再贴一段原文的开头，来更具体地理解2DGS技术：

Fig. 1. Our method, 2DGS, (a) optimizes a set of 2D oriented disks to represent and reconstruct a complex real-world scene from multi-view RGB images. These optimized 2D disks are tightly aligned to the surfaces. (b) With 2D Gaussian splatting, we allow real-time rendering of high quality novel view images with view consistent normals and depth maps. (c) Finally, our method provides detailed and noise-free triangle mesh reconstruction from the optimized 2D disks.

从中不难得到一些关于2DGS的关键信息：

2DGS方法先优化了一组带有方向的二维圆盘，以便从多视角的 RGB 图像中表示和重建一个复杂的真实世界场景，而经过优化的二维圆盘与物体表面紧密贴合。

借助二维高斯溅射技术，能够实时渲染出高质量的新视角图像，且这些图像的法线和深度图在视角上是一致的。

根据经过优化的二维圆盘，重建出细节丰富且无噪点的三角形网格。

原文地址：https://arxiv.org/pdf/2403.17888

项目地址：https://github.com/hbb1/2d-gaussian-splatting

1.Introduction

由于用于对完整角辐射进行建模的三维体高斯与表面的薄型特性存在冲突，3DGS在捕捉复杂几何形状方面仍存在不足。另一方面，早期的研究表明，表面元素（surfels，即 surface elements 的缩写）是一种表示复杂几何形状的有效方式。表面元素通过形状和阴影属性对物体表面进行局部近似，并且可以从已知的几何形状中推导得出。

它们作为一种高效的几何表示方式，在同步定位与地图构建（SLAM）以及其他机器人任务中得到了广泛应用。随后的进展，将表面元素纳入了可微框架。然而，这些方法通常需要真实（GT）几何形状、深度传感器数据，或者在已知光照的受限场景下才能运行。

1.1.2DGS方法简介

受上面这些研究工作的启发，作者提出了用于三维场景重建和新视角合成的二维高斯溅射法，该方法结合了两者的优势，同时克服了它们的局限性。与三维高斯溅射法（3DGS）不同，作者的方法使用二维高斯基元来表示三维场景，每个基元定义一个具有方向的椭圆盘。二维高斯相对于三维高斯的显著优势在于其在渲染过程中能够精确表示几何形状。具体而言，3DGS 在像素光线与三维高斯的交点处评估高斯值，这导致从不同视点渲染时深度不一致。相比之下，作者的方法采用显式的光线 - 溅射相交计算，实现了透视正确的溅射效果，如下图所示，进而显著提高了重建质量。此外，二维高斯基元中固有的表面法线使得可以通过法线约束直接对表面进行正则化处理。与基于表面元素（surfels）的模型不同，作者的二维高斯可以通过基于梯度的优化从未知几何形状中恢复出来。

但由于三维重建任务本质上具有无约束性，仅使用光度损失进行优化会导致重建结果出现噪声。为了增强重建效果并获得更平滑的表面，作者还引入了两个正则化项：深度畸变和法线一致性。深度畸变项将沿光线分布的二维基元集中在一个紧密的范围内，解决了渲染过程中忽略高斯之间距离的局限性。法线一致性项最小化渲染法线图与渲染深度梯度之间的差异，确保由深度和法线定义的几何形状保持一致。

此处为三维高斯溅射法（3DGS）和二维高斯溅射法（2DGS）的对比。3DGS 从不同视点进行值评估时，会使用不同的相交平面，从而导致结果不一致。而2DGS则能提供多视点一致的值评估。

1.2.总结

作者提出了一种高效的可微二维高斯渲染器，通过利用二维表面建模、光线 - 溅射相交和体积积分，实现了透视正确的溅射效果。
引入了两种正则化损失，以改进表面重建并实现无噪声的重建结果。
与其他显式表示方法相比，作者的方法在几何重建和新视角合成（NVS）方面取得了最先进的成果。

2. Related Work

Novel view synthesis(NVS，新视角合成)，3D reconstruction(三维重建)，Differentiable Point-based Graphics(可微的基于点的图形学)，3DGS等在这里不作过多赘述。我们主要来关注两个与2DGS同期的工作-SuGaR，NeuSG和2DGS的区别。当然还要来关注我们的主角-2DGS。

2.1.与近期工作的区别

与 SuGaR 用 3D 高斯近似 2D 高斯不同，2DGS方法直接使用 2D 高斯，简化了过程，并在无需额外网格细化的情况下提升了最终的几何效果。

NeuSG 联合优化 3D 高斯基元和隐式有符号距离函数（SDF）网络，并从 SDF 网络中提取表面，而我们的方法利用 2D 高斯基元进行表面近似，提供了一种更快且概念上更简单的解决方案。

2.2.2D Gaussian Splating

为了在保持高质量的新视图合成的同时精确地重建几何形状，我们提出了可微的二维高斯溅射（2DGS）。下图能让您更加生动地理解2DGS：

二维高斯溅射体是椭圆形圆盘，其特征由一个中心点pk、切向向量tu和tv，以及两个控制方差的缩放因子（su和sv）来描述。它们的椭圆投影通过光线与溅射体的交点采样，并在图像空间中通过alpha-blending(阿尔法混合,控制像素的透明度)进行累加。二维高斯溅射（2DGS）通过梯度下降法来重建诸如颜色、深度和法线等表面属性。

2.2.1.Modeling

三维高斯溅射是在一个团块中对整个角辐射进行建模，而2DGS通过采用嵌入三维空间的 “扁平” 二维高斯来简化三维建模过程。使用二维高斯建模时，基元将密度分布在一个平面圆盘内，把法线定义为密度变化最剧烈的方向。这一特性使得它能更好地与薄表面对齐。

且不需要密集的点云或真实的法线作为输入，仅依靠稀疏的校准点云和光度监督就能同时重建外观和几何形状。

让我们再回到这张图中，2DGS的基元法线由两个正交的切向量tw=tu×tv定义，且可以将方向排列成一个3×3的旋转矩阵R=[tu,tv,tw]，并将缩放因子排列成一个3×3的对角矩阵S，其最后一个元素为零。这步操作可以将三维空间中的物体方向调整后投影到二维平面。因此，二维高斯函数是在世界空间中的一个局部切平面内定义的，该切平面是经过参数化的：

其中H是一个4×4的齐次变换矩阵，用于表示二维高斯的几何形状。对于uv空间中的点u=(u,v)，其二维高斯值随后可以通过标准高斯函数来计算：

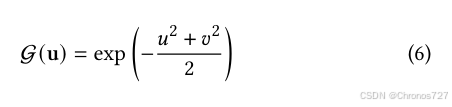
中心点pk、缩放因子(su,sv) 以及旋转参数(tu,tv) 均为可学习参数。每个二维高斯基元都具有不透明度α，以及依赖于视角的外观属性c，该外观属性是通过球谐函数进行参数化的。

2.2.2.Splatting

渲染二维高斯图形的一种常见策略是使用affine approximation of the perspective projection(透视投影的仿射近似法 )，将二维高斯基元投影到图像空间上。然而，这种投影仅在高斯图形的中心位置是准确的，并且随着与中心距离的增加，近似误差也会增大。为了解决这个问题，Zwicker 等人提出了一种基于齐次坐标的公式。具体来说，将二维溅射体投影到图像平面上，可以用齐次坐标中的一般二维到二维映射来描述。设W是一个4×4的组合变换矩阵，用于表示从世界空间到屏幕空间的变换。因此，屏幕空间中的点可通过以下方式获得：

其中x表示从相机发出的一条齐次光线，该光线穿过像素点(x,y)，并在深度z处与溅射体相交。为了对二维高斯图形进行光栅化处理，Zwicker 等人提出使用一种隐式方法将其圆锥曲线投影到屏幕空间中。然而，这种逆变换会引入数值不稳定性，尤其是当溅射体退化为一条线段时（也就是说，当从侧面观察它时）。为了解决这个问题，先前的表面溅射渲染方法会使用一个预定义的阈值来舍弃这种病态变换。然而，这样的方案在可微渲染框架中带来了挑战，因为设置阈值可能会导致优化过程不稳定。为了解决这个问题，我们采用了一种受 Sigg 等人启发的显式光线与溅射体相交的方法。(铺垫结束，全体起立！)

2.2.2.1.Ray-splat Intersection(光线与溅射体的相交)

通过找到三个不平行平面的交点来高效地确定光线与溅射体的交点，这是一种最初为专用硬件设计的方法。给定一个图像坐标x=(x,y)，将投影空间中一个像素的光线参数化为两个正交平面的交线：x平面和y平面。具体来说，x平面由法向量(−1,0,0)和偏移量x定义。x平面可以表示为一个四维齐次平面hx=(−1,0,0,x)T(此处的T为矩阵的转置)。类似地，y平面是hy=(0,−1,0,y)T(此处的T为矩阵的转置)。因此，光线x=(x,y)由这两个平面的交线确定。

接下来，再将这两个平面都转换为二维高斯基元的局部坐标，即uv坐标系。请注意，使用变换矩阵M来变换平面上的点，等同于使用逆转置矩阵 $M^{-T}$ 来变换齐次平面参数。因此，应用M= $(WH)^{-1}$ 等同于应用 $(WH)^{T}$ ，这样就无需进行显式的矩阵求逆运算，从而得到。

二维高斯平面上的点表示为(u,v,1,1)。同时，交点应该落在变换后的x平面和y平面上。因此有：

这就得到了一种求交点u(x)的高效方法：

其中 $h_{u}^{i}$ 、 $h_{v}^{i}$ 是四维平面的第i个参数。根据公式 (5)，请注意 $h_{u}^{3}$ 和 $h_{v}^{3}$ 始终为零。一旦我们得到了局部坐标(u,v)，我们就可以使用公式 (7) 计算交点的深度z，并使用公式 (6) 计算高斯值。

2.2.2.2.Degenerate Solutions(部分退化解)

当从倾斜的视角观察一个二维高斯图形时，它在屏幕空间中会退化为一条直线。因此，在光栅化过程中它可能会被遗漏。为了处理这些情况并使优化过程更加稳定，作者采用了the object-space low-pass filter(Botsch等人提出的物体空间低通滤波器)。

其中u(x)由公式 (10) 给出，c是中心点pk的投影。直观地说，G^(x)由一个固定的屏幕空间高斯低通滤波器确定下限，该滤波器的中心为c，半径为σ。在作者的实验中，将σ设置为22，以确保在渲染过程中使用了足够多的像素。

2.2.2.3.Rasterization(光栅化)

2DGS这里采用与3DGS相似的光栅化方法，首先，为每个高斯基元计算一个屏幕空间边界框。然后，根据二维高斯图形中心点的深度对它们进行排序，并依据其边界框将它们组织成图块。最后，使用volumetric alpha blending(体素α混合)从前到后融合alpha-weighted(α加权)的外观属性：(从这里我们也可以看出，原始3DGS的光栅化方法是一个非常适合CUDA的，出色的方法)

当累积的不透明度达到饱和时，迭代过程就会终止。

3.Training

二维高斯方法虽然在几何建模方面很有效，但如果仅通过光度损失进行优化，可能会导致重建结果出现噪声，这是三维重建任务中固有的一个挑战。为了缓解这一问题并改善几何重建效果，我们引入了两个正则化项：深度畸变和法线一致性。

3.1.Depth Distortion(深度畸变)

与神经辐射场（NeRF）不同，三维高斯溅射（3DGS）的体渲染不考虑相交的高斯基元之间的距离。因此，高斯分布的扩散可能会导致相似的颜色和深度渲染效果。这与表面渲染不同，在表面渲染中，光线与第一个可见表面恰好相交一次。为了缓解这个问题，我们从 Mip-NeRF360 中获得灵感，并提出了一种深度畸变损失，通过最小化光线与溅射体交点之间的距离，使权重分布集中在光线上：

其中，

是第i个交点的混合权重，zi是交点的深度。与 Mip-NeRF360 中的畸变损失不同，在 Mip-NeRF360 中zi是采样点之间的距离且不进行优化，我们的方法通过调整交点深度zi直接促使溅射体的分布更加集中。请注意，我们以与sun等人类似的方式使用 CUDA 高效地实现了这个正则化项。

3.2.Normal Consistency(法线一致性)

由于2DGS的表示方法是基于二维高斯表面元素的，所以必须确保所有的二维溅射体在局部都与实际表面对齐。在体渲染的情境中，沿着光线可能存在多个半透明的面元，作者将实际表面视为在交点ps的中点处，此时累积的不透明度达到0.5。然后，按如下方式使溅射体的法线与深度图的梯度对齐：

其中，i表示沿光线方向与溅射体相交的索引，ω表示交点的混合权重，ni表示溅射体朝向相机方向的法线，N是由深度图的梯度估计出的法线。具体而言，N是通过对附近深度点采用有限差分法计算得出的，如下所示：

通过使溅射体的法线与估计出的表面法线对齐，能确保二维溅射体能够在局部近似实际的物体表面。

3.3.Final Loss

最后，利用一组带有姿态信息的图像，从初始的稀疏点云开始对作者的模型进行优化。最小化以下损失函数：

其中Lc是一个 RGB 重建损失，它结合了 L1 损失以及D-SSIM(差异结构相似性)项，而Ld和Ln是正则化项。对于有边界的场景，将α设置为 1000；对于无边界的场景，将α设置为 100；并且对于所有场景，β都设置为 0.05。

4.Experiments

这个环节展示对二维高斯溅射重建方法的评估，包括与先前最先进的隐式和显式方法在外观和几何方面的比较。然后，分析所提出的各个组件的作用。

4.1.Implementation

作者在三维高斯溅射（3DGS）的框架基础上，使用自定义的 CUDA 内核实现了二维高斯溅射方法。作者扩展了渲染器，以输出用于正则化的深度畸变图、深度图和法线图。在训练过程中，作者按照 3DGS 中的自适应控制策略增加二维高斯基元的数量。由于作者的方法并不直接依赖于投影后的二维中心的梯度，因此将三维中心pk的梯度投影到屏幕空间作为一种近似。同样地，作者采用 0.0002 的梯度阈值，并每 3000 步去除不透明度低于 0.05 的溅射体。在单块 GTX RTX3090 GPU 上进行所有实验。

4.1.1.Mesh Extraction

为了从重建的二维溅射体中提取网格，作者利用投射到像素上的溅射体的深度值来渲染训练视图的深度图，并使用 Open3D 采用截断有符号距离融合（TSDF）方法来融合重建的深度图。在 TSDF 融合过程中，我们将体素大小设置为 0.004，截断阈值设置为 0.02。作者还扩展了原始的三维高斯溅射（3DGS）方法，使其能够渲染深度图，并采用相同的表面重建技术，以便进行公平的比较。

以下是比较结果的展示：