马走日（骑士巡游）问题（递归，DFS，回溯）

本文链接：https://blog.csdn.net/2403_89586338/article/details/145618742

1.思路

本题运用到了递归，深度优先，回溯算法。以(0,0)为中心建立直角坐标系，假设从（0，0）开始，由于走位为日字形，每一个象限都有两个方向，共八个方向。第一象限可以走到（1，2）和（2，1），同理，将八个方向储存至列表中dir=[(2,1),(1,2), (-2,1),(-1,2), (-2,-1),(-1,-2), (2,-1),(1,-2)]，如图所示：

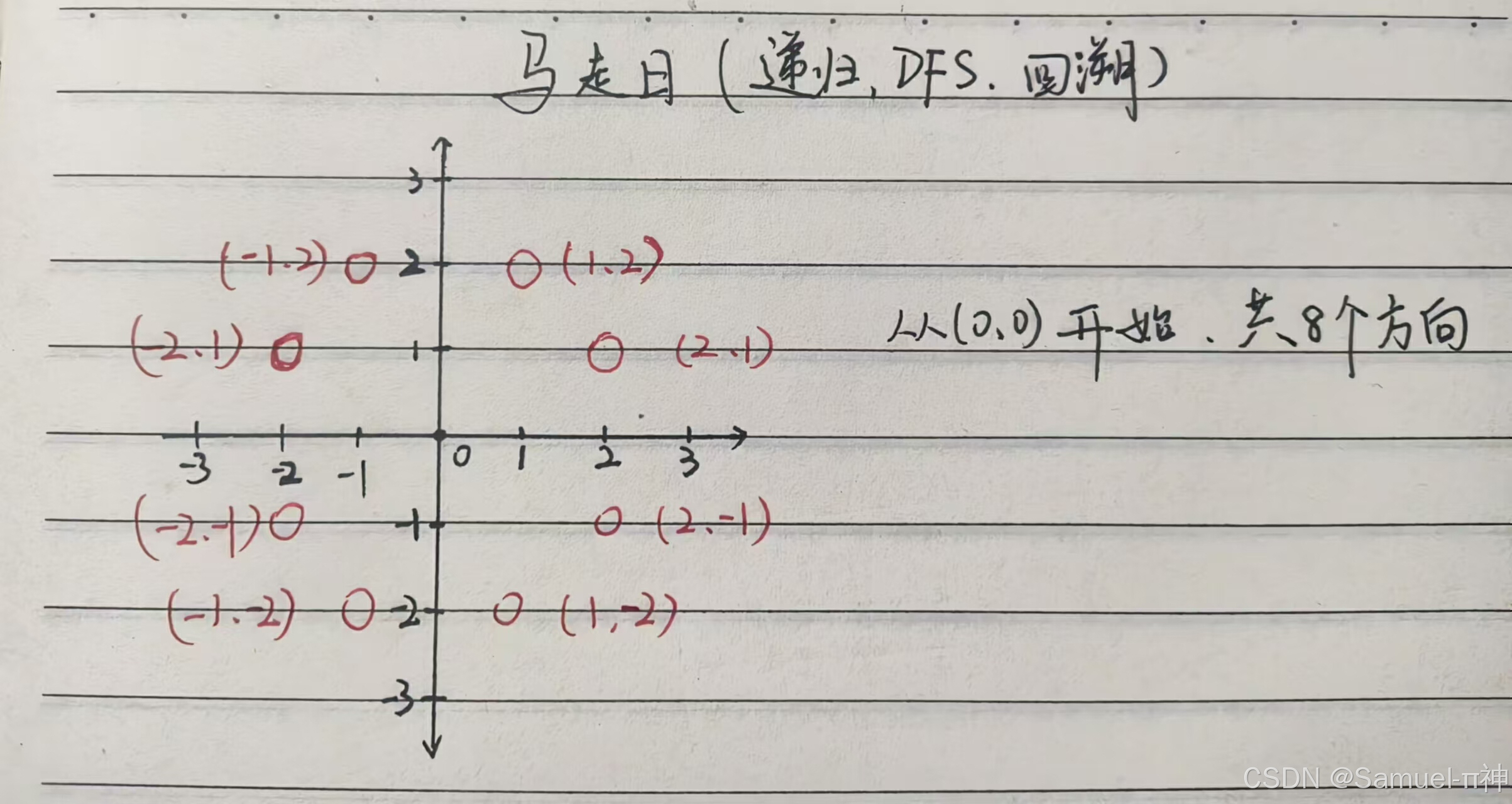
定义一个函数move(s,y,step)，用step来记录走过的步数，每一次递归会使步数加1，当step=n*m=棋盘总格数时，就表示已经遍历过一遍棋盘。再用num路径数，然后进行八个方向的写法，for循环遍历列表，将列表中第i个元组的第1个元素赋值给x，将列表中第i个元组的第2个元素赋值给y，当x与y没有过界时，且当前位置为0时，就把当前位置改为1，重新递归后step+1，然后进行回溯操作，依次重置棋盘每一个位置为0，以便进行其他方向的操作。

2.逐步编写程序

2.1 初始化部分

m, n = 3, 4
dir = [( 2,  1), ( 1,  2),  (-2, 1), (-1, 2), 
       (-2, -1), (-1, -2),  (2, -1), (1, -2)]
board = [[0] * n for i in range(m)]
# 运用列表推导式，输出一个m行n列的棋盘
num = 0

# m 和 n：分别表示棋盘的行数和列数，这里是一个 3 行 4 列的棋盘。
# dir：存储骑士的 8 种可能移动方向，每个元素是一个二元组 (dx, dy)，
# 表示在 x 方向和 y 方向上的偏移量。
# board：一个二维列表，用于表示棋盘，初始时所有格子的值都为 0，表示未被访问。
# num：全局变量，用于记录骑士巡游的路径数量，初始值为 0。

2.2 递归函数 `move`

def move(x, y, step):
    global num
    if step == n * m:
        num += 1
        return
    for i in range(8):
        nx = x + dir[i][0]
        ny = y + dir[i][1]
        if nx >= 0 and nx < m and ny >= 0 and ny < n and board[nx][ny] == 0:
            # 判断坐标没有出界，且此处值为1
            board[nx][ny] = 1
            move(nx, ny, step + 1)
            board[nx][ny] = 0

# 参数解释：
# x 和 y：当前骑士所在的格子的坐标。
# step：当前已经走过的步数。

# 递归终止条件：
# 1.当 step 等于 n * m 时，说明骑士已经遍历了棋盘上的所有格子，路径数量 num 加 1，然后返回。
# 2.当for循环遍历完8个方向，没有找到合适的位置时，返回

# 递归过程：
# 遍历骑士的 8 种可能移动方向，计算新的坐标 (nx, ny)。
# 检查新的坐标是否在棋盘范围内，并且该格子未被访问（board[nx][ny] == 0）。
# 如果满足条件，将该格子标记为已访问（board[nx][ny] = 1），
# 然后递归调用 move 函数，继续探索下一个格子，步数加 1。

# 回溯操作：在递归调用返回后，将该格子标记为未访问（board[nx][ny] = 0），以便尝试其他可能的路径。

2.3 程序调用

x, y = 0, 0
board[x][y] = 1
move(x, y, 1)
print(num)

# 初始化骑士的起始位置为 (0, 0)，并将该格子标记为已访问。
# 调用 move 函数开始探索骑士巡游路径，初始步数为 1。
# 最后打印出所有可能的巡游路径数量。

2.4 完整程序

sum=int(input())
for a in range(sum):
    m,n,x,y=map(int,input().split())

    dir=[(2,1),(1,2),  (-2,1),(-1,2),  (-2,-1),(-1,-2),  (2,-1),(1,-2)]
    board=[[0]*n for i in range(m)]
    num=0

    def move(x,y,step):
        global num
        if step==n*m:
            num+=1
            return
        for i in range(8):
            nx=x+dir[i][0]
            ny=y+dir[i][1]
            if nx>=0 and nx<m and ny>=0 and ny<n and board[nx][ny]==0:
                board[nx][ny]=1
                move(nx,ny,step+1)
                board[nx][ny]=0

    board[x][y]=1
    move(x,y,1)
    print(num)

3.递归，回溯解释说明

def move(x, y, step):
    global num
    if step == n * m:
        num += 1
        return
    for i in range(8):
        nx = x + dir[i][0]
        ny = y + dir[i][1]
        if nx >= 0 and nx < m and ny >= 0 and ny < n and board[nx][ny] == 0:
            board[nx][ny] = 1
            move(nx, ny, step + 1)
            board[nx][ny] = 0

# 1. 递归调用 move(nx, ny, step + 1)
# 在 move(x, y, step) 函数中，当找到一个满足条件（新位置 (nx, ny) 在棋盘范围内且未被访问）
# 的移动
# 方向时，会将该位置标记为已访问（board[nx][ny] = 1），然后递归调用 move(nx, ny, step + 1) 
# 继续探索新位置的后续路径。

# 2. move(nx, ny, step + 1) 内部的探索过程在 move(nx, ny, step + 1) 函数内部，
#同样会有一个 for # 循环来遍历骑士从 (nx, ny) 位置出发的 8 种可能移动方向：

for i in range(8):
    new_nx = nx + dir[i][0]
    new_ny = ny + dir[i][1]
    if new_nx >= 0 and new_nx < m and new_ny >= 0 and new_ny < n 
        and board[new_nx][new_ny] == 0:
        board[new_nx][new_ny] = 1
        move(new_nx, new_ny, step + 2)
        board[new_nx][new_ny] = 0
# 这个 for 循环会尝试骑士从 (nx, ny) 出发的每一个可能移动方向。如果某个方向的新位置满足条件，
# 就会继续递归调用 move 函数进行更深层次的探索。

# 3.遍历完所有可能移动方向
# 当 move(nx, ny, step + 1)中的for 循环遍历完所有 8 种移动方向后，意味着从 (nx, ny) 位置出发
# 的所有可能路径都已经被尝试过了，并且没有找到有效的路径（即没有满足 step == n * m 这个终止条件
# 的路径）。此时， for 循环结束，move(nx, ny, step + 1) 函数的执行也就结束了。

# 4.返回上一层递归调用
# 由于函数执行结束，程序会自动返回到调用move(nx, ny, step + 1)的地方，也就是move(x, y, step)
# 函数中的move(nx, ny, step + 1)这一行之后。接着会执行board[nx][ny] = 0进行回溯操作，
# 将(nx, ny)位置标记为未访问，以便尝试从(x, y)位置出发的其他移动方向。

回溯操作：

回溯操作是在递归调用返回的过程中逐步进行的，每次递归调用返回时只处理当前探索的那个格子。因为递归是一层一层深入和返回的，每次返回上一层时，只需要恢复当前这一步所做的状态改变。

例如，骑士从位置 A 移动到位置 B，再从位置 B 移动到位置 C，当从位置 C 出发的所有路径探索完后，先将位置 C 对应的 board 元素恢复为 0，然后回到位置 B 继续探索其他可能路径；当位置 B 的所有路径都探索完后，再将位置 B 对应的 board 元素恢复为 0，以此类推。

如图所示：

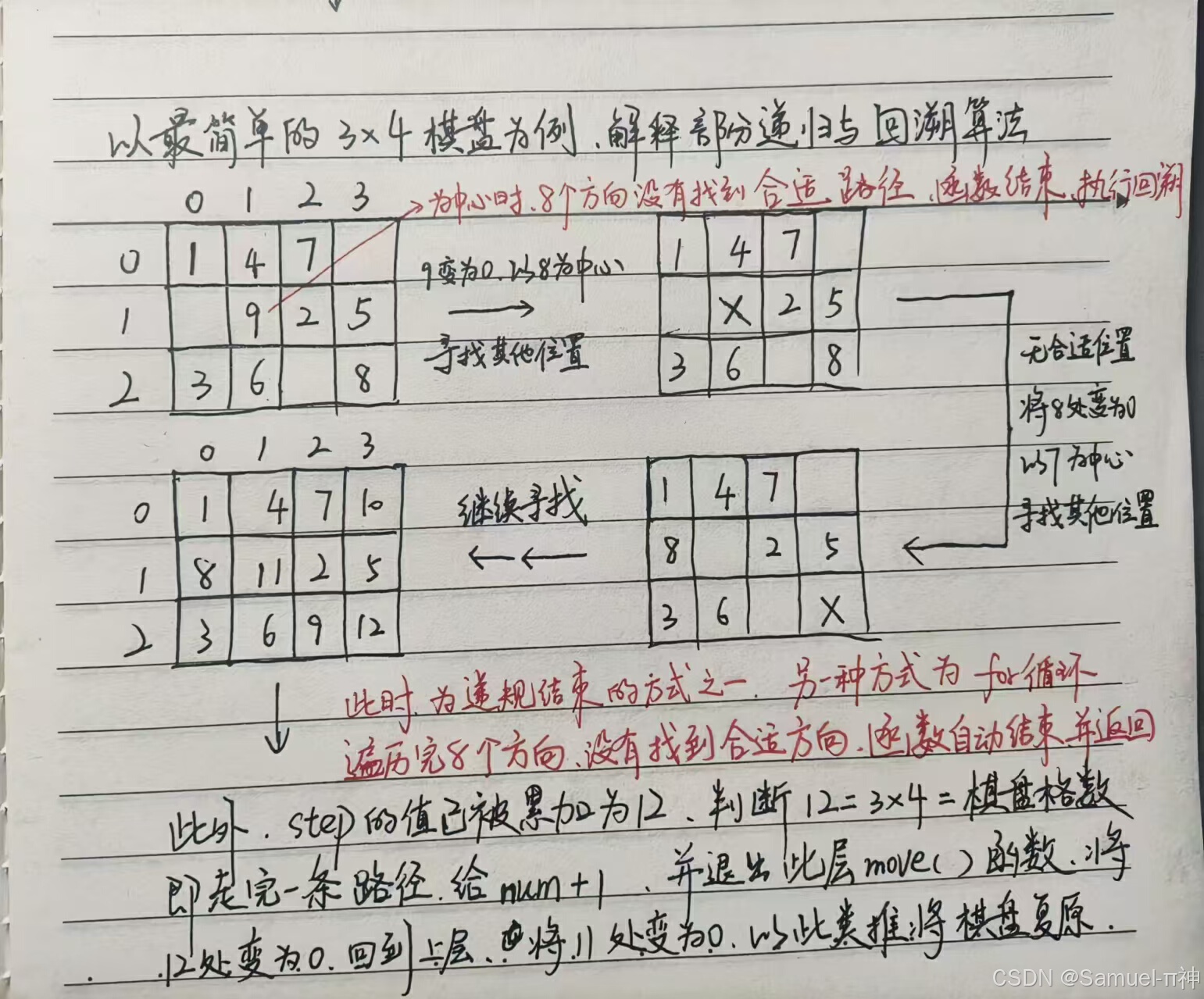
回溯操作的时机：

回溯操作在递归调用返回时进行。具体来说，当程序从一个递归层级返回上一个递归层级时，就会执行回溯操作。在代码中，move(nx, ny, step + 1) 调用返回后，紧接着就执行 board[nx][ny] = 0 进行回溯。

例如，假设骑士从位置 (x, y) 移动到了 (nx, ny)，并从 (nx, ny) 开始继续探索。当从 (nx, ny) 出发的所有可能路径都被探索完后，程序会回到 (x, y) 这一层级，此时就会将 (nx, ny) 标记为未访问，以便尝试从 (x, y) 出发的其他移动方向。

综上所述，回溯操作通过恢复棋盘格子的访问状态，使得程序能够在搜索过程中撤销之前的选择，尝试其他可能的路径，从而找出所有可能的骑士巡游路径。

4.运行过程：

为了详细看出程序如何运行，可以在move函数中输出坐标与步数，并在得到结果时用短横线标记

m,n=3,4
dir=[(2,1),(1,2),  (-2,1),(-1,2),  (-2,-1),(-1,-2),  (2,-1),(1,-2)]
board=[[0]*n for i in range(m)]
num=0
def move(x,y,step):
    global num
    print(x,y,step)

    if step==n*m:
        num+=1
        print("-"*20)

        return
    for i in range(8):
        nx=x+dir[i][0]
        ny=y+dir[i][1]
        if nx>=0 and nx<m and ny>=0 and ny<n and board[nx][ny]==0:
            board[nx][ny]=1
            move(nx,ny,step+1)
            board[nx][ny]=0
x,y=0,0
board[x][y]=1
move(x,y,1)
print(num)

输出：
0 0 1
2 1 2
0 2 3
2 3 4
1 1 5
0 3 6
2 2 7
0 1 8
1 3 9
2 0 9
1 2 10
1 0 8
1 0 4
2 2 5
0 3 6
1 1 7
2 3 8
0 1 6
1 3 7
2 0 7
1 2 8
1 3 3
0 1 4
2 2 5
0 3 6
1 1 7
2 3 8
0 2 9
1 0 10
1 0 6
0 2 7
2 3 8
1 1 9
0 3 10
2 0 5
1 2 6
1 2 2
2 0 3
0 1 4
2 2 5
0 3 6
1 1 7
2 3 8
0 2 9
2 1 10
1 3 11
1 0 10
1 0 6
0 2 7
2 3 8
1 1 9
0 3 10
2 1 8
1 3 9
1 3 5
2 1 6
0 2 7
2 3 8
1 1 9
0 3 10
2 2 11
1 0 12
--------------------
1 0 8
2 2 9
0 3 10
1 1 11
2 3 12
--------------------
2