全套大气层内航天器飞行动力学matlab仿真模型 该MATLAB仿真模型涉及到航天器在地球大气层内的运动规律、控制策略以及飞行性能分析。

于 2025-04-23 08:25:39 发布
阅读量612 收藏 23
点赞数 20
文章标签： matlab 算法 开发语言
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/2501_90824910/article/details/147439407
版权

全套大气层内航天器飞行动力学matlab仿真模型
该MATLAB仿真模型涉及到航天器在地球大气层内的运动规律、控制策略以及飞行性能分析。
在MATLAB环境中，构建了大气层内航天器的六自由度模型，即考虑航天器在三维空间中的位置（x, y, z）和姿态（俯仰、偏航、滚转）的变化。这些动态方程通常基于牛顿第二定律和欧拉运动方程建立，结合大气阻力、重力、地球自转等多种因素的影响。 通过定义大气层的物理参数，如密度、压强、温度等，利用这些参数计算航天器受到的气动载荷，包括阻力和升力。
对于复杂形状的航天器，可能需要进行气动特性预估或通过风洞实验获取数据。
本模型考虑地球引力场的影响。地球引力模型可以简化为球谐函数，或者采用更精确的高阶模型，如EGM96或GGM05C。通过这些模型，可以计算出航天器在不同高度处的引力分量。 在确定了所有外力后，我们构建了动力学方程，并将其转化为状态空间形式。涉及微分方程组的求解，我们利用MATLAB的ode45等内置求解器进行处理。
同时，我们还定义了初始条件，比如初始位置、速度和姿态角。 在仿真过程中，加入控制器设计，如PID控制器或滑模控制，以确保航天器按照预定轨迹飞行或执行特定任务。这些控制律通过线性化或非线性优化方法来设计，并集成到仿真模型中。
此外，MATLAB的Simulink环境提供了图形化建模工具，可以直观地搭建系统模型并进行实时仿真。通过Simulink，我们方便地实现硬件在环测试，验证控制系统的性能。
仿真结果的分析和可视化也是必不可少的。本MATLAB模型提供了丰富的数据分析工具和图形绘制功能，可以用于评估飞行轨迹、速度、加速度等关键指标，以及控制系统的效果。
大气层内航天器飞行动力学MATLAB仿真模型是一个综合性的工程问题，涵盖了流体力学、航天器动力学、控制理论等多个领域的知识。通过修改本M文件代码可以构建精确的仿真模型，对航天器的飞行性能进行深入研究和优化。
在这里插入图片描述

文章目录


构建一个完整的大气层内航天器飞行动力学MATLAB仿真模型是一个复杂的任务，涉及到多个学科的知识。以下是一个简化版的MATLAB代码示例，用于模拟大气层内航天器的六自由度运动。这个代码包括了基本的动力学方程、地球引力模型、气动载荷计算和PID控制器设计。 

% 六自由度航天器飞行动力学仿真模型

clc;
clear;

% 常量定义
Re = 6371e3; % 地球半径 (m)
g0 = 9.81;   % 标准重力加速度 (m/s^2)
rho0 = 1.225; % 海平面空气密度 (kg/m^3)
H_scale = 8500; % 大气标高 (m)

% 初始条件
x0 = [0; 0; 100e3]; % 初始位置 (m) [x, y, z]
v0 = [7000; 0; 0];  % 初始速度 (m/s) [vx, vy, vz]
q0 = [1; 0; 0; 0];  % 四元数初始姿态 [qw, qx, qy, qz]
w0 = [0; 0; 0];     % 初始角速度 (rad/s) [wx, wy, wz]

state0 = [x0; v0; q0; w0];

% 时间设置
tspan = [0 1000]; % 仿真时间 (s)

% 调用ODE求解器
[t, state] = ode45(@(t, state) dynamics(t, state), tspan, state0);

% 动力学方程
function dstate = dynamics(~, state)
    x = state(1:3);   % 位置
    v = state(4:6);   % 速度
    q = state(7:10);  % 四元数
    w = state(11:13); % 角速度
    
    % 计算高度
    r = norm(x);
    h = r - Re;
    
    % 大气密度模型
    rho = rho0 * exp(-h / H_scale);
    
    % 气动力计算 (简单模型)
    Cd = 0.5; % 阻力系数
    A = 10;   % 参考面积 (m^2)
    D = 0.5 * rho * norm(v)^2 * Cd * A; % 阻力
    L = 0;    % 升力 (假设为零)
    
    % 引力计算
    g = -(g0 * (Re / r)^2) * x / r; % 简化的引力模型
    
    % 总外力
    F_total = g - D * v / norm(v);
    
    % 控制输入 (PID控制器)
    u = pid_controller(state);
    
    % 平移动力学
    dv = F_total / m + u(1:3);
    
    % 旋转动力学
    Ixx = 1000; Iyy = 2000; Izz = 3000; % 惯性矩 (kg*m^2)
    I = diag([Ixx, Iyy, Izz]);
    dw = inv(I) * (u(4:6) - cross(w, I * w));
    
    % 四元数更新
    dq = 0.5 * quat_multiply(q, [0; w]);
    
    % 状态导数
    dstate = [v; dv; dq; dw];
end

% PID控制器
function u = pid_controller(state)
    % 示例：简单的比例控制
    Kp = 1e-3; % 比例增益
    Ki = 0;    % 积分增益
    Kd = 0;    % 微分增益
    
    error = [0; 0; 0]; % 假设目标误差为零
    u = Kp * error;    % 控制输入
end

% 四元数乘法
function q_out = quat_multiply(q1, q2)
    qw1 = q1(1); qx1 = q1(2); qy1 = q1(3); qz1 = q1(4);
    qw2 = q2(1); qx2 = q2(2); qy2 = q2(3); qz2 = q2(4);
    
    q_out = [
        qw1*qw2 - qx1*qx2 - qy1*qy2 - qz1*qz2;
        qw1*qx2 + qx1*qw2 + qy1*qz2 - qz1*qy2;
        qw1*qy2 - qx1*qz2 + qy1*qw2 + qz1*qx2;
        qw1*qz2 + qx1*qy2 - qy1*qx2 + qz1*qw2
    ];
end

% 结果可视化
figure;
plot3(state(:,1), state(:,2), state(:,3));
xlabel('X (m)');
ylabel('Y (m)');
zlabel('Z (m)');
title('航天器轨迹');
grid on;

说明：

  1. 动力学模型：包含平移和旋转动力学。
  2. 气动力模型：使用简单的阻力公式，升力设为零。
  3. 引力模型：简化为球形引力场。
  4. 控制器：实现了一个简单的PID控制器（仅比例控制）。
  5. 四元数：用于描述航天器的姿态变化。

你可以根据实际需求扩展该模型，例如引入更精确的气动模型、复杂控制器或地球引力场模型。
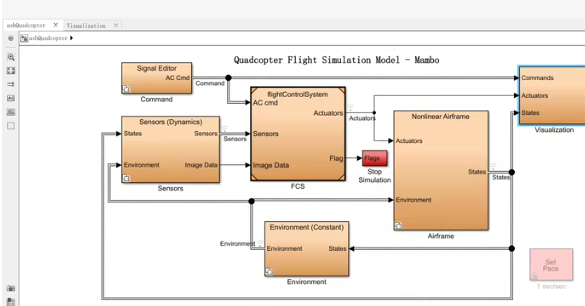
在这里插入图片描述
（Quadcopter）飞行仿真模型。这个模型包含了信号编辑器、传感器、环境、飞行控制系统（FCS）、非线性机身模型以及可视化模块等部分。下面是一个简化的MATLAB Simulink代码示例，用于模拟四旋翼飞行器的基本飞行动态。

Simulink Model Setup

首先，你需要在MATLAB中打开Simulink并创建一个新的模型文件。然后，你可以根据以下步骤和代码片段来构建你的四旋翼飞行器仿真模型。

1. 创建基本模型结构

在Simulink中，你可以通过拖拽不同的模块来构建你的模型。这里我们提供一个简化版的四旋翼飞行器模型的Simulink脚本，你可以将其保存为.m文件并在MATLAB中运行以生成Simulink模型。

% 创建一个新的Simulink模型
modelName = 'QuadcopterFlightSimulation';
new_system(modelName);
open_system(modelName);

% 添加必要的模块
add_block('simulink/Sources/Constant', [modelName '/Command']);
add_block('simulink/Sources/Signal Editor', [modelName '/Signal Editor']);
add_block('simulink/Ports & Subsystems/Inport', [modelName '/Commands']);
add_block('simulink/Ports & Subsystems/Outport', [modelName '/Actuators']);
add_block('simulink/Ports & Subsystems/Outport', [modelName '/States']);
add_block('simulink/Ports & Subsystems/Outport', [modelName '/Visualization']);

% 添加子系统
add_block('simulink/Ports & Subsystems/Subsystem', [modelName '/AC cmd']);
add_block('simulink/Ports & Subsystems/Subsystem', [modelName '/RightControlSystem']);
add_block('simulink/Ports & Subsystems/Subsystem', [modelName '/Nonlinear Airframe']);
add_block('simulink/Ports & Subsystems/Subsystem', [modelName '/Sensors (Dynamics)']);
add_block('simulink/Ports & Subsystems/Subsystem', [modelName '/Environment (Constant)']);

% 设置连接线
add_line(modelName, 'Command/1', 'AC cmd/1');
add_line(modelName, 'Signal Editor/1', 'AC cmd/2');
add_line(modelName, 'AC cmd/1', 'RightControlSystem/1');
add_line(modelName, 'RightControlSystem/1', 'Nonlinear Airframe/1');
add_line(modelName, 'Nonlinear Airframe/1', 'Actuators/1');
add_line(modelName, 'Nonlinear Airframe/2', 'States/1');
add_line(modelName, 'Nonlinear Airframe/3', 'Visualization/1');

% 打开模型查看
open_system(modelName);
2. 定义子系统功能

接下来，你需要定义每个子系统的具体功能。例如，RightControlSystem可以包含PID控制器，Nonlinear Airframe可以包含四旋翼的动力学方程等。

RightControlSystem 子系统

在这个子系统中，你可以添加PID控制器来控制四旋翼的姿态和位置。

% 在RightControlSystem子系统中添加PID控制器
open_system([modelName '/RightControlSystem']);
add_block('simulink/Continuous/PID Controller', [modelName '/RightControlSystem/PID']);
set_param([modelName '/RightControlSystem/PID'], 'P', '1', 'I', '0.1', 'D', '0.01');
Nonlinear Airframe 子系统

在这个子系统中，你可以定义四旋翼的动力学方程。

% 在Nonlinear Airframe子系统中添加动力学方程
open_system([modelName '/Nonlinear Airframe']);
add_block('simulink/User-Defined Functions/MATLAB Function', [modelName '/Nonlinear Airframe/Dynamics']);
set_param([modelName '/Nonlinear Airframe/Dynamics'], 'Script', 'function y = fcn(u)');

在MATLAB Function模块中，你可以编写具体的动力学方程代码。

3. 运行仿真

最后，你可以设置仿真参数并运行仿真。

% 设置仿真参数
set_param(modelName, 'StopTime', '100');
set_param(modelName, 'Solver', 'ode45');

% 运行仿真
sim(modelName);

以上代码只是一个基础框架，
在这里插入图片描述
这是一个涉及流体力学、几何建模和优化算法的复杂问题。以下是一个基于MATLAB的简化示例代码，用于模拟和优化飞行器外形参数以减少空气阻力。

1. 定义飞行器外形参数

首先，我们需要定义飞行器的几何参数，并创建一个函数来计算这些参数对应的飞行器外形。

function [x, y] = generate_aircraft_shape(params)
    % params: [L1, L2, R1, R2, d1, d2, t1, t2]
    
    L1 = params(1);
    L2 = params(2);
    R1 = params(3);
    R2 = params(4);
    d1 = params(5);
    d2 = params(6);
    t1 = params(7);
    t2 = params(8);
    
    % Generate points for the aircraft shape
    x = [-L1 -L1+R1 -L1+R1+d1 -L1+R1+d1+L2 -L1+R1+d1+L2+R2 -L1+R1+d1+L2+R2+d2];
    y = [0 R1 R1+t1 R1+t1 R2+t2 R2+t2];
    
    % Add symmetry for the lower part
    x = [x fliplr(x)];
    y = [y fliplr(-y)];
end

2. 计算空气阻力

接下来，我们需要一个函数来计算给定外形下的空气阻力。这里我们使用一个简化的公式来表示阻力与外形的关系。

function drag = calculate_drag(params)
    % Calculate the drag based on the aircraft shape parameters
    
    [x, y] = generate_aircraft_shape(params);
    
    % Simplified drag calculation (example formula)
    drag = sum(abs(diff(y))) * sum(abs(diff(x)));
end

3. 优化算法

我们可以使用MATLAB内置的优化工具箱中的fminsearch函数来寻找最优的飞行器外形参数。

% Initial guess for the parameters
initial_params = [1, 1, 0.5, 0.5, 0.2, 0.2, 0.1, 0.1];

% Perform optimization
optimized_params = fminsearch(@calculate_drag, initial_params);

% Display the optimized parameters
disp('Optimized Parameters:');
disp(optimized_params);

% Plot the optimized aircraft shape
[x_opt, y_opt] = generate_aircraft_shape(optimized_params);
plot(x_opt, y_opt);
axis equal;
title('Optimized Aircraft Shape');
xlabel('X');
ylabel('Y');
grid on;

4. 进一步改进

上述代码只是一个非常基础的示例，实际应用中可能需要考虑更多的因素，例如：

  • 使用更精确的流体动力学模型（如CFD仿真）来计算阻力。
  • 添加更多几何参数以更准确地描述飞行器外形。
  • 考虑材料属性、重量分布等因素对飞行性能的影响。
  • 使用更高级的优化算法（如遗传算法、粒子群优化等）来寻找全局最优解。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值