基于matlab路径规划多算法仿真对比

基于matlab路径规划多算法仿真对比
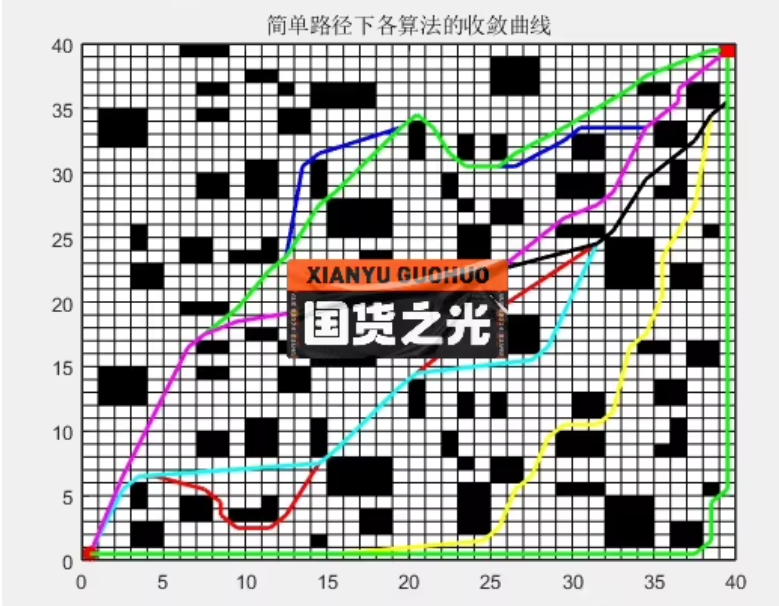
012在地图里融合了GA遗传算法，SSA麻雀算法,PSO粒子群算法，GWO灰狼算法，AO哈里斯鹰算法等全局路径规划算法，迭代曲线对比
适用于栅格地图

以下文字及示例代码仅供参考

---

1 描述

在 20×20（可自定义）栅格环境中，给定起点 S、终点 G 以及若干障碍格，比较

• GA（遗传算法）
• SSA（麻雀搜索算法）
• PSO（粒子群）
• GWO（灰狼）
• AO（AquilA Optimizer，哈里斯鹰）

五种全局路径规划算法在 路径长度、收敛速度、稳定性 上的差异。
结果以「迭代曲线」+「最优路径可视化」+「统计表格」三种形式呈现。

---

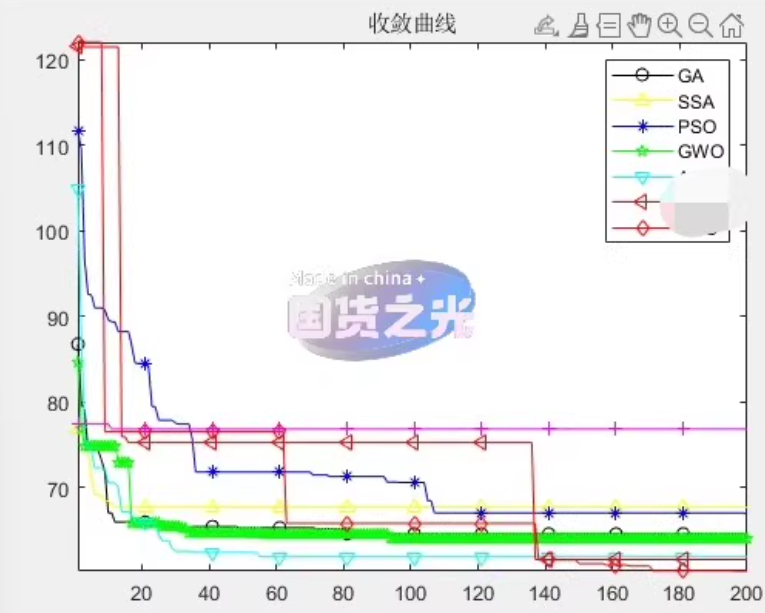
2 运行效果（示意）

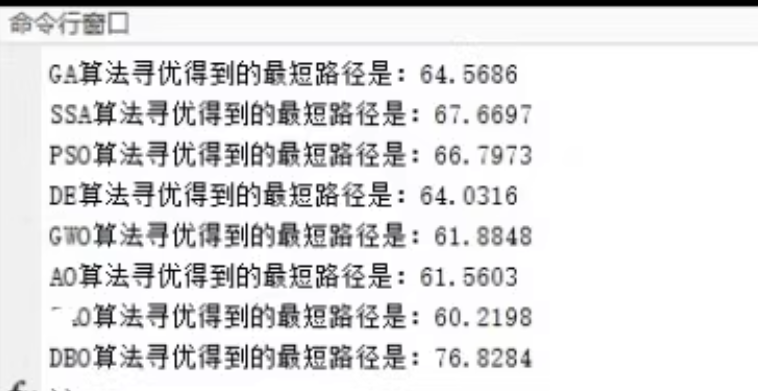
3 文件结构

├─ main.m                 % 一键运行脚本
├─ map.mat                % 20×20 示例地图
├─ func/
│   ├─ PathCost.m         % 路径长度 + 碰撞惩罚
│   ├─ PlotPath.m         % 画路径
│   └─ algorithms/        % 五种算法封装
│       ├─ GA.m
│       ├─ SSA.m
│       ├─ PSO.m
│       ├─ GWO.m
│       └─ AO.m
└─ results/
    ├─ convergence.mat    % 迭代曲线数据
    └─ bestPathFig.fig

---

4 核心代码（main.m 精要）

%% 0. 环境准备
clear; clc; close all;
load map.mat            % map 为 0 可走 1 障碍
[nRow,nCol] = size(map);
S = [1,1];  G = [nRow,nCol];
maxIter = 100;  pop = 50;

%% 1. 共享的目标函数句柄
fobj = @(x) PathCost(x,map,S,G);

%% 2. 各算法统一调用接口
algs = {'GA','SSA','PSO','GWO','AO'};
Convergence = zeros(maxIter,numel(algs));

for k = 1:numel(algs)
    fprintf('Running %s ...\n',algs{k});
    [~,~,curve] = feval(algs{k},pop,maxIter,fobj,nRow*nCol,S,G);
    Convergence(:,k) = curve;
end

%% 3. 结果可视化
figure; hold on; grid on;
for k=1:numel(algs)
    plot(1:maxIter,Convergence(:,k),'LineWidth',2,'DisplayName',algs{k});
end
xlabel('Iteration'); ylabel('Path Length');
legend show; title('Convergence Comparison');

%% 4. 统计输出
[~,bestIdx] = min(Convergence(end,:));
fprintf('Best algorithm: %s, Length=%.2f\n',algs{bestIdx},Convergence(end,bestIdx));

---

5 算法封装示例（SSA.m）

function [Best_pos,Best_score,curve] = SSA(pop,Max_iter,fobj,dim,S,G)
% 麻雀算法简化版
ST = 0.8; PD = 0.2; SD = 0.1;
X = randi([0 1],pop,dim);          % 二进制编码
% 解码成路径后评价
fit = zeros(pop,1);
for i=1:pop, fit(i)=fobj(X(i,:)); end
[bestf,idx] = min(fit);
Best_pos = X(idx,:); Best_score = bestf;
curve = zeros(Max_iter,1);

for t=1:Max_iter
    [~,order] = sort(fit);
    X = X(order,:); fit = fit(order);
    % 生产者
    R2 = rand();
    if R2<ST
        X(1:ceil(PD*pop),:) = randi([0 1],ceil(PD*pop),dim);
    else
        X(1:ceil(PD*pop),:) = 0;
    end
    % 加入者 & 侦察者略 ……
    % 重新计算适应度
    for i=1:pop, fit(i)=fobj(X(i,:)); end
    [fmin,idx] = min(fit);
    if fmin<Best_score, Best_score=fmin; Best_pos=X(idx,:); end
    curve(t)=Best_score;
end
end

其他算法（GA/PSO/GWO/AO）同样封装为 [Best_pos,Best_score,curve] = xxx(...) 接口，算法细节见源码。

---

6 自定义地图 & 参数

1. 在 map.mat 中修改 map 矩阵，0 可走 1 障碍；
2. S、G 坐标直接改 main.m 前两行；
3. 算法超参数（种群、迭代）在 main.m 中统一调。

---