机器学习 性能度量

该文章内容旨在通过机器学习课程进行读书笔记以提高对课程内容的理解。如内容有误，请指正，谢谢！

以下部分图片及文字内容来源于：

《机器学习》（周志华，清华大学出版社）

《机器学习初步（2025春）》、《机器学习进步（2025春）》——学堂在线APP

---

性能度量

性能度量是衡量模型泛化能力的评价标准，匝它反映了任务需求，在对比不同模型的能力时，使用不同的性能度量往往会导致不同的评判结果。

以下是对分类任务中常用的性能度量进行解释。

1.错误率与精度

分类任务中最常见的两种性能度量是错误率和精度。在m个样本中有a个样本分类错误，错误率E＝a/m，1-a/m则称之为精度。

2.查准率、查全率与F1

在遇到更多种任务时，错误率和精度并不能很好地去胜任。比如“所有合格的零件在所有零件里面被挑出来的有多少”，“选出来的零件里面有多少是合格的”。对于二分类问题，可以把样例根据真实情况和学习期预测的类别组合在一起，并将它们划分为四种情形：“真正例（true positive）、假反例（false negative）、假正例（false positive）、真反例（true negative）”。样例总数＝ TP + FN + FP + TN。下表为分类结果的“混淆矩阵”。

查准率=预测和真实相符 / 所有预测为正

查全率=预测和真实相符 / 所有真实为正

 根据学习器的预测结果按照正例可能性大小的顺序对样例进行排序，并诸葛把样本作为正例进行预测，则每次可以计算出当前的查全率和查准率。以查准率作为纵轴，查全率作为横轴，就得到了查准率-查全率曲线，即“P-R曲线”，以下为P-R曲线图示意图。

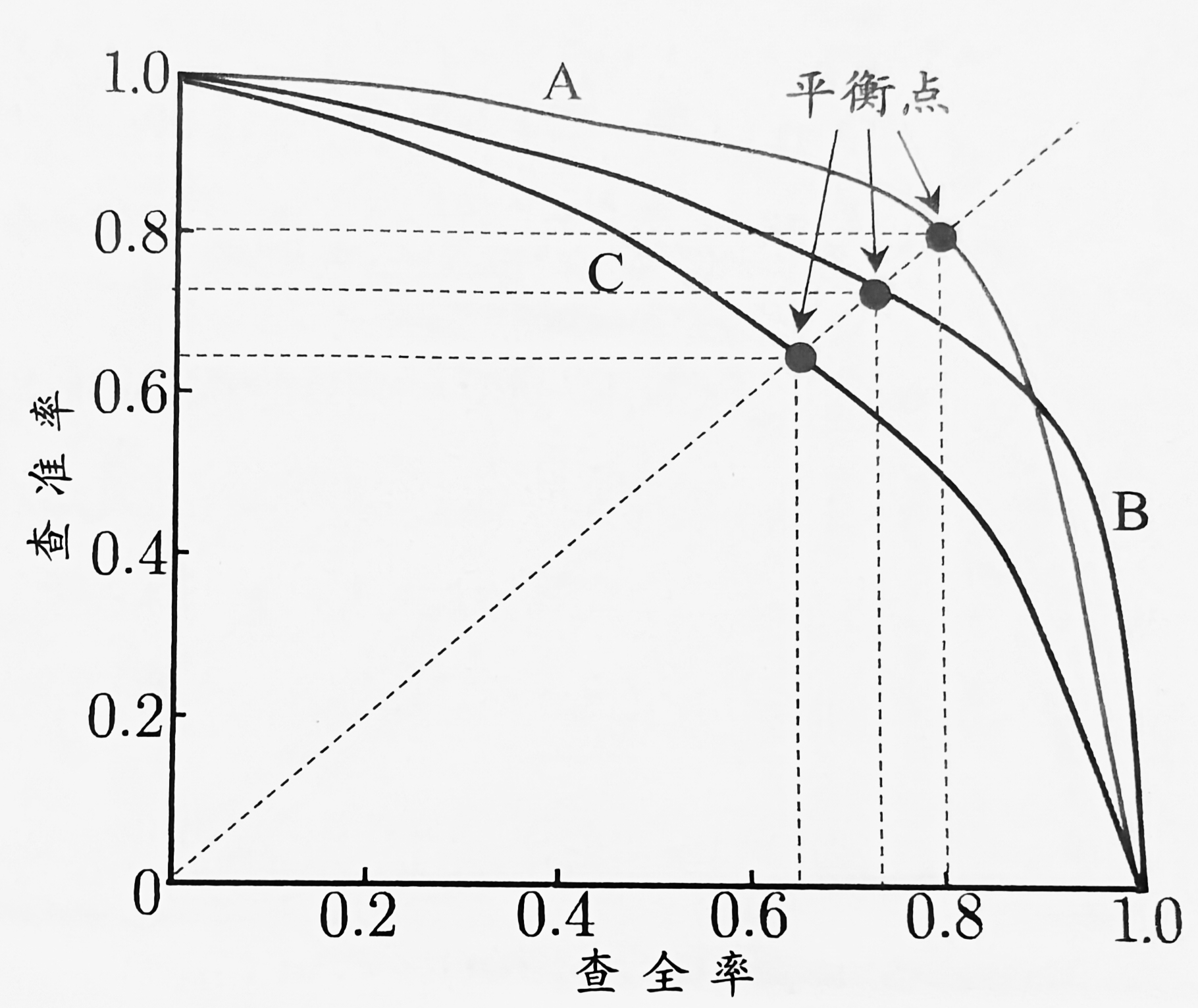
 A、B、C分别对应一种算法。

从上图我们可以得知，学习器A性能优于学习器C，学习器B优于学习器C，但学习器AS和学习器B我们并不能直接判断出谁的性能更好，只能说在某种需求下学习器A的性能优于学习器B，学习器B也有可能在别的情况下性能优于学习器A。

但是，实际上的P-R图并不像图示所给的那么美观那么平滑，图像是有很多折线的。以下借用周老师在《机器学习进步（2025春）》视频里面的例子进行解读。

 

 在上图中，图形的位置越靠近左边代表着算法觉得作为正例的可能性越大，反之可能性越小，但实际上正方形代表真实情况的正例，而三角形代表反例。我们需要根据实际需求在图上进行划分，来得出查准率和查全率的值。划分位置的左右边分别表示预测结果的正反例。

 例如，上图中，我们可以得出预测结果为正例的有2，反例是4，真实情况的正例和反例都是3。预测结果和实际情况相符的，即预测结果和真实情况都是正例的为1。

由此，可以计算出查准率=1/2，查全率=1/3。

再回到P-R图中，当查准率=查全率时的取值，会出现新的度量“平衡点（BEP）”。

相对比较简化的平衡点来说，我们更常用的是F1度量：

F1度量的一般形式：

 当β=1时，则是标准的F1，当β<1时查准率有更大影响，当β>1时查全率有更大影响。

当我们有n个二分类混淆矩阵时，又如何计算出查准率和查全率，以下介绍两种做法。

第一种做法是在每个混淆矩阵上分别计算出P和R，再计算平均值，得到的值称为“宏查准率（macro-P）”、“宏查全率（macro-R）”，接着将得出的平均值代入上面的F1中，我们就得到了“宏F1（macro-F1）”。

另外一种做法时将各个混淆矩阵的对应元素进行平均，得到TP、TN、FP、FN的平均值，再基于这些计算出新的P、R，分别是“微查准率（micro-P）”、“微查全率（micro-R）”，再带入F1当中，得到“微F1（micro-F1）”。