【机器学习】学习笔记2

该文章内容旨在通过机器学习课程进行读书笔记以提高对课程内容的理解。如内容有误，请指正，谢谢！

以下部分图片及文字内容来源于：【(超爽中英!) 2024公认最好的【吴恩达机器学习】教程！附课件代码 Machine Learning Specialization-哔哩哔哩】​​​​​​

《机器学习》（周志华，清华大学出版社）

---

本周学习了［吴恩达机器学习］视频当中关于“线性回归模型”的章节以及《机器学习》（周志华，清华大学出版社）第二章的“经验误差与过拟合”和“评估方法”。

线性回归模型

模型

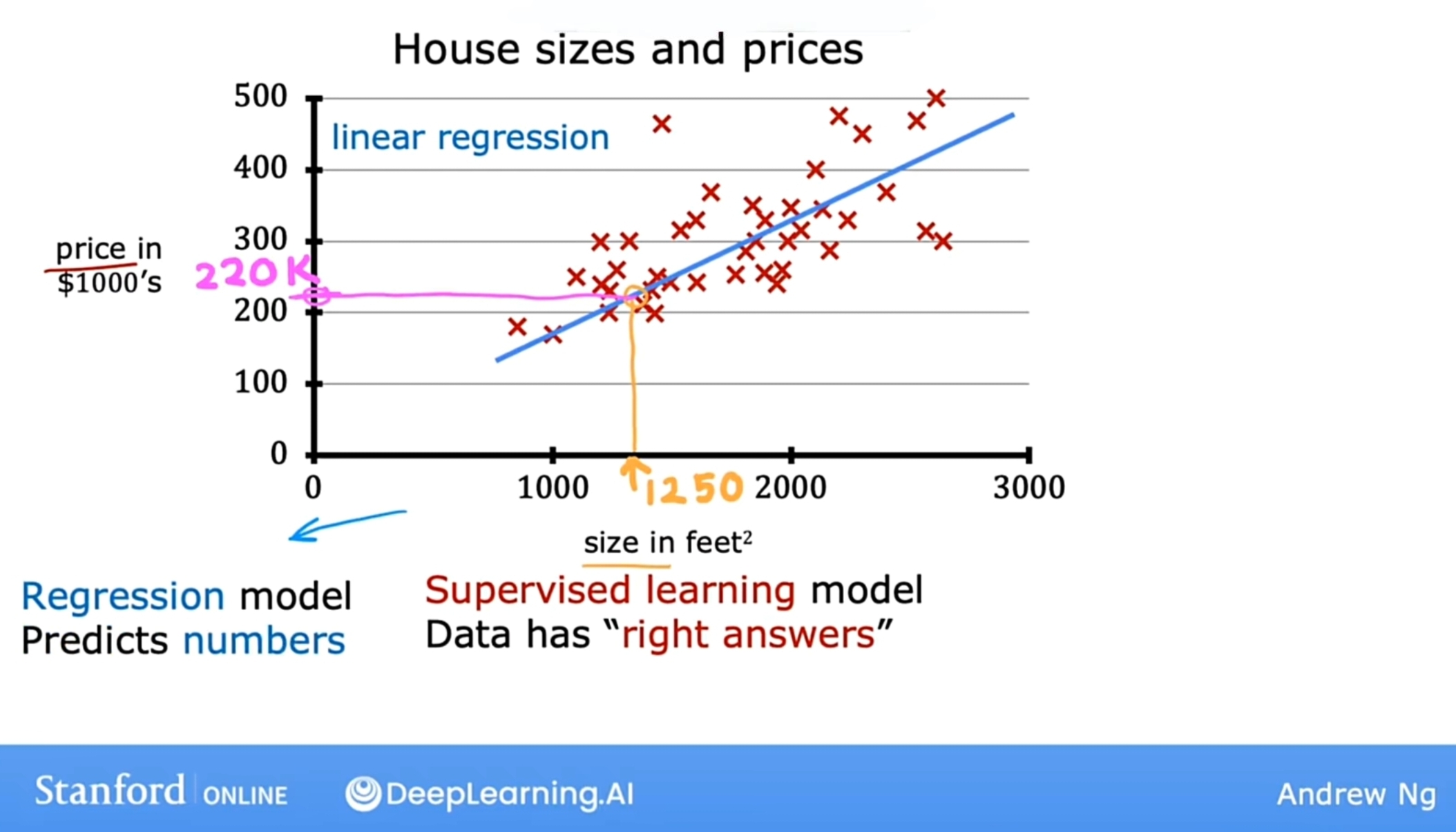
以下是课程的第一个模型，线性回归模型。即把一条直线拟合到数据上。沿用上节课所用的房子面积和价格的数据表，我们基于图中和数据拟合的直线，可以预测出当X＝1250时，对应的Y对应的值大约是220 。线性回归是回归模型当中的一种，也是一种特定的监督学习模型。

训练集

预测房屋价格时，我们首先通过用训练集（如下图）来训练模型，从而让模型能够预测价格。

• x：输入变量
• y：输出变量，目标变量
• m：训练样本总数
• （x，y）：单个训练样本
• （x⁽ⁱ⁾，y⁽ⁱ⁾）：第“ i ”个训练样本

x与y的值是一一对应的。引入i值的目的是给训练集索引，指的是表中的第i行。

监督学习的工作流程

把一个数据集输入到监督学习算法当中，它做了些什么？借由下图理解。

•  f：函数，即模型
• x：输入，输入特征
• y-hat：估计值，预测值
• y：目标，即训练集中的实际真实值

我们再次借由预测房屋价格的例子来进行对工作流程的解释。令x指代房屋尺寸，将x输入到f这一个模型当中，它就会接受输入x并输出一个估计值或预测值y-hat，即对应尺寸的房屋价格。

那我们又应该怎样去表示这个函数f ？

•  w，b：实数
• x：输入，输入特征

上图中，依旧使用一条直线来表示函数f。

基于上图的函数，我们可以用数学知识来理解，的函数一样是在表达x与y的对应关系。只不过这条直线是根据数据集来拟合产生的，作用是辅佐产生预测值。

这种特定的模型就叫线性回归，更具体地说，基于上表叫单变量线性回归。因为我们始终是只有单一的，唯一的输入特征x。

---

经验误差与过拟合

分类错误的样本数占样本总数的比例称为“错误率”，错误率用E＝a/m表示。精度写作（1-a/m）×100% 。实际预测输出与样本的真实输出之间的误差为“误差”。学习器在训练集上的误差称作“训练误差”或者“经验误差”，在新样本上的误差称为“泛化误差”。把训练样本自身的一些特点当做所有潜在样本都会有的一般性质导致的泛化性能下降就叫做“过拟合”。

我更习惯用自己的话来解释这段话并进行理解。把一名学生比作疯狂的学习机器，让他写完一百道题并检验。“错误率”就是他写错的题目占题目总数。“精度”就是他答对的题数占比。“误差”就是他自己预估的成绩和实际成绩的差距。“训练误差”（“经验误差”）指的是他在这一百道题上的误差。重新给他一百道题完成并检验，他在这些新题目里面的误差就是“泛化误差”。至于“过拟合”，意思就是这个学生把刚开始的一百道题练到吐，练到会得不能再会的时候，在面对新的题目的时候他并不能很好地去完成，这就是“过拟合”。