LeetCode 98. 验证二叉搜索树（Validate Binary Search Tree）

98. 验证二叉搜索树

📘题目描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

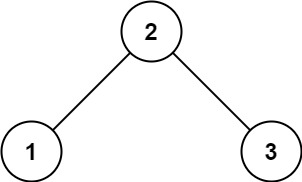
输入：root = [2,1,3]
输出：true

示例 2：

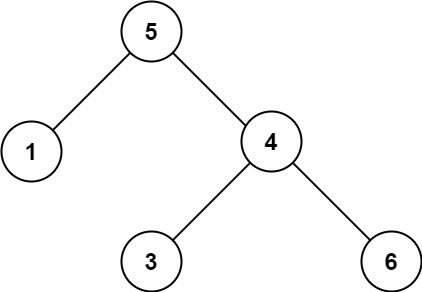
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

💡解题思路：递归 + 上下界约束

🧠核心思想

对每个节点 node：

• 它的值必须满足：left < node.val < right，其中 left 和 right 是从父节点继承而来的合法范围

• 左子树的范围是：(left, node.val)

• 右子树的范围是：(node.val, right)

✅Python 实现 

class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        def helper(node, left, right):
            if not node:
                return True
            if not (left < node.val < right):
                return False
            return helper(node.left, left, node.val) and \
                   helper(node.right, node.val, right)

        return helper(root, float('-inf'), float('inf'))

⏱️复杂度分析 

项目	复杂度	说明
时间复杂度	O(n)	每个节点访问一次
空间复杂度	O(h)	递归栈空间，最坏 O(n)

其中 n 是节点数，h 是树的高度。

📌常见错误点总结 

错误点	正确做法说明
忽略了非直接子节点的约束	不能只比较左节点 < 当前节点 < 右节点
没有传递父节点的范围信息	每一层必须传递上下界
使用中序遍历判断，未记录前一个值	中序法也可做，但需记录 prev 值来比较

🆚拓展：中序遍历法也可判断 BST？

是的！中序遍历二叉搜索树会得到严格递增序列：

class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        self.prev = None
        def inorder(node):
            if not node:
                return True
            if not inorder(node.left):
                return False
            if self.prev is not None and node.val <= self.prev:
                return False
            self.prev = node.val
            return inorder(node.right)
        return inorder(root)

🎯总结

• ✅ 建议掌握两种方式：

  • 递归上下界法（推荐）

  • 中序遍历递增法

• 本题是二叉树中最经典的结构合法性判断题，是 BST 类型题目的基础。