相信大家都有了解过二叉树,那么二叉搜索树又是什么呢?从名字中我们可以看到二叉搜索树和二叉树区别就在于搜索二字,我们可以猜测二叉搜索树相较于普通二叉树而言在数据的搜索查找上有独特的优势。那么究竟是不是这样,二叉搜索树又是否有更多优势呢?让我们来一探究竟。
1.二叉搜索树的概念
二叉搜索树又称二叉排序树,它具有两种情况,空树和非空树。空树当然没有什么好谈的,我们具体要介绍的是非空树。
当二叉搜索树为非空树时,它具有以下性质:
• 若它的左子树不为空,则左子树上所有结点的值都小于等于根结点的值
• 若它的右子树不为空,则右子树上所有结点的值都大于等于根结点的值
• 它的左右子树也分别为二叉搜索树
• 二叉搜索树中可以支持插入相等的值,也可以不支持插入相等的值,具体看使用场景
2.二叉搜索树的构建(插入)
实际上二叉搜索树从无到有的插入过程就是二叉搜索树的构建过程
给出以下数字: 8、3、1、10、6、4、7、14、13,我们来画一个二叉搜索树
插入的具体过程如下:
-
树为空,则直接新增结点,赋值给root
-
树不空,按二叉搜索树性质,插入值比当前结点大往右走,插入值比当前结点小往左走,找到空位
置,插入新结点。
- 如果支持插入相等的值,插入值跟当前结点相等的值可以往右走,也可以往左走,找到空位置,插
入新结点。(要注意的是要保持逻辑一致性,插入相等的值不要一会往右走,一会往左走)
让我们按照以上步骤来画一个二叉搜索树吧
首先是根节点8,然后插入3,3小于8,往左走

1小于8,往左走,小于3,往左走

10大于8,往右走
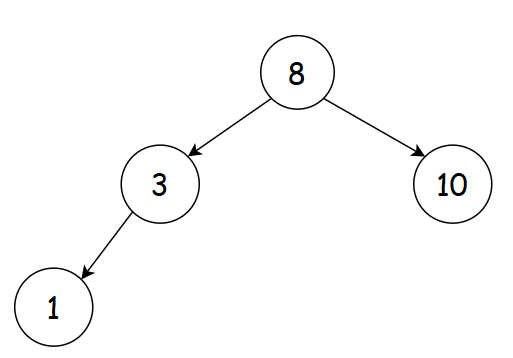
6小于8,往左走,大于3,往右走

4小于8,往左走,大于3,往右走,小于6,往左走

7小于8,往左走,大于3,往右走,大于6,往右走

14大于8,往右走,大于10,往右走

13大于8,往右走,大于10,往右走,小于14,往左走

由此,我们已经画完了一个完整的二叉搜索树
下面便是二叉搜索树基本框架的代码实现,由于与二叉树类似,因此不再过多赘述
#include<iostream>
using namespace std;
//K代指key
//模板,适用于任意数据类型的K
template<class K>
// C++中struct升级成了类
//class定义成员没有被访问限定符修饰时默认为private,struct默认为public。
struct BSTNode
{
K _key;
//BSTNode是类名,BSTNode<K>才是类型
BSTNode<K>* _left;
BSTNode<K>* _right;
//加上引用防止K是容器类型
BSTNode(const K& key)
:_key(key)
,_left(nullptr)
,_right(nullptr)
{}
};
template<class K>
class BSNTree
{
typedef BSTNode<K> Node;
public:
//插入
bool Insert(const K& key)
{
//...
}
//按中序遍历访问
//由于_root在类外不能被访问,因此我们取巧一下,在类里面内嵌一层函数
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
//查找
bool Find(const K& key)
{
//...
}
//删除
bool Erase(const K& key)
{
//...
}
private:
Node* _root=nullptr;
};
接下来,让我们来实现一下二叉搜索树的插入
//...
//插入
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
//小于(=),往左走
if (key <= cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
//大于,往右走
parent = cur;
cur = cur->_right;
}
}
//此时,cur位置是空,可以插入,但cur是局部变量,因此新节点不能给cur
//需要根据parent选择新节点的插入位置
if (key <= parent->_key)
{
parent->_left = new Node(key);
return true;
}
else
{
parent->_right = new Node(key);
return true;
}
}
//...
void test1()
{
BSNTree<int> t;
int a[] = { 8,3,1,10,6,4,7,14,13 };
for (auto& e : a)
{
t.Insert(e);
}
t.InOrder();
//让我们再来尝试下存在冗余(相等)的情况
BSNTree<int> t1;
int a1[] = { 1,6,8,3,1,10,6,4,7,14,13 };
for (auto& e : a1)
{
t1.Insert(e);
}
t1.InOrder();
}
int main()
{
test1();
return 0;
}
在二叉搜索树中还有一个有趣的巧合,如果你用中序遍历(左根右)去访问它,你会发现它是以升序序列排列的,如:
1、3、4、6、7、8、10、13、14,而这个巧合也能够帮助我们更为方便的检验我们所构建的二叉搜索树是否正确

3.二叉搜索树的查找
二叉搜索树的查找就简单多了,根据传入的参数key,key小于当前节点值,往左走,大于当前节点值,往右走
找到了,返回true,没找到,返回false
代码如下:
//...
//查找
bool Find(const K& key)
{
if (_root == nullptr)
return false;
Node* cur = _root;
while (cur)
{
if (key == cur->_key)
return true;
else if (key < cur->_key)
cur = cur->_left;
else
cur = cur->_right;
}
return false;
}
//
void test1()
{
BSNTree<int> t;
int a[] = { 8,3,1,10,6,4,7,14,13 };
for (auto& e : a)
{
t.Insert(e);
}
t.InOrder();
//让我们再来尝试下存在冗余(相等)的情况
BSNTree<int> t1;
int a1[] = { 1,6,8,3,1,10,6,4,7,14,13 };
for (auto& e : a1)
{
t1.Insert(e);
}
t1.InOrder();
cout << t.Find(8) << endl;
cout << t.Find(9) << endl;
}
int main()
{
test1();
return 0;
}

4.二叉搜索树的删除
咚咚咚(敲黑板),注意了注意了,接下来就是二叉搜索树的重难点了,二叉搜索树的删除,一定要认真听讲哦
既然要删除某个元素,那前提自然是该元素存在于二叉搜索树中,因此要首先查找元素是否在二叉搜索树中,如果不存在,则返回false。
如果查找到元素存在则分以下四种情况分别处理:(假设要删除的结点为N)
- 要删除结点N左右孩子均为空
解决方案:
把N结点的父亲对应孩子指针指向空,直接删除N结点(情况1可以当成2或者3处理,效果是一样
的)

- 要删除的结点N左孩子为空,右孩子结点不为空
解决方案:
把N结点的父亲对应孩子指针指向N的右孩子,直接删除N结点

- 要删除的结点N右孩子位空,左孩子结点不为空
解决方案:
把N结点的父亲对应孩子指针指向N的左孩子,直接删除N结点

- 要删除的结点N左右孩子结点均不为空
解决方案:
无法直接删除N结点,因为N的两个孩子无处安放,只能用替换法删除。找N左子树的值最大结点R(最右结点)或者N右子树的值最小结点R(最左结点)替代N(保证替换后N的左子树都小于N,N的右子树都大于N),因为这两个结点中任意一个,放到N的位置,都满足二叉搜索树的规则。替代N的意思就是N和R的两个结点的值交换,转而变成删除R结点,R结点符合情况2或情况3,可以直接删除。

R若是N左子树的值最大结点R(最右结点****),则R不会有右孩子
R若是N右子树的值最小结点R(最左结点),则R不会有左孩子

实际上删除节点只分为3种情况就可以了,将1,与2,或3结合在一起
代码如下:
//...
//删除
bool Erase(const K& key)
{
//删除当前节点时,需借助其父节点
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
//先找到要删除的节点
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else
{
//开始删除
//左孩子为空及左右孩子均为空
//把cur结点的父亲对应孩子指针指向cur的右孩子,直接删除cur结点
if (cur->_left==nullptr)
{
//特殊情况
if (cur == _root)
{
//此时有两种情况,一是二叉搜索树只有一个根节点,直接将_root赋为nullptr
//二是二叉搜索树只有右孩子,则需将右孩子赋给根节点
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
//要删除的结点cur右孩子位空,左孩子结点不为空
//特殊情况
if (cur == _root)
{
//二叉搜索树只有左孩子,则需将左孩子赋给根节点
_root = cur->_left;
}
else
{
//把cur结点的父亲对应孩子指针指向cur的左孩子,直接删除cur结点
if (cur == parent->_left)
parent->_left = cur->_left;
else
parent->_right = cur->_left;
}
delete cur;
}
else
{
//左右孩子均不为空,替换
//找cur右子树的值最小结点R(最左结点)替代cur,
// 替代cur的意思就是cur和R的两个结点的值交换,转而变成删除R结点
Node* Rparent = cur;
Node* R = cur->_right;
while (R->_left)
{
Rparent = R;
R = R->_left;
}
swap(cur->_key, R->_key);
//R若是cur右子树的值最小结点R(最左结点),则R不会有左孩子,只需考虑R的右孩子
if (Rparent->_left == R)
Rparent->_left = R->_right;
else
Rparent->_right = R->_right;
delete R;
}
return true;
}
}
return false;
}
//...
void test1()
{
BSNTree<int> t;
int a[] = { 8,3,1,10,6,4,7,14,13 };
for (auto& e : a)
{
t.Insert(e);
}
t.InOrder();
for (auto e : a)
{
t.Erase(e);
t.InOrder();
}
}
int main()
{
test1();
return 0;
}

完整代码
#include<iostream>
using namespace std;
//K代指key
//模板,适用于任意数据类型的K
template<class K>
// C++中struct升级成了类
//class定义成员没有被访问限定符修饰时默认为private,struct默认为public。
struct BSTNode
{
K _key;
//BSTNode是类名,BSTNode<K>才是类型
BSTNode<K>* _left;
BSTNode<K>* _right;
//加上引用防止K是容器类型
BSTNode(const K& key)
:_key(key)
,_left(nullptr)
,_right(nullptr)
{}
};
template<class K>
class BSNTree
{
typedef BSTNode<K> Node;
public:
//插入
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
//小于(=),往左走
if (key <= cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
//大于,往右走
parent = cur;
cur = cur->_right;
}
}
//此时,cur位置是空,可以插入,但cur是局部变量,因此新节点不能给cur
//需要根据parent选择新节点的插入位置
if (key <= parent->_key)
{
parent->_left = new Node(key);
return true;
}
else
{
parent->_right = new Node(key);
return true;
}
}
//按中序遍历访问
//由于_root在类外不能被访问,因此我们取巧一下,在类里面内嵌一层函数
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
//查找
bool Find(const K& key)
{
if (_root == nullptr)
return false;
Node* cur = _root;
while (cur)
{
if (key == cur->_key)
return true;
else if (key < cur->_key)
cur = cur->_left;
else
cur = cur->_right;
}
return false;
}
//删除
bool Erase(const K& key)
{
//删除当前节点时,需借助其父节点
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
//先找到要删除的节点
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else
{
//开始删除
//左孩子为空及左右孩子均为空
//把cur结点的父亲对应孩子指针指向cur的右孩子,直接删除cur结点
if (cur->_left==nullptr)
{
//特殊情况
if (cur == _root)
{
//此时有两种情况,一是二叉搜索树只有一个根节点,直接将_root赋为nullptr
//二是二叉搜索树只有右孩子,则需将右孩子赋给根节点
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
//要删除的结点cur右孩子位空,左孩子结点不为空
//特殊情况
if (cur == _root)
{
//二叉搜索树只有左孩子,则需将左孩子赋给根节点
_root = cur->_left;
}
else
{
//把cur结点的父亲对应孩子指针指向cur的左孩子,直接删除cur结点
if (cur == parent->_left)
parent->_left = cur->_left;
else
parent->_right = cur->_left;
}
delete cur;
}
else
{
//左右孩子均不为空,替换
//找cur右子树的值最小结点R(最左结点)替代cur,
// 替代cur的意思就是cur和R的两个结点的值交换,转而变成删除R结点
Node* Rparent = cur;
Node* R = cur->_right;
while (R->_left)
{
Rparent = R;
R = R->_left;
}
swap(cur->_key, R->_key);
//R若是cur右子树的值最小结点R(最左结点),则R不会有左孩子,只需考虑R的右孩子
if (Rparent->_left == R)
Rparent->_left = R->_right;
else
Rparent->_right = R->_right;
delete R;
}
return true;
}
}
return false;
}
private:
Node* _root=nullptr;
};
void test1()
{
BSNTree<int> t;
int a[] = { 8,3,1,10,6,4,7,14,13 };
for (auto& e : a)
{
t.Insert(e);
}
t.InOrder();
让我们再来尝试下存在冗余(相等)的情况
BSNTree<int> t1;
int a1[] = { 1,6,8,3,1,10,6,4,7,14,13 };
for (auto& e : a1)
{
t1.Insert(e);
}
t1.InOrder();
cout << t.Find(8) << endl;
cout << t.Find(9) << endl;*/
for (auto e : a)
{
t.Erase(e);
t.InOrder();
}
}
int main()
{
test1();
return 0;
}
4.二叉搜索树的性能分析
最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其高度为: log2 N
最差情况下,二叉搜索树退化为单支树(或者类似单支),其高度为: N
所以综合而言二叉搜索树增删查改时间复杂度为: O(N)
到此,二叉搜索树的插入、删除、查找就讲完了,怎么样,是不是感觉大脑里面多了很多新知识。
如果觉得博主讲的还可以的话,就请大家多多支持博主,收藏加关注,追更不迷路
如果觉得博主哪里讲的不到位或是有疏漏,还请大家多多指出,博主一定会加以改正
博语小屋将持续为您推出文章
























 2175
2175

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








