小杰机器学习（three）——前向传播、反向传播、权重与偏置、损失函数（均方误差，求损失函数方法之一）、梯度下降（梯度+优化显示过程）、优化器。

1.前向传播

        前向传播是指在一个机器学习算法中，从输入到输出的信息传递过程，具体来说，就是在数据输入后，经过一系列的运算后得到结果的过程。

输入x 经过一系列计算f(x) 得到y的过程

        比如y=2x+3,这个公式，前向传播就是通过给定x,根据公式2x+3得到输出结果y的值的过程就是前向传播。

        对数据的输入逐步处理，提取对应的特征，并进行预测。

（1） 输入

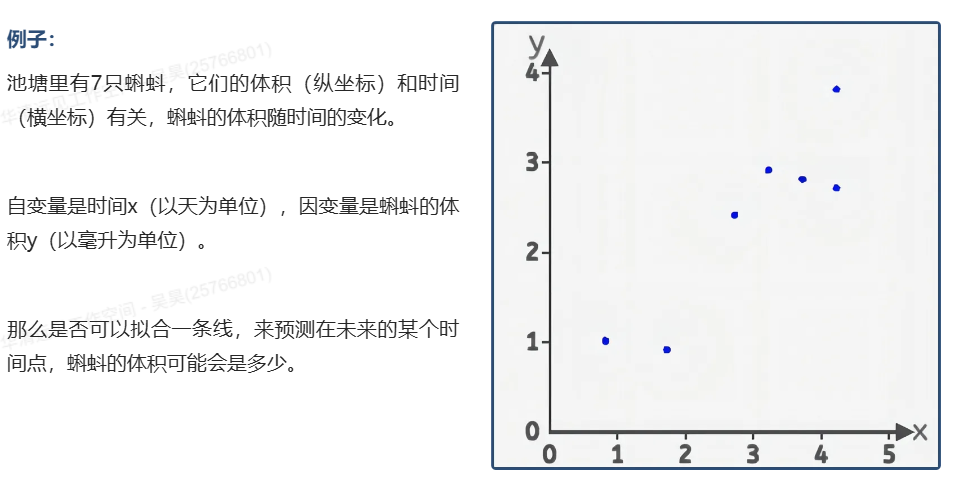
（2）前向计算

        前向传播是指在一个机器学习算法中，从输入到输出的信息传递过程，具体来说，就是在数据输入后，经过一系列的运算后得到结果的过程。

        在本实验中，为了使用直线来拟合上面7个散点，可以用直线的斜截式方程来进行拟合，给出直线公式：

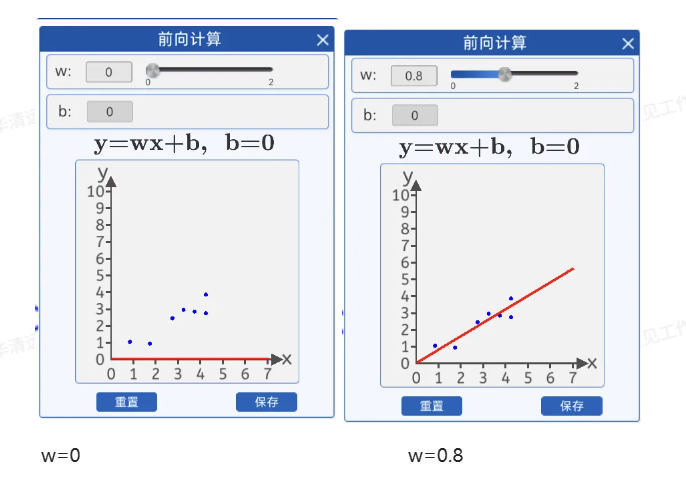
虚拟仿真中限制了w和b的范围：

在前向计算中，为了简化运算，我们固定b的值为0，而w的值可以任意修改（范围0-2）。

w（weight）：权重

b（bias）：偏置

        也就是说，我们是用一条过原点的直线来拟合这些散点，在该组件中修改w的值可以实时看到直线与散点的位置关系。

（3）单点误差

        由下图可知，当w等于2的时候“拟合”这些散点的效果并不好，和实际的坐标点y轴有一些差距。

         目标获得每一个数据点损失。

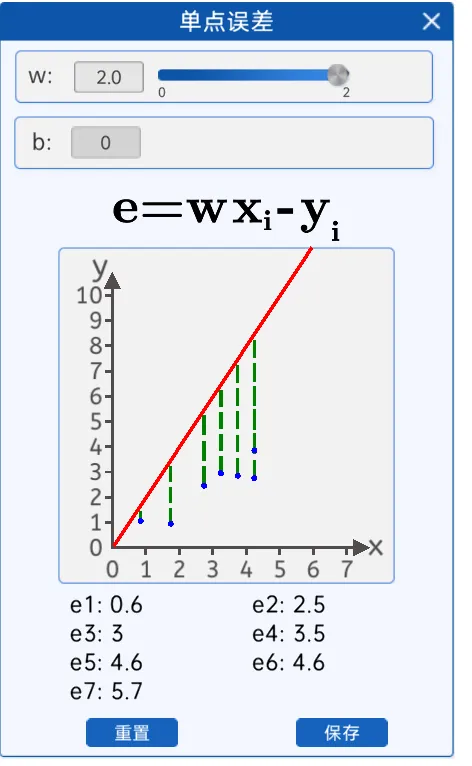
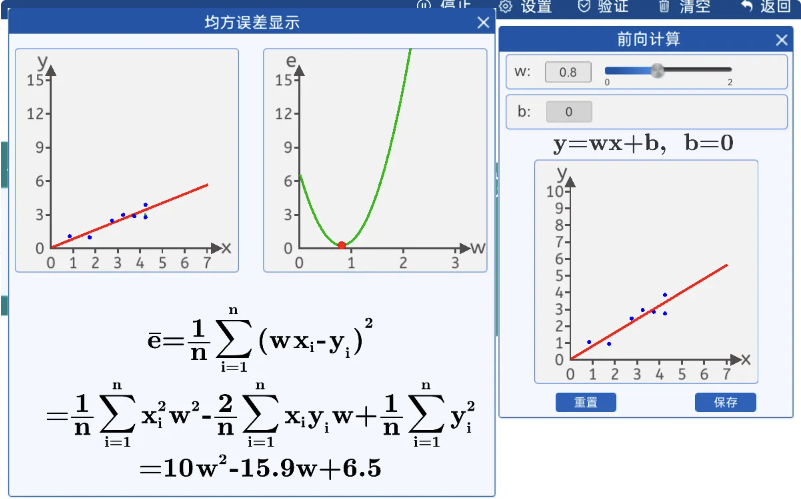
（4） 均方误差

        损失函数的概念：

        损失函数（Loss Function）是用来衡量模型预测结果与实际结果之间的差异的一种函数。在机器学习中，损失函数通常被用来优化模型，通过最小化损失函数来提高模型的预测准确率。

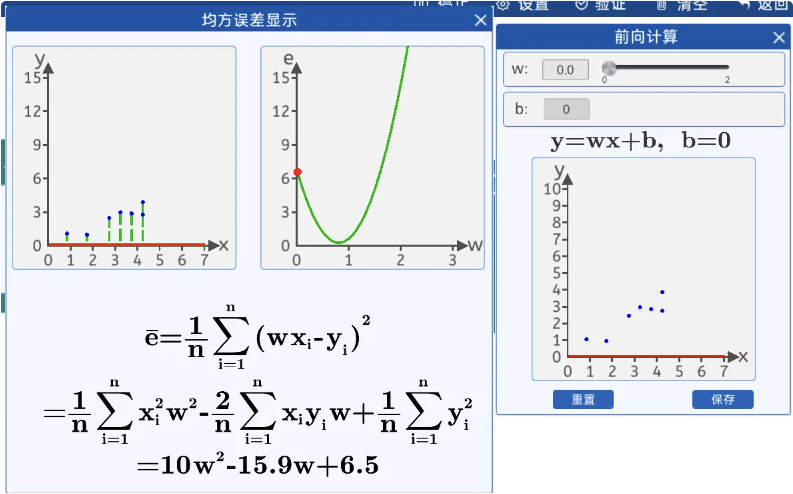
        由上图得知，w=0.8的损失函数值，拟合效果更好，于是根据这些散点，我们拟合出了一条直线y=0.8x，这样通过时间来判断蝌蚪生长体积和天数的关系。

2. 前向传播的过程

        实际的前向传播远比上面的例子复杂，下面是前向传播的分层说明：

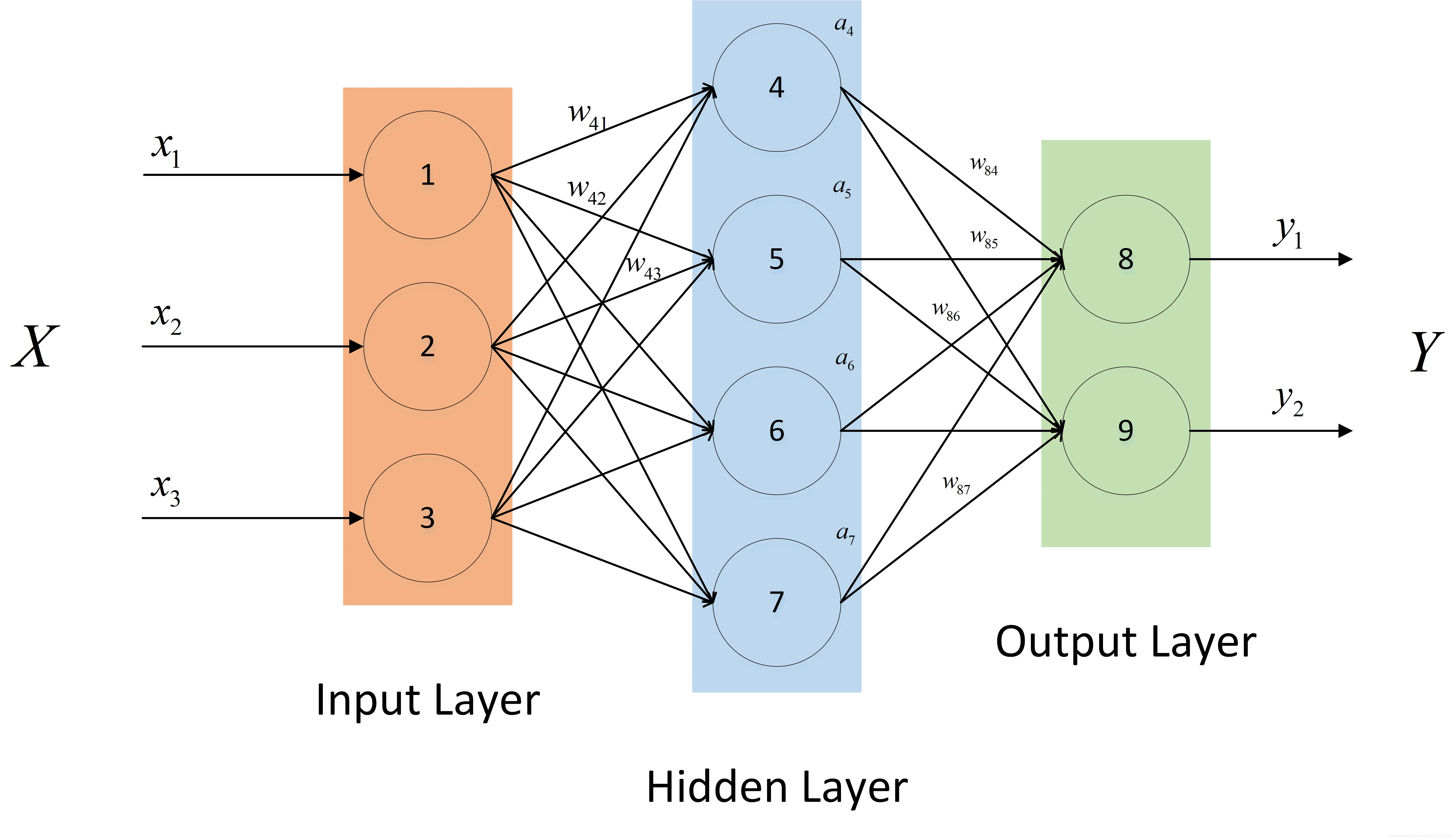
step1：输入层

输入数据首先需要进入输入层，每一个神经元都会接收一个信号(输入值(矩阵))

在本例中输入就是x

step2：输入层到隐藏层

输入层的输出作为下一层的(通常是隐藏层)，通过与权重相乘加上偏置项后进行非线性变换‌，使用激活函数对隐藏层的输出进行非线性变换，以引入非线性特性，增强模型的表达能力。

在本例中w就是特征。

step3：隐藏层到输出层

将隐藏层的输出乘以隐藏层到输出层的权重矩阵，再加上偏置，计算输出层的输出。

在本例中输出就是y

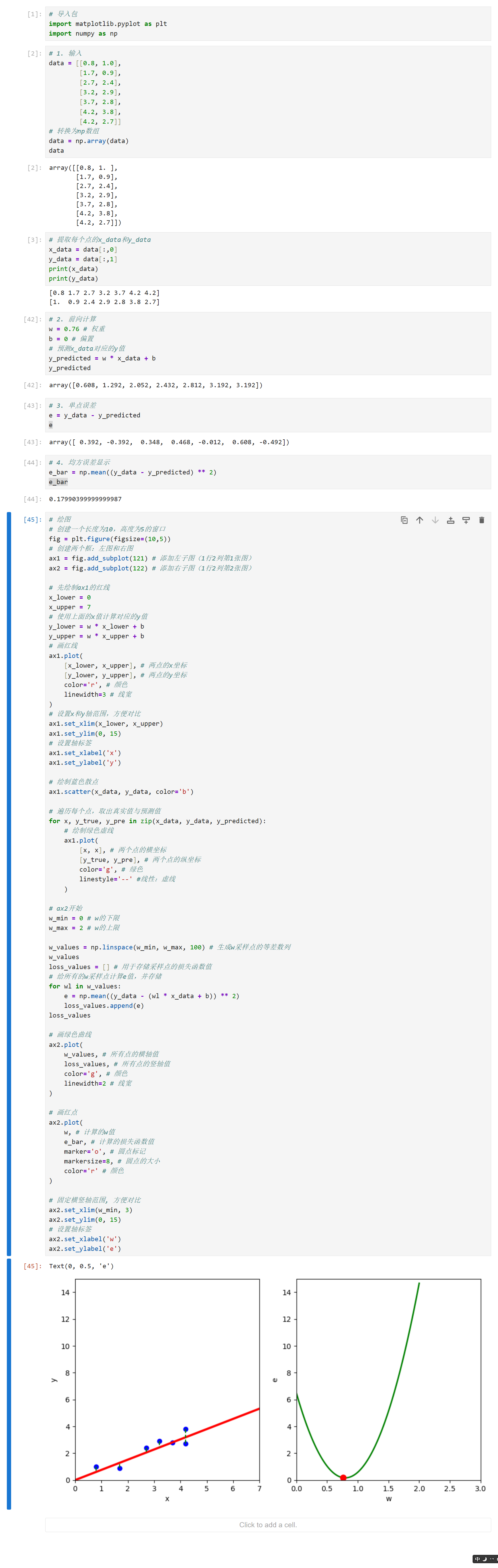
 代码

3.反向传播

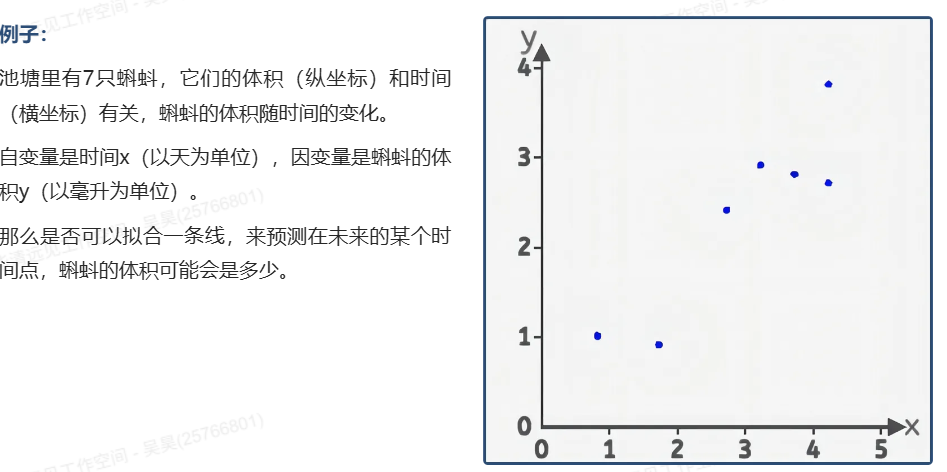
（1） 案例导入

4.前向传播与反向传播的区别

        前向传播是在参数固定后，向公式中传入参数，进行预测的一个过程。当参数值选择的不恰当时，会导致最后的预测值不符合我们的预期，于是我们就需要重新修改参数值。在前向传播实验中时，我们都是通过手动修改w值来使直线能更好的拟合散点。

        反向传播是在前向传播后进行的，它是对参数进行更新的一个过程，反向传播的过程中参数会根据某些规律修改从而改变损失函数的值。

5.反向传播实验过程

（1）损失函数

        给出直线公式y=wx+b，令 b=0。在前向传播时，得到均方差损失函数，根据该表达式，可以发现，损失函数是一个关于w的一元二次方程：

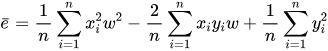
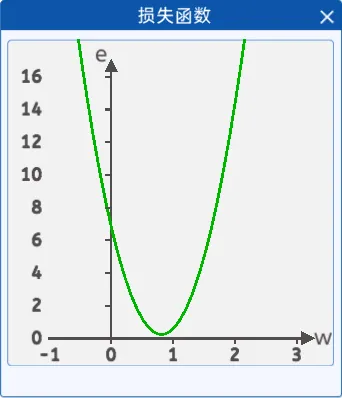
（2）参数初始化

        反向传播自己会不断的修改参数，即w，那么刚开始时，需要给w一个初始化的值(这个初始化的值可以是任意的值)，初始化方式可以有随便给一个数或者让代码随机定一个，后续损失的值会根据优化算法来更新w。

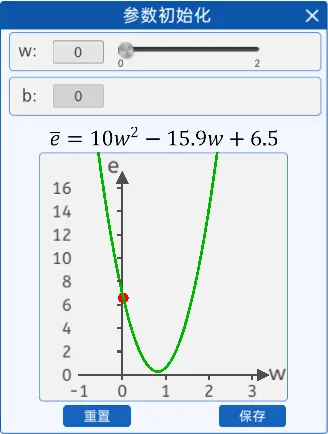
（3）梯度+优化过程显示=梯度下降

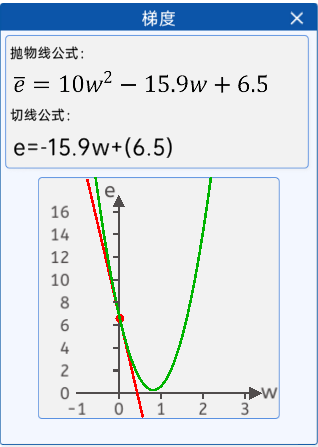
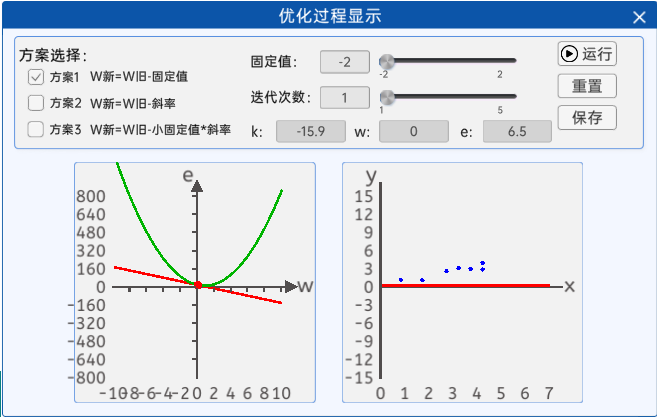
        3.1优化方法（优化器）

在损失函数关于w的表达式中，确实存在一个w，使得损失函数的值最小。下面使用三种方案，包括固定值法、斜率法、小固定值*斜率法，展示一下其不同的优化效果。

        1. 固定值法

        在更新w的时候，采用旧的w减去一个固定的值的方法其公式如下所示：

        固固定值的弊端有两个：

1. 方向性不确定

        当固定值的正负确定后，就意味着w的更新方向确定了，比如w>0时，且固定值为正数时，w的值是不断减小的，w<0时，固定值为负数时，w的值是不断变大的。

2. 准确性不佳

        不能够准确的更新到令损失值最小的w值，比如最合适的w值为0.8，现在的w值为1，而固定值为0.5，那么就会跳过0.8，直接变成0.5，并且如果还没迭代完，还会变成0，-0.5，…。

也就是说，想通过该方法更新到最好的w值，要么事先算好，要么碰运气，总之效果很差。

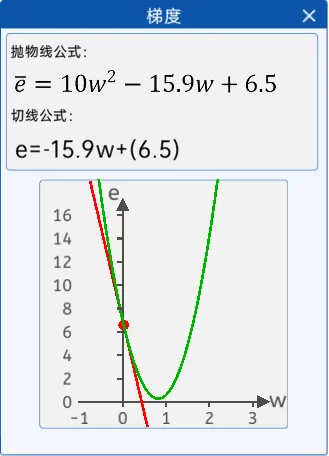
        2.斜率法

        在这里它就是损失函数曲线中的w点的切线，斜率还有个很好的特性，那就是当w小于最低点对应的w时，它是负的；当w大于最低点对应的w时，它是正的。

        在迭代w的过程中，分为两种情况：

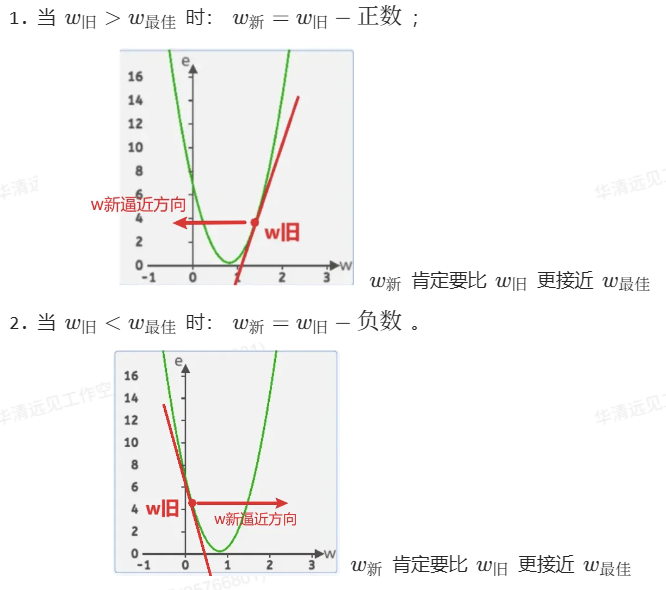
如果只考虑斜率正负号，整合公式如下所示：

斜率法的弊端：

        当损失函数比较陡峭时，斜率值很大，会来回震荡，并且斜率值越来越大，损失函数值也会越来越大，效果也不是很理想。

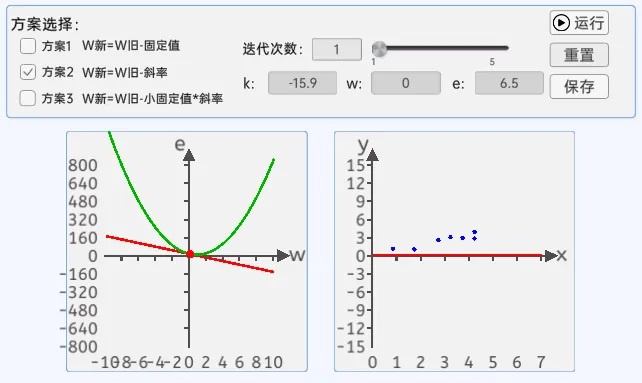
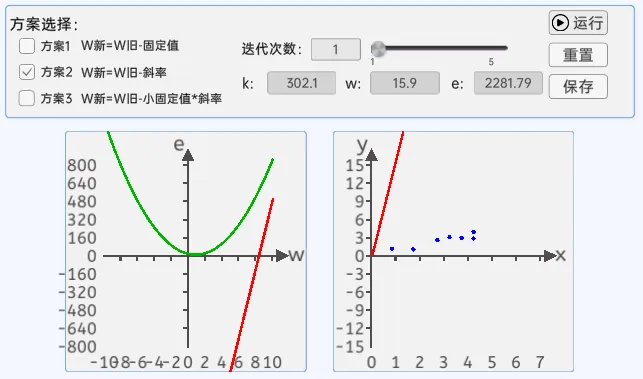
        3.小固定值*斜率

        斜率有很好的特性，但是斜率值太大了不受控制，那么是不是可以把斜率，也就是梯度的值乘以一下很小的数（小于1）。其公式如下所示：

        式子中的小固定值被称为学习率，通过改变学习率的值能调整w的更新速度，而整个式子就叫做梯度下降（Gradient Descent，GD），是一种优化函数，作用是最小化损失函数。

        3.2学习率（Learning Rate）

        在机器学习和深度学习中，学习率是一个超参数，用于控制权重(w)更新的速度。通常来说，学习率越大，参数更新就越快，模型就学习的越快，但如果学习率过大，模型可能会不稳定，甚至无法收敛到最优解。学习率越小，参数更新就越慢，模型学习的就越慢，但如果学习率过小，模型可能在有限的时间下无法找到最优解。

因此，确定一个合适的学习率是非常重要的。

        3.3 梯度

        在机器学习中，梯度表示损失函数对于模型参数的偏导数，梯度下降是机器学习中一种常用的优化算法。

                它的基本思想是在训练过程中通过不断调整参数，使损失函数（代表模型预测结果与真实结果之间的差距）达到最小值。

        为了实现这一目标，梯度下降算法会计算损失函数的梯度（带方向的斜率），然后根据梯度的方向更新权重，使损失函数不断减小。

        对于一个模型来说，我们可以计算每一个权重对损失函数的影响程度，然后根据损失函数的梯度来更新这些权重。通过不断重复这一过程，我们就可以找到一组使损失函数最小的权重值，从而训练出一个优秀的模型。

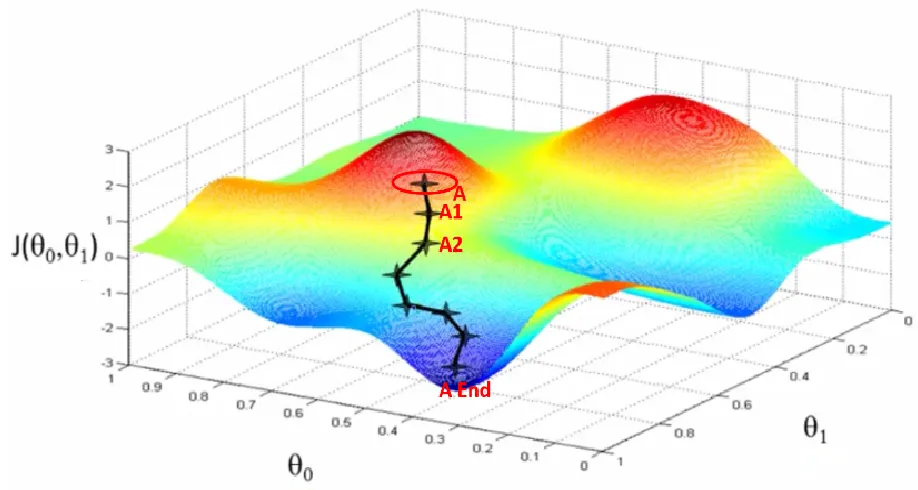
        假设你在一个陌生的山地上，你想找到一个谷底，那么肯定是想沿着向下的坡行走，如果想尽快的走到谷底，那么肯定是要沿着最陡峭的坡下山。每走一步，都找到这里位置最陡峭的下坡走下一步，这就是梯度下降。在这个比喻中，梯度就像是山上的坡度，告诉我们在当前位置上地势变化最快的方向。为了尽快走向谷底，我们需要沿着最陡峭的坡向下行走，而梯度下降算法正是这样的方法。每走一步，我们都找到当前位置最陡峭的下坡方向，然后朝着该方向迈进一小步。这样，我们就在梯度的指引下逐步向着谷底走去，直到到达谷底（局部或全局最优点）。

        通过计算损失函数对参数的梯度，梯度下降算法能够根据梯度的信息来调整参数，朝着减少损失的方向更新模型，从而逐步优化模型，使得模型性能更好。

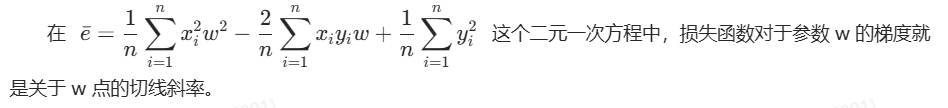
        代码

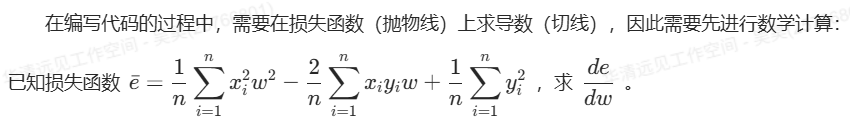
# 导入相关库
import matplotlib.pyplot as plt
# IPython是一个交互式Python环境，配合Jupyter可以提供动态显示功能。
from IPython import display
import numpy as np
import time
[3]
# 1. 输入
data = [[0.8, 1.0],
        [1.7, 0.9],
        [2.7, 2.4],
        [3.2, 2.9],
        [3.7, 2.8],
        [4.2, 3.8],
        [4.2, 2.7]]
# 转换为np数组
data = np.array(data)
data
# 提取每个点的x_data和y_data
x_data = data[:,0]
y_data = data[:,1]
print(x_data)
print(y_data)
[0.8 1.7 2.7 3.2 3.7 4.2 4.2]
[1.  0.9 2.4 2.9 2.8 3.8 2.7]

[4]
# 2. 损失函数
def loss_function(w, b, x_data, y_data):
    # 通过x预测y的值
    y_predicted = w * x_data + b
    # 计算均方误差
    e_bar = np.mean((y_data - y_predicted) ** 2)
    return e_bar
[17]
# 3. 参数初始化
w = 1.0
b = 0
# 4. 梯度 + 5. 优化显示过程 = 梯度下降
# w新 = w旧 - 学习率 * 斜率
w_old = w # 第一次的w旧使用初始参数
learning_rate = 0.01 # 学习率
# 创建窗口子图
# 返回值fig：总窗口对象
# ax1,ax2:子图
fig,(ax1, ax2) = plt.subplots(
    1, # 1行
    2, # 2列 
    figsize=(12, 6) # 宽高
)

# 子图1的w轴（横轴）采样
w_values = np.linspace(-10, 10, 200) # -10到10，采样200个点
w_values

# 计算上面采样点的损失函数
loss_values = []
for w in w_values:
    loss_values.append(loss_function(w, b, x_data, y_data))
loss_values

# 迭代器次数
num_iterations = 50

# 子图2中x轴的范围，后面会反复用到
ax2_x_axis_min = 0
ax2_x_axis_max = 7

# 重置静态区域
def initialize_axes():
    # 清空Jupyter输出
    display.clear_output(wait=True) # 清空画布不等待
    # 清空子图内容
    ax1.cla()
    ax2.cla()

    # 重新设置两个子图的坐标轴尺寸等信息
    ax1.set_xlim(-10, 10)
    ax1.set_ylim(-800, 800)
    ax1.set_xlabel('w')
    ax1.set_ylabel('e')
    ax1.set_title('Loss Function')
    # 绘制损失函数绿曲线
    # 画绿色曲线
    ax1.plot(
        w_values, # 所有点的横轴值
        loss_values, # 所有点的竖轴值
        color='g', # 颜色
        linewidth=2 # 线宽
    )

    ax2.set_xlim(ax2_x_axis_min, ax2_x_axis_max)
    ax2.set_ylim(-15, 15)
    ax2.set_xlabel('x')
    ax2.set_ylabel('y')
    ax2.set_title('Data Scatter and Fitted Line') # 数据散点和拟合线
    ax2.scatter(x_data, y_data, color='b') # 绘制散点

# 循环迭代进行反向传播并绘制
for i in range(num_iterations + 1):
    initialize_axes()
    # 计算损失函数
    e_bar = loss_function(w_old, b, x_data, y_data)
    # 绘制左图红点
    ax1.plot(
        w_old,
        e_bar,
        marker='o',
        markersize=8,
        color='r'
    )

    # 【注意】此处套用上节的de/dw的公式
    de_dw = 2 * np.mean((x_data ** 2)*w_old) - 2 * np.mean(x_data * y_data)
    # e = kw + b → b = e - kw
    intercept = e_bar - de_dw * w_old

    # 拿之前200个采样的w，计算出200个切线上的e，使用200个点连成一条线
    # e = kw + b
    line = de_dw * w_values + intercept
    # 绘制“切线”
    ax1.plot(
        w_values, # 所有点的横轴值
        line, # 所有点的竖轴值
        color='r', # 颜色
        linewidth=2 # 线宽
    )
    # 左图绘制完成，开始右图绘制红线
    y_lower_right = w_old * ax2_x_axis_min + b # 红线左端点的竖轴值
    y_upper_right = w_old * ax2_x_axis_max + b # 红线右端点的竖轴值
    
    # 绘制红线
    ax2.plot(
        [ax2_x_axis_min, ax2_x_axis_max], # 绘制的直线两端点的x轴数值
        [y_lower_right, y_upper_right], # 绘制的直线两端点的y轴数值
        color='r', # 红色
        linewidth=2 # 线宽
    )

    # 方案选择：方案3——梯度下降
    w_new = w_old - learning_rate * de_dw
    w_old = w_new
    print(w_new)
    
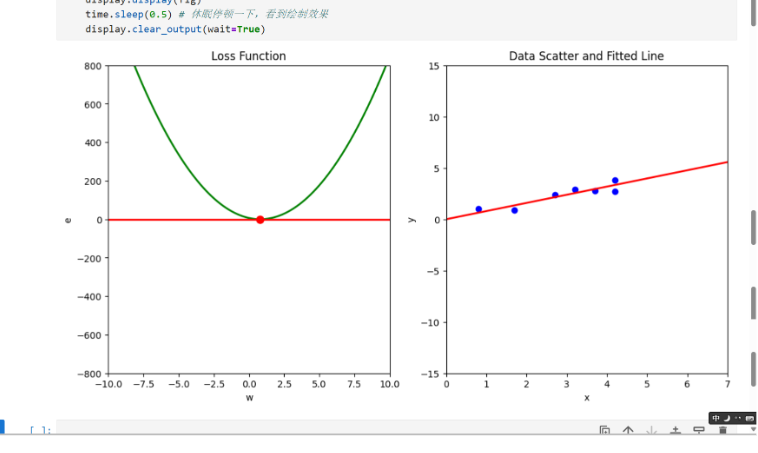
    # 显示图形
    display.display(fig)
    time.sleep(0.5) # 休眠停顿一下，看到绘制效果
    display.clear_output(wait=True)