一、深度学习
1. 深度学习是什么
深度学习(Deep Learning)是机器学习(Machine Learning)的一个研究方向,而机器学习属于人工智能(AI, Artificial Intelligence)的范畴,人工智能是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。
三者的关系可以参考以下这张图。
-
人工智能(AI)是指将机器或计算机程序赋予类似于人类智能的能力,即可以像人一样感知、理解、学习、推理和创造。
-
机器学习(Machine Learning,简称ML)是人工智能中的一种方法和技术,通过让计算机从数据中学习模式和规律,从而不需要人类明确地编写特定的程序来完成任务。
-
深度学习(Deep Learning)是一种基于人工神经网络的机器学习技术,通过模拟人脑神经元之间的联系和活动方式,来实现对输入数据进行分析、抽象和处理的能力。

在详细讲解之前,我要为大家分享这份100G人工智能学习资料
包含数学与Python编程基础、深度学习+机器学习入门到实战,计算机视觉+自然语言处理+大模型资料合集,不仅有配套教程讲义还有对应源码数据集。更有零基础入门学习路线,不论你处于什么阶段,这份资料都能帮助你更好地入门到进阶。

需要的兄弟可以按照这个图的方式免费获取
2. 机器学习划分
机器学习按照学习方式又可以划分为无监督学习、监督学习以及强化学习。深度学习中既有无监督学习算法(如GAN)、也有有监督学习算法(如CNN),由于近年来数据、算法、算力的快速发展,已单独形成一个研究分支。

二、深度学习发展
深度学习本质上是神经网络的一种。神经网络技术起源于上世纪五六十年代,当时叫感知机(perceptron),包含有输入层、输出层和隐藏层。含多个隐藏层的多层感知器就是一种深度学习结构,深度学习通过组合低层特征形成更加抽象的高层表示属性类别或特征,以发现数据的分布式特征表示。
1. 发展历程
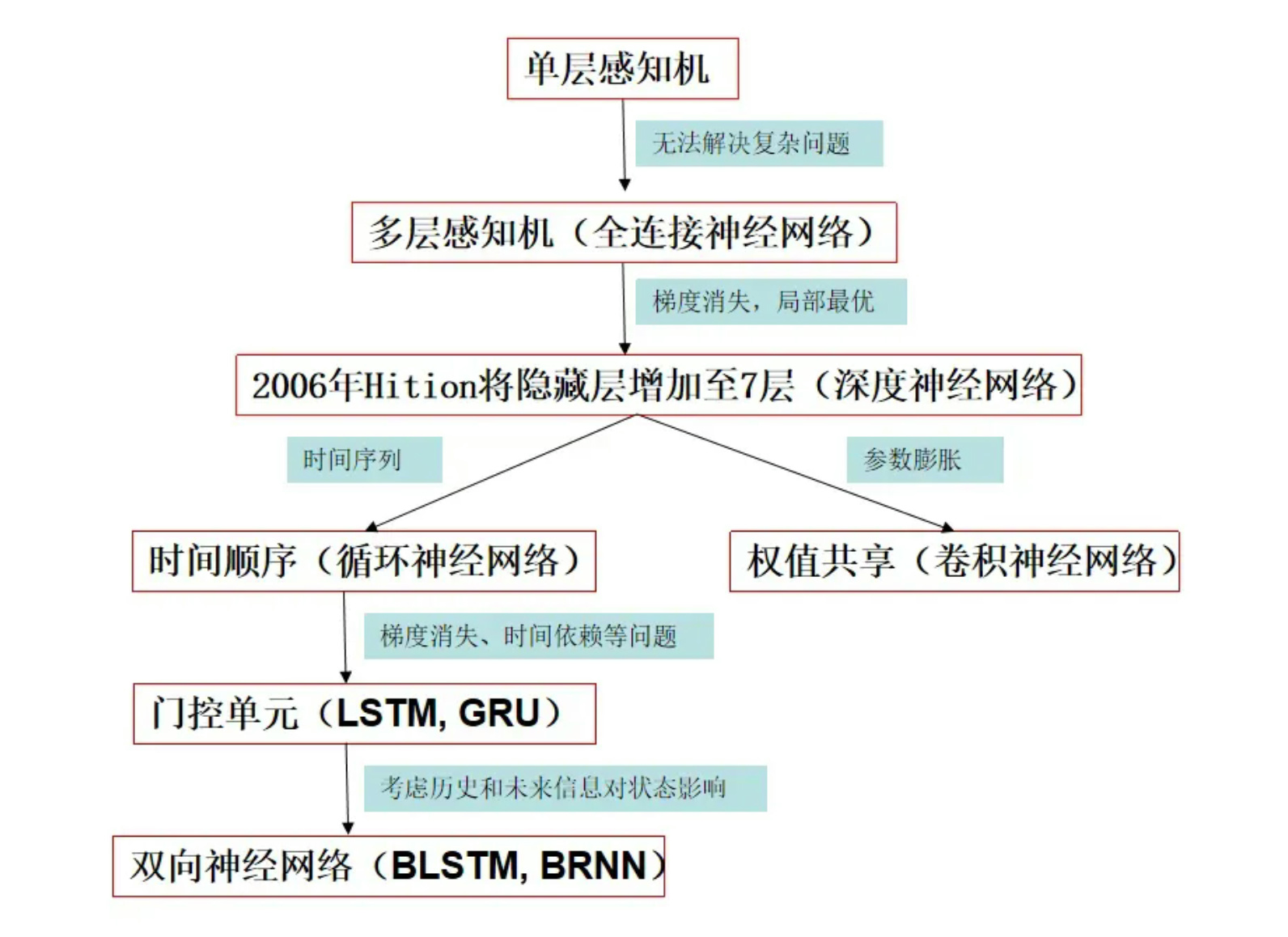
深度学习的发展历程可以参考下图,由单层感知机逐渐发展出RNN, CNN等。
2. 主流研究框架
研究框架如下图有很多,目前主流的是Google的TensorFlow,FaceBook的Pytorch,TensorFlow是一种非常强大和成熟的深度学习库,对生产部署方面比较友好,Pytorch由于其类python代码及动态图及强大的社区,支持快速和动态训练,不过随着版本的迭代,两者功能也都越来越完善。当当然我更推荐新手选择学习PyTorch。

3. 解决什么问题
深度学习主要解决两大类问题:回归和分类


如:
-
房价预测问题(回归)
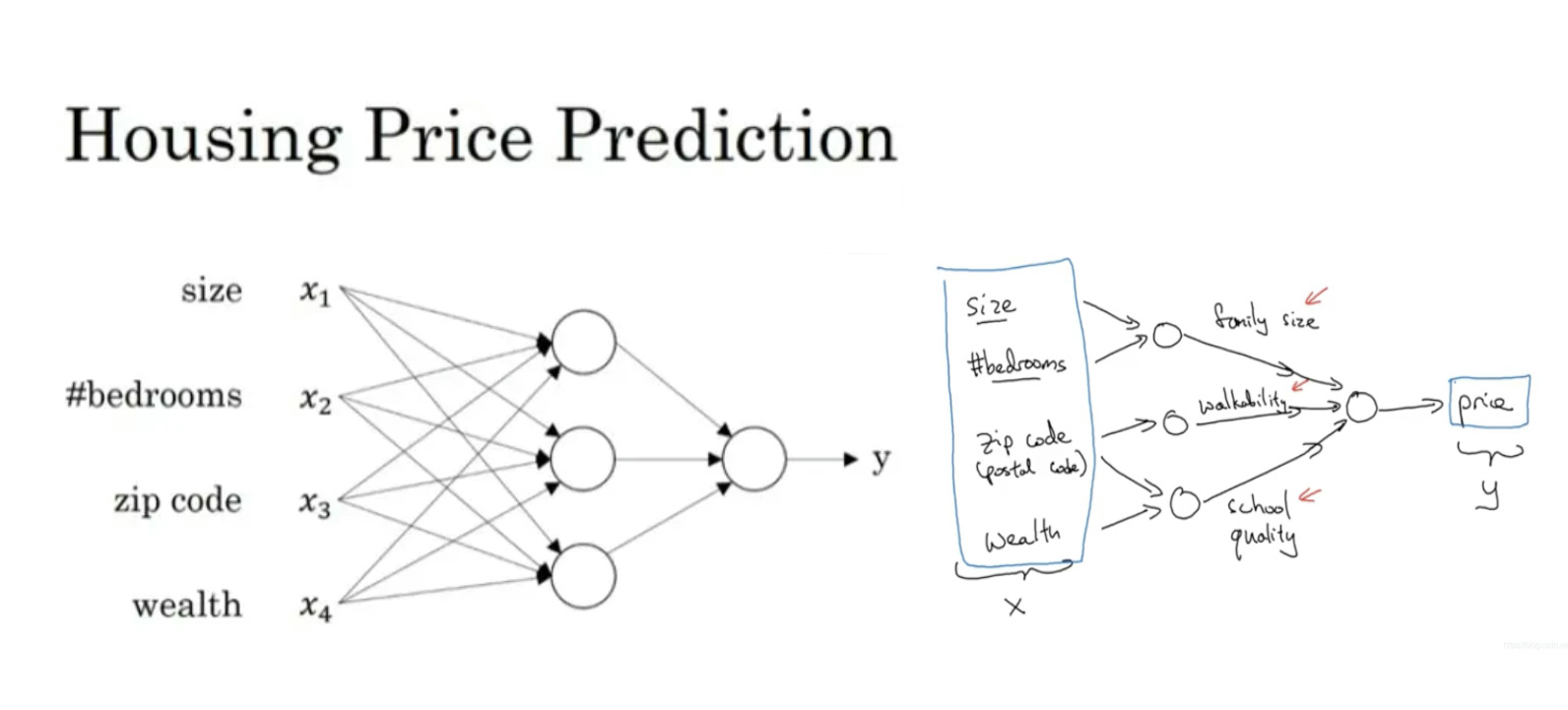
-
目标检测(分类+回归)

4. 实际应用
深度学习现如今在我们生活中的应用随处可见,已经融入到了我们生活各个方面,如:
-
手机人脸解锁、以及人脸安全验证中用到的人脸识别技术, 车牌识别系统等(计算机视觉)。
-
智能音箱的语言识别功能,自动翻译等(自然语言处理)。
-
各种软件的自动推荐功能,如商品、视频等自动推荐(推荐系统)。
-
自动驾驶、智能机器人、工业自动检测、医学图像辅助检测、量化金融等等
最近微软推出的的ChatGPT,以及FaceBook推出的SAM(Segement anything)更是对我们的生活工作带来了更大的变化。
三、基本概念
1. 问题
给定一张64*64大小的RGB图,判断图中是否有猫?

2. 数据转换
这里输入是一张图片,为了运算,我们需要进行如下数值转换:
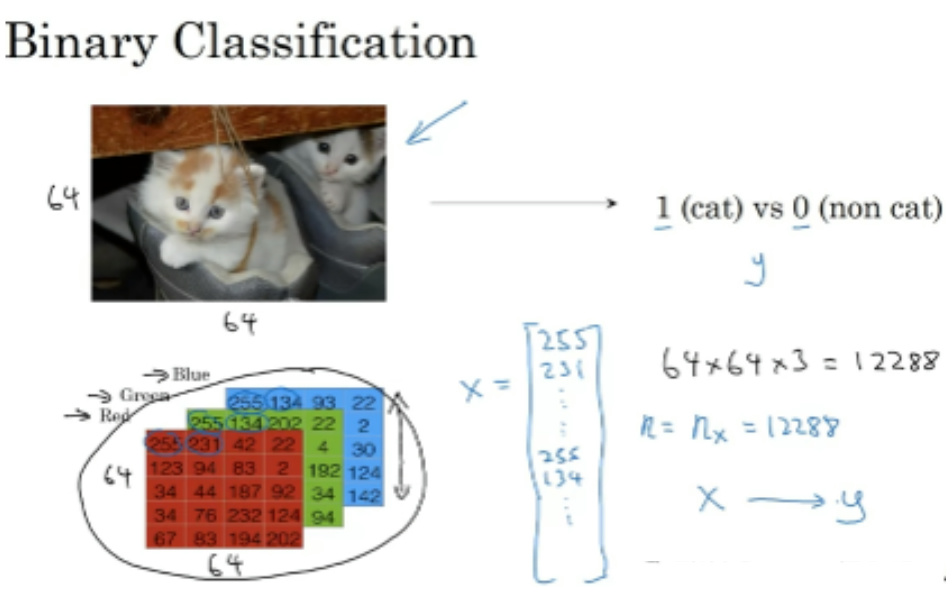
输入:将RGB各通道像素值按顺序排列成一个向量xn,这里展开维度n=12288,
输出:𝑦为1表示有猫,为0表示无猫。
所以问题变成一个求𝑥𝑛到𝑦的一个映射。要求这个映射,我们需要更多的数据样本来学习(训练集)。
进一步,假设我们有𝑚张训练图片,每张图片都有一个对应的标签,即0表示无猫,1表示有猫,数据整合后用矩阵表示如下图。

3. 激活函数
我们这里构建一个简单的网络,求出权重𝑤1,𝑤2,…𝑤𝑚后就可以得到一个从输出到输出𝑌的映射关系𝑓 。

每个样本作为输入通过神经元后得到𝑧=𝑤𝑇𝑥+𝑏,这里得到的𝑧是一个回归后的值,但我们给的标签是0或1,因此需要引入一个函数将数值𝑧转换为0到1之间的一个数𝑧′,即𝑔(𝑧)∈[0,1],在预测过程中给定一个阈值如0.5,如果𝑧′>0.5则预测值𝑦^记为1,否则记为0,进一步我们就可以将预测值变为0/1值。这里的函数采用𝑔(𝑧)=1/+𝑒−𝑧,可以将任意数转换到0到1之间,称为sigmoid函数。
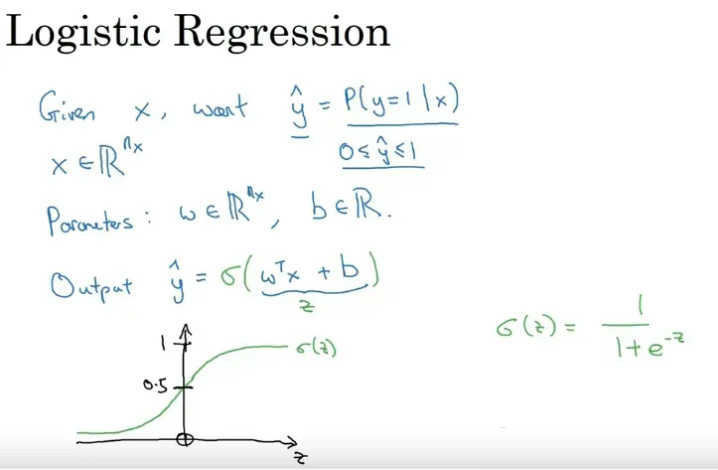
以上的转换函数(sigmoid)称为激活函数,激活函数是向神经网络中引入非线性因素,通过激活函数神经网络就可以拟合各种曲线。
常见的激活函数有以下:
-
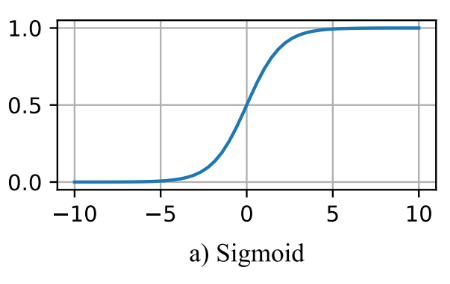
sigmoid 激活函数
函数的定义为:,其值域为 $ (0,1) $。
-
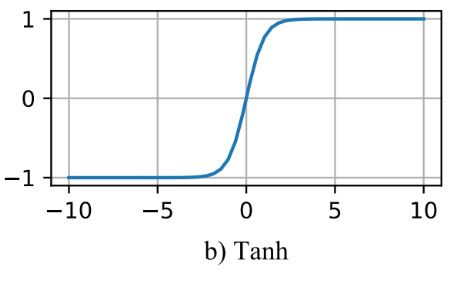
tanh激活函数
函数的定义为:\(f(x) = tanh(x) = \frac{e^x - e{-x}}{ex + e^{-x}}\),值域为 $ (-1,1) $。
-
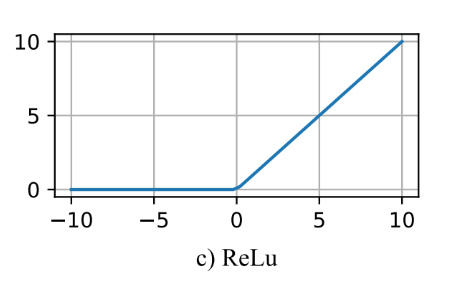
Relu激活函数
函数的定义为:$ f(x) = max(0, x) $ ,值域为 $ [0,+∞) $。
-
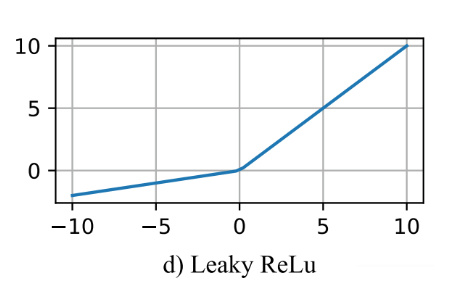
Leak Relu 激活函数
函数定义为:

值域为 $ (-∞,+∞) $。
图像如下($ a = 0.5 $)
-
softmax 函数
函数定义为:\[\sigma(z)_j = \frac{e{z_j}}{\sum_{k=1}K e^{z_k}} \]
Softmax 多用于多分类神经网络输出。
4. 损失函数(代价函数)
经过以上转换后预测值变为0到1的一个概率值,在训练过程中为了评估预测值和真实值的差距,因此我们需要一个函数来进行衡量,在这个例子中,我们可以引用预测值和真实值的二次误差来进行衡量,即:
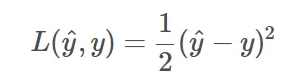
这里的衡量函数就称为损失函数。当然这里当预测值接近0或者1时,损失会非常小,在训练过程中收敛会变慢,因此可以采用交叉熵损失,即:


二次代价函数适合输出神经元是线性的情况,交叉熵代价函数适合输出神经元是S型函数的情况。上述问题中经过sigmoid函数后在0和1时采用二次代价函数值非常小,收敛会变慢。
5. 梯度下降
经过上述步骤,我们现在的问题变成如何调整权重𝑤和偏置𝑏,使得损失函数能够达到最小值。损失函数通常都存在一个下界,在优化过程当中,如果优化算法能够使目标函数不断减小,根据单调有界准则,这个优化算法就能证明是收敛有效的。 只要设计的目标函数有下界,基本上都可以,损失函数非负更为方便,损失函数会比参数高一个维度。

在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。当然这也和初始参数选择有些关系,如下图所示,不同的初始点,最终下降求得的结果可能不一致。
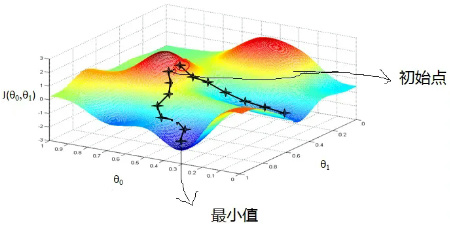
6. 反向传播
经过上面步骤我们知道,要使得损失函数最小,我们需要对参数更新,那如何更新呢?这里引入反向传播,就是从损失函数开始,依次对每个参数求偏导,然后按照链式法则逐步往回更新,其中每次按照梯度方向更新的步长称为学习率。
-
学习率:参数迭代更新的步长
如下图所示,其中𝛼即为学习率
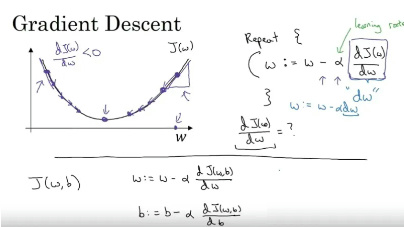
-
链式法则:这个属于高等代数里面偏导数相关内容,用于反向计算相应参数的偏导数 。
由下图所示,从损失函数𝐽逐步反推可以得到其对a,b,c的偏导数。
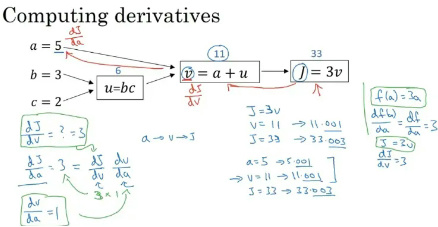
经过以上步骤反复迭代,直到损失函数的误差满足要求或者迭代次数达到设定上限,那么参数就完成了更新,那相应的从𝑥到𝑦的映射也就可以写出来,有了这个映射关系,后续有新得数据来,通过映射关系即可得到一个预测值。
7. 卷积
上述例子中采用的是全连接网络,但实际应用中通常会涉及到卷积神经网络,其中一个重要点就是卷积操作,卷积操作有局部连接和权值共享的特点。依据下图可以理解成一个卷积核在图片上不同位置做卷积会提取到相应的特征。
示例
-
卷积 + padding + bias(局部连接 + 权值共享)
其中padding是边缘填充的意思,有些时候为了和图像边缘进行卷积,需要对图像边缘填充一些像素(如0)。
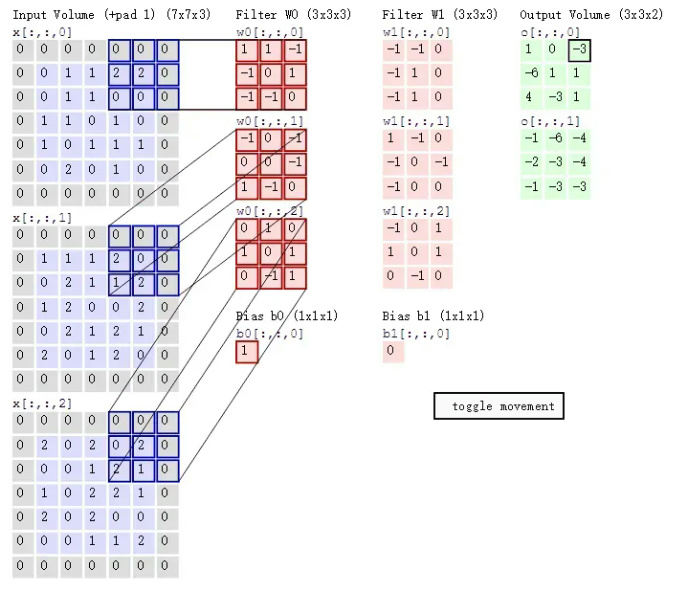
下图显示了两组卷积核对RGB通道卷积的例子。
8. 池化
下图展示的是一个2*2大小的最大池化,即每4个相邻像素选择最大的作为该区域像素值,步长为2,所以这里特征图大小缩减为原来的1/2。

9. 欠拟合 过拟合
我们在训练过程中,如果数据量少或者迭代次数过多,就容易造成过拟合,反之数据量多或者迭代次数不够就容易欠拟合。如下图所示二分类过程中,欠拟合通常具有高偏差,而过拟合通常具有高方差,我们可以依据测试集和训练集的损失来进行判断。


防止过拟合可以采用以下方式:
-
增加数据量
-
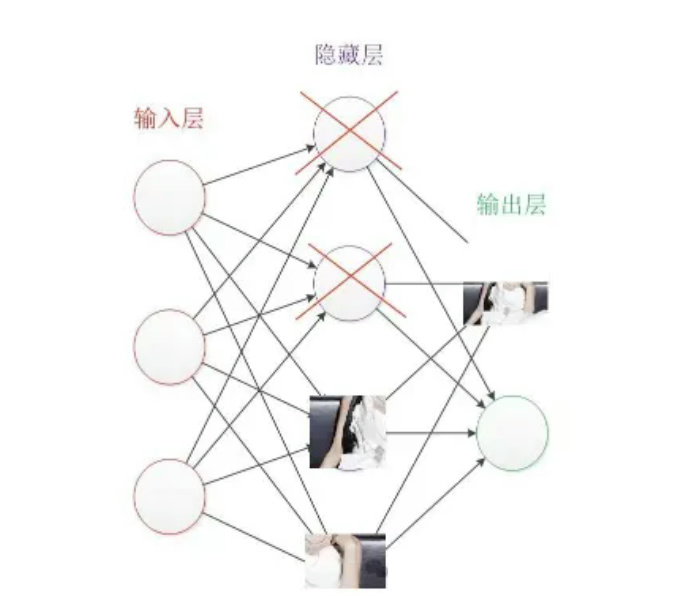
DropOut 正则化
即在训练过程中随机去除部分节点,通俗理解就是不要依赖于任何一个特征,因为该单元的输入可能随时被清除,因此训练后的参数不会偏重于某一个节点进而造成过拟合。
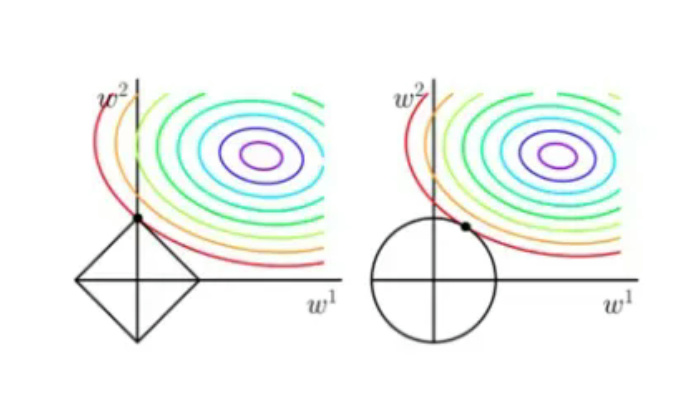
L1 L2正则

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








