光伏MPPT之变步长电导增量法：从原理到实现

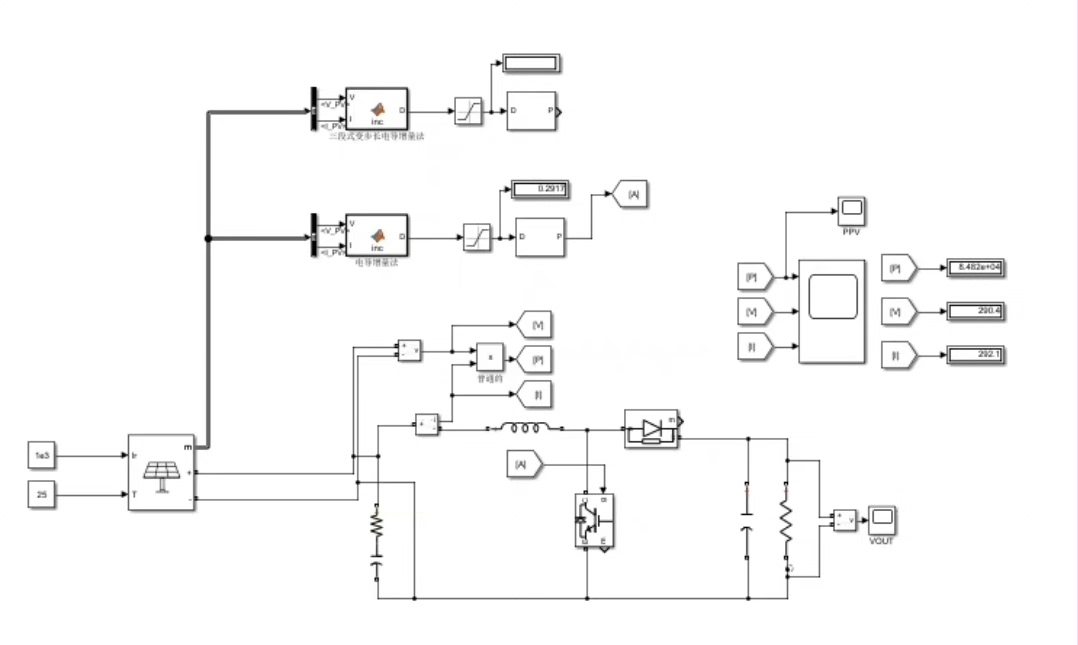
光伏mppt，最大功率点跟踪， 变步长电导增量法，包括变步长电导增量和电导增量两种 模型采用三段式寻优控制变步长电导增量，跟踪效果良好 提供对应的word设计报告 文件版本有matlab22a和18b两种

在光伏系统中，最大功率点跟踪（MPPT）技术至关重要，它能让光伏电池始终工作在最大功率点附近，提升发电效率。今天咱就来唠唠其中的变步长电导增量法，这可是个优化MPPT性能的好法子。

电导增量法基础

电导增量法的核心依据是光伏电池的功率 - 电压曲线特性。大家都知道，光伏电池的输出功率$P$和输出电压$V$之间的关系是一条非线性曲线，存在一个最大功率点。电导增量法就是通过比较功率对电压的微分$\frac{dP}{dV}$与当前电导$G = \frac{I}{V}$ （$I$是电流）的增量$\frac{dG}{dV}$ 来判断工作点与最大功率点的相对位置。

假设光伏电池的输出功率$P = VI$，对$P$关于$V$求导可得：$\frac{dP}{dV} = I + V\frac{dI}{dV}$ 。当 $\frac{dP}{dV} = 0$时，就达到最大功率点。

用代码简单示意一下基础电导增量法的判断逻辑（以Python为例）：

# 假设已经获取到当前电压V，电流I，以及电流对电压的微分项dI_dV
V = 10.0
I = 2.0
dI_dV = -0.1

dP_dV = I + V * dI_dV
G = I / V
dG_dV = dI_dV / V - I / (V ** 2)

if dP_dV > 0:
    if dG_dV > 0:
        print("向电压增大方向调整工作点")
    else:
        print("向电压减小方向调整工作点")
else:
    if dG_dV > 0:
        print("向电压减小方向调整工作点")
    else:
        print("向电压增大方向调整工作点")

在这段代码里，先计算出$\frac{dP}{dV}$和$\frac{dG}{dV}$ ，然后依据它们的正负来判断该朝哪个方向调整光伏电池的工作点，以便靠近最大功率点。

变步长电导增量法

传统的电导增量法在跟踪速度和精度之间存在一定矛盾。固定步长下，大步长跟踪速度快，但容易在最大功率点附近振荡，降低精度；小步长虽然精度高，但跟踪速度慢。变步长电导增量法就很好地解决了这个问题。

它采用三段式寻优控制。在远离最大功率点时，采用大步长快速接近；靠近最大功率点时，逐渐减小步长，提高跟踪精度；在最大功率点附近，采用极小步长，减少振荡。

下面用Matlab代码展示一下变步长电导增量法的大致实现（以Matlab 2022a版本为例，Matlab 2018b版本代码基本一致，部分函数可能存在兼容性差异）：

% 初始化参数
V = 0; % 初始电压
I = 0; % 初始电流
step_size1 = 0.5; % 大步长
step_size2 = 0.1; % 中步长
step_size3 = 0.01; % 小步长
P_old = 0;
while true
    P = V * I;
    dP = P - P_old;
    dV = V - V_old;
    G = I / V;
    dG = (I - I_old) / V - I / (V * V) * dV;
    if abs(dP / dV) > 0.5 % 远离最大功率点
        V = V + step_size1 * sign(dP / dV);
    elseif abs(dP / dV) > 0.1 % 靠近最大功率点
        V = V + step_size2 * sign(dP / dV);
    else % 最大功率点附近
        V = V + step_size3 * sign(dP / dV);
    end
    % 更新电流、旧功率和旧电压
    I = get_current(V); % 假设这个函数能根据电压获取当前电流
    P_old = P;
    V_old = V;
    % 判断是否满足停止条件，这里简单假设功率变化小于某个阈值就停止
    if abs(dP) < 0.01
        break;
    end
end

在这段Matlab代码里，通过判断 $\frac{dP}{dV}$ 的大小来决定采用哪种步长调整电压$V$ 。远离最大功率点时，$\frac{dP}{dV}$绝对值较大，使用大步长$step\size1$快速调整；随着逐渐靠近最大功率点，$\frac{dP}{dV}$绝对值变小，改用中步长$step\size2$ ；在最大功率点附近，$\frac{dP}{dV}$接近0，采用小步长$step\_size3$ ，有效减少振荡，提高跟踪精度。

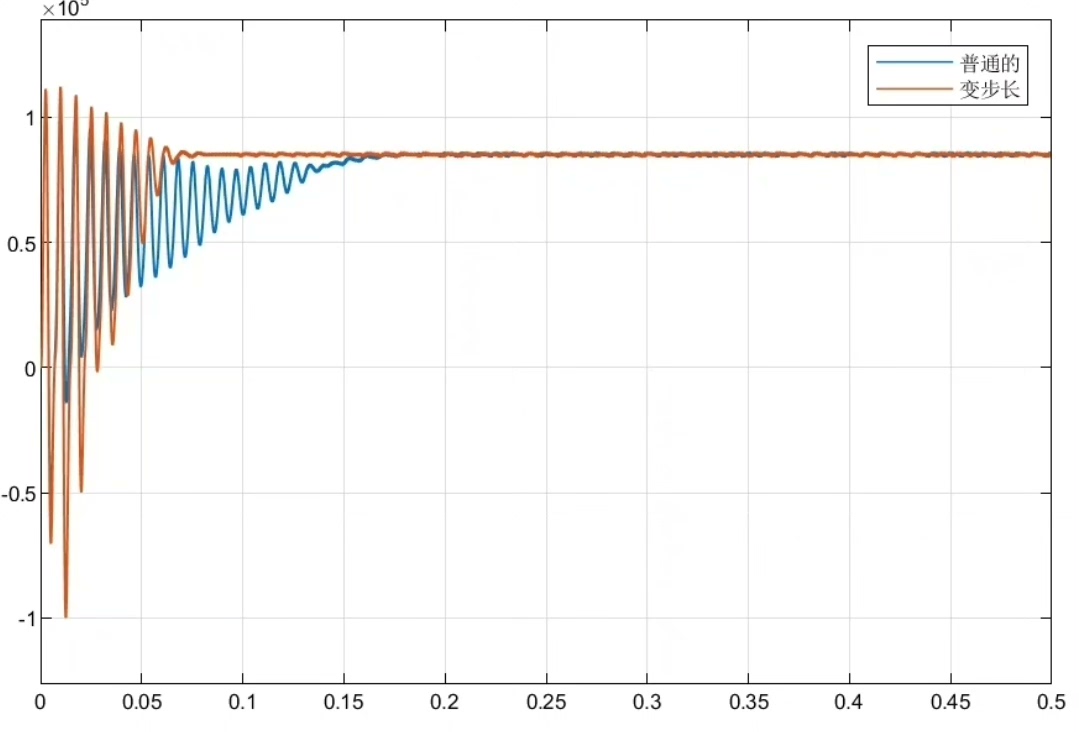
跟踪效果

实际应用中，变步长电导增量法的跟踪效果相当不错。相比传统固定步长的电导增量法，它能更快地跟踪到最大功率点，并且在最大功率点附近的振荡明显减小。无论是光照强度快速变化，还是温度等环境因素波动，三段式寻优控制的变步长电导增量法都能展现出良好的适应性，让光伏系统稳定高效地运行。

对应的Word设计报告与文件版本

如果大家想要深入了解变步长电导增量法的设计细节、理论分析以及完整的系统架构等内容，可以参考对应的Word设计报告。目前该报告有Matlab 2022a和2018b两种文件版本。Matlab 2022a版本在代码函数调用和绘图等方面可能会有一些新特性，而2018b版本则更适合一些配置稍旧的环境。大家可以根据自己的实际情况选择相应版本的文件进行参考和学习。

希望通过这篇博文，能让大家对光伏MPPT中的变步长电导增量法有更清晰的认识和理解，在实际项目中更好地应用这一技术。