时间序列初阶

1. 时间序列的定义：

例如：序列集合,是按照时间t1，……tn大小顺序排序得到的。

2. 时间序列的分类：

时间序列分为：平稳时间序列和非平稳时间序列。

平稳时间序列又分为宽平稳与严平稳。（我们见到的往往是宽平稳）

平稳时间序列：是围绕某一数值进行上下波动，且无明显的趋势性，

非平稳时间序列：一般指时间序列中包含其他的成分，如趋势性，周期性，季节性以及不规则性等。

对于不平稳的时间序列一般进行差分处理。(差分的阶数视情况而定）

检验平稳性的方法有（DF，ADF,PP等等）

ADF检验最为常用，在ADF检验中假设变量服从AR（P),其特征方程为，若所有的特征根均在单位圆内（即各特征根均小于1），则表明该序列是平稳序列，因此构建假设检验：

H0:, H1： 即原假设H0为该序列不平稳

其中：

在ADF检验中主要有三种形式：

①既含有常数均值项，又含有趋势项，AR（P）表达式：

（其中i从1开始）

②既不含有常数均值项，也不含趋势项，AR(P)表达式：

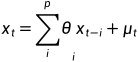
③含有常数均值项，不含有趋势项，AR（P)表达式：

选择哪一种可根据散点图判断：

例如：

上图很显然具有趋势，则其具有趋势项，上面三种只有①符合要求。

ADF检验的顺序一般是：

原始数据->一阶差分->二阶差分（不在进行2阶以上差分，因为2阶以上经济意义缺失）

检验的形式一般是先检验最复杂的情形，即

含常数项和趋势项->含常数项->无（类似于求导，一次变常数，常数消失）

其它选项默认就好。

例如：

上图可知p值大于0.05，无法拒绝原假设，即该序列为不平稳序列。

下面进行一阶差分：

继续进行2阶差分：

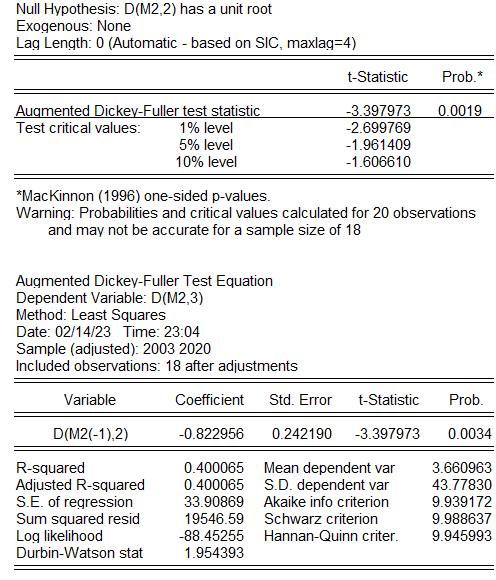
此时p值小于0.05，则说明二阶差分后的数据平稳。（注意经济意义）

自相关和偏自相关

ACF自相关：考虑中间过程

k为时间间隔

PACF偏自相关：只考虑两个点

简单理解为：去除了中间部分的影响。比如要求1和5的相关性，要把2.3.4的影响剔除掉，只是单纯看两个点的相关性。

例如：

若图为：

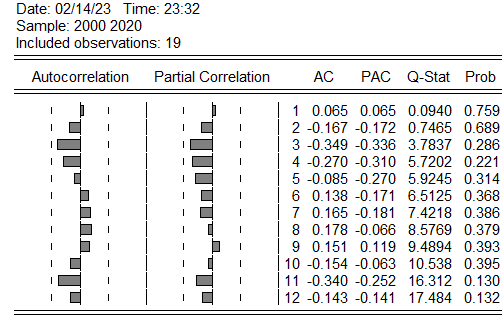
由于数据在2阶差分后才为平稳数据，所以ACF,PACF应用2阶差分数据

图中AC为自相关系数，PAC为偏自相关系数，虚线为2倍标准差。

图中均位于2倍标准差内，所以为白噪声序列。

若图为

图中一些位于2倍标准差内，一些位于2倍标准差之外，可用于后面判断，同时p值小于0.05，说明自相关性和偏自相关性强。