BP Neural Network

Back Propagation neural work

BP神经网络是前馈型网络，所处理信息逐层向前流动， 当学习时，根据期望输出与实际输出的误差，由前向后逐层修改权值。神经网络原理可对变量进行贡献分析，进而剔除影响不显著和不重要的因素，以简化模型。人工神经网络具有高度的并行结构和并行实现能力，因而其总体处理能力较快。

BP neural network 采用梯度（非线性规划）下降法使权值的改变总是朝着误差变小的方向，最后达到最小误差。它采用非线性规划中的最速下降方法，按误差函数的负梯度方向修改权值。

当前主要应用领域：模式识别，故障检测，智能机器人，非线性系统辨识和控制，市场分析，决策优化，物资调用，智能接口，知识处理，认知科学。

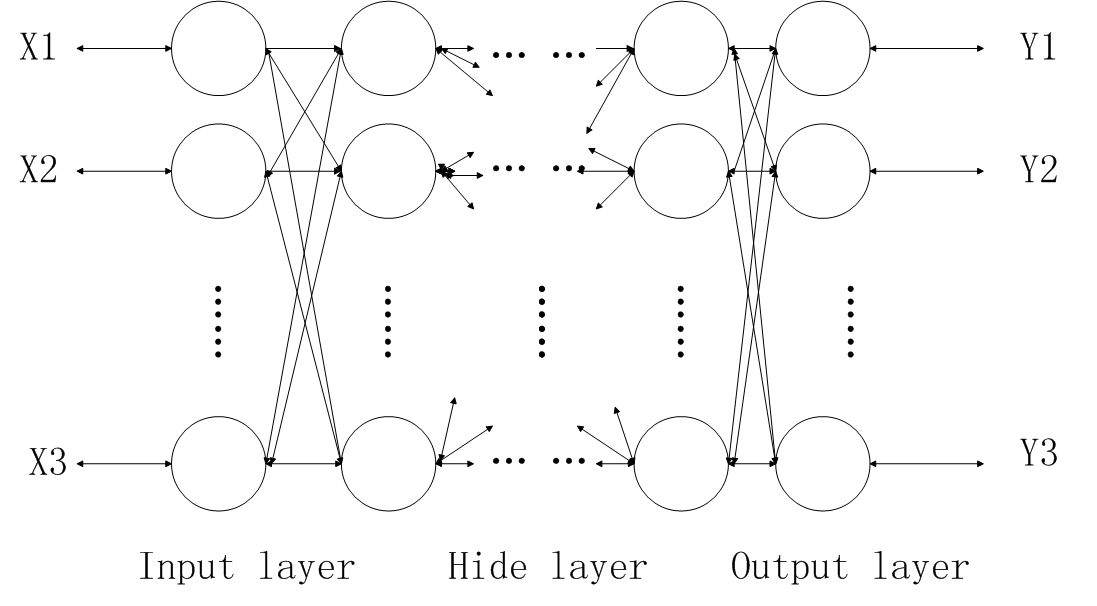
神经网络结构图

BP算法在于利用输出层的误差来估计输出层的直接前导层的误差，再利用此误差估计更前一层的误差，如此循环就获得了所有其他各层的误差估计。以此形成将输出端表现出的误差沿着与输入信号传送相反的方向逐级向网络的输入端传递的过程。

BP算法是一个迭代算法，由输入数据正向传播和误差方向传播两个子过程组成。

1. 工作信号正向传播：输入信号从输入层静隐含层，传向输出层，输出端产生输出信号，信号向前传递过程中网络权值固定不变，每一层神经元的状态只影响到下一层神经元的状态，若输出层得不到期望输出，则误差信号反向传播。
2. 误差信号反向传播：网络实际输出与期望输出之间的差值即为误差信号，误差由输出端逐层向前传播，网络的权值由误差反馈进行调节，通过不断修正权值是网络实际输出更接近期望输出。

插播：
- 在BP神经网络里，传递函数要求必须可微。
- 神经网络里所使用的函数必须是激活函数，激活函数是指如何把“激活的神经元的特征”通过函数把特征保留并影射出来（保特征，去冗余）。
- 激活函数用来加入非线性因素，毕竟线性模型表达力不够。

训练步骤：

该训练中，我们以一个三层的BP神经网络为例，来做训练描述。
关于所有变量，做如下假设：
网络输入向量：$P_k=(a_1,a_2,...,a_n)$
网络目标向量：$T_k=(y_1,y_2,...,y_q)$
中间层单元输入向量：$S_k=(s_1,s_2,...,s_p)$，输出向量$B_k=(b_1,b_2,...,b_p)$
输出层单元输出向量：$L_k=(l_1,l_2,...,l_q)$，输出向量$C_k=(c_1,c_2,...,c_q)$
输出层至中间层的连接权：${w_i}_j$，$i=1,2,...n,j=1,2,...p$
中间层至输出层的连接权：${v_j}_t$， j=1