我们知道Fibonacci数列,现在我们来求一个Fib数模n的循环节的长度。
对于一个正整数n,我们求Fib数模n的循环节的长度的方法如下:
(1)把n素因子分解,即
(2)分别计算Fib数模每个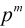
(3)那么Fib模n的循环节长度
从上面三个步骤看来,貌似最困难的是第二步,那么我们如何求Fib模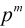
这里有一个优美的定理:Fib数模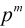
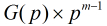
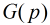
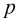
对于求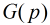
如果5是模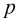
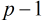
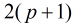
顺便说一句,对于小于等于5的素数,我们直接特殊判断,loop(2)=3,loop(3)=8,loop(5)=20。
那么我们可以先求出所有的因子,然后用矩阵快速幂来一个一个判断,这样时间复杂度不会很大。
模板代码:
#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>
#include <math.h>
using namespace std;
typedef unsigned long long LL;
const int M = 2;
struct Matrix
{
LL m[M][M];
};
Matrix A;
Matrix I = {1,0,0,1};
Matrix multi(Matrix a,Matrix b,LL MOD)
{
Matrix c;
for(int i=0; i<M; i++)
{
for(int j=0; j<M; j++)
{
c.m[i][j] = 0;
for(int k=0; k<M; k++)
c.m[i][j] = (c.m[i][j]%MOD + (a.m[i][k]%MOD)*(b.m[k][j]%MOD)%MOD)%MOD;
c.m[i][j] %= MOD;
}
}
return c;
}
Matrix power(Matrix a,LL k,LL MOD)
{
Matrix ans = I,p = a;
while(k)
{
if(k & 1)
{
ans = multi(ans,p,MOD);
k--;
}
k >>= 1;
p = multi(p,p,MOD);
}
return ans;
}
LL gcd(LL a,LL b)
{
return b? gcd(b,a%b):a;
}
const int N = 400005;
const int NN = 5005;
LL num[NN],pri[NN];
LL fac[NN];
int cnt,c;
bool prime[N];
int p[N];
int k;
void isprime()
{
k = 0;
memset(prime,true,sizeof(prime));
for(int i=2; i<N; i++)
{
if(prime[i])
{
p[k++] = i;
for(int j=i+i; j<N; j+=i)
prime[j] = false;
}
}
}
LL quick_mod(LL a,LL b,LL m)
{
LL ans = 1;
a %= m;
while(b)
{
if(b & 1)
{
ans = ans * a % m;
b--;
}
b >>= 1;
a = a * a % m;
}
return ans;
}
LL legendre(LL a,LL p)
{
if(quick_mod(a,(p-1)>>1,p)==1) return 1;
else return -1;
}
void Solve(LL n,LL pri[],LL num[])
{
cnt = 0;
LL t = (LL)sqrt(1.0*n);
for(int i=0; p[i]<=t; i++)
{
if(n%p[i]==0)
{
int a = 0;
pri[cnt] = p[i];
while(n%p[i]==0)
{
a++;
n /= p[i];
}
num[cnt] = a;
cnt++;
}
}
if(n > 1)
{
pri[cnt] = n;
num[cnt] = 1;
cnt++;
}
}
void Work(LL n)
{
c = 0;
LL t = (LL)sqrt(1.0*n);
for(int i=1; i<=t; i++)
{
if(n % i == 0)
{
if(i * i == n) fac[c++] = i;
else
{
fac[c++] = i;
fac[c++] = n / i;
}
}
}
}
LL find_loop(LL n)
{
Solve(n,pri,num);
LL ans=1;
for(int i=0; i<cnt; i++)
{
LL record=1;
if(pri[i]==2)
record=3;
else if(pri[i]==3)
record=8;
else if(pri[i]==5)
record=20;
else
{
if(legendre(5,pri[i])==1)
Work(pri[i]-1);
else
Work(2*(pri[i]+1));
sort(fac,fac+c);
for(int k=0; k<c; k++)
{
Matrix a = power(A,fac[k]-1,pri[i]);
LL x = (a.m[0][0]%pri[i]+a.m[0][1]%pri[i])%pri[i];
LL y = (a.m[1][0]%pri[i]+a.m[1][1]%pri[i])%pri[i];
if(x==1 && y==0)
{
record = fac[k];
break;
}
}
}
for(int k=1; k<num[i]; k++)
record *= pri[i];
ans = ans/gcd(ans,record)*record;
}
return ans;
}
void Init()
{
A.m[0][0] = 1;
A.m[0][1] = 1;
A.m[1][0] = 1;
A.m[1][1] = 0;
}
int main()
{
LL n;
Init();
isprime();
while(cin>>n)
cout<<find_loop(n)<<endl;
return 0;
}
典型题目
题目一:http://acm.hdu.edu.cn/showproblem.php?pid=3977
题目二:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=5075
题目三:http://acm.hdu.edu.cn/showproblem.php?pid=3978
题目四:http://acm.hdu.edu.cn/showproblem.php?pid=4291
上面的题目一和题目二基本上是模板题,没有什么可以说的。对于第三题和第四题,我们可以看出题目四实际上是
题目三的简单版,都是一层一层找循环节,我们找出每一层的循环节后即可解决。
下面给出题目三的代码:
#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>
#include <math.h>
using namespace std;
typedef long long LL;
const int M=2;
struct Matrix
{
LL m[M][M];
};
Matrix per= {1,0,0,1};
Matrix multi(Matrix a,Matrix b,LL MOD)
{
Matrix c;
int i,j,k;
for(i=0; i<M; i++)
{
for(j=0; j<M; j++)
{
c.m[i][j]=0;
for(k=0; k<M; k++)
{
c.m[i][j]+=a.m[i][k]*b.m[k][j]%MOD;
}
c.m[i][j]%=MOD;
}
}
return c;
}
Matrix power(Matrix a,LL k,LL MOD)
{
Matrix ans=per,p=a;
while(k)
{
if(k&1)
{
ans=multi(ans,p,MOD);
k--;
}
k>>=1;
p=multi(p,p,MOD);
}
return ans;
}
LL gcd(LL a,LL b)
{
return b? gcd(b,a%b):a;
}
LL quick_mod(LL a,LL b,LL m)
{
LL ans=1;
a%=m;
while(b)
{
if(b&1)
{
ans=ans*a%m;
b--;
}
b>>=1;
a=a*a%m;
}
return ans;
}
//勒让德符号
int legendre(int a,int p)
{
if(quick_mod(a,(p-1)>>1,p)==1) return 1;
else return -1;
}
const int N=1000005;
const int NN=50005;
bool prime[N];
int p[N];
int num[NN],pri[NN];
int num1[NN],pri1[NN];
int arr[NN];
int loop[N];
int k,cnt,c;
void isprime()
{
k=0;
int i,j;
memset(prime,true,sizeof(prime));
for(i=2; i<N; i++)
{
if(prime[i])
{
p[k++]=i;
for(j=i+i; j<N; j+=i)
{
prime[j]=false;
}
}
}
}
void find(int n,int pri[],int num[])
{
cnt=0;
int t=(int)sqrt(1.0*n);
for(int i=0; p[i]<=t; i++)
{
if(n%p[i]==0)
{
int a=0;
pri[cnt]=p[i];
while(n%p[i]==0)
{
a++;
n/=p[i];
}
num[cnt]=a;
cnt++;
}
}
if(n>1)
{
pri[cnt]=n;
num[cnt]=1;
cnt++;
}
}
void dfs(int dept,int product=1)
{
if(dept==cnt)
{
arr[c++]=product;
return;
}
for(int i=0; i<=num1[dept]; i++)
{
dfs(dept+1,product);
product*=pri1[dept];
}
}
int find_loop(int n)
{
find(n,pri,num);
int cnt1=cnt;
LL ans=1;
for(int i=0; i<cnt1; i++)
{
c=0;
int record=1;
if(pri[i]==2)
record=3;
else if(pri[i]==3)
record=8;
else if(pri[i]==5)
record=20;
else
{
if(legendre(5,pri[i])==1)
find(pri[i]-1,pri1,num1);
else
find(2*(pri[i]+1),pri1,num1);
dfs(0,1);
sort(arr,arr+c);
for(int k=0; k<c; k++)
{
Matrix A;
A.m[0][0]=1;
A.m[0][1]=1;
A.m[1][0]=1;
A.m[1][1]=0;
Matrix a=power(A,arr[k]-1,pri[i]);
int x=(a.m[0][0]+a.m[0][1])%pri[i];
int y=(a.m[1][0]+a.m[1][1])%pri[i];
if(x==1&&y==0)
{
record=arr[k];
break;
}
}
}
for(int k=1; k<num[i]; k++)
record*=pri[i];
ans=ans/gcd(ans,record)*record;
}
return ans;
}
void Solve(int p,int k)
{
loop[0]=p;
for(int i=1; i<=k; i++)
loop[i]=find_loop(loop[i-1]);
}
int work(int n,int k,int p)
{
int t=n;
LL ret,MOD;
Matrix ans;
Matrix A;
A.m[0][0]=1;
A.m[0][1]=1;
A.m[1][0]=1;
A.m[1][1]=0;
Solve(p,k);
for(int i=k; i>=0; i--)
{
MOD=loop[i];
ans=power(A,t,MOD);
ret=(ans.m[1][0]+ans.m[1][1])%MOD;
t=ret;
}
return ret;
}
int main()
{
isprime();
int T,n,k,p,tt=1;
scanf("%d",&T);
while(T--)
{
scanf("%d%d%d",&n,&k,&p);
printf("Case #%d: %d\n",tt++,work(n,k,p));
}
return 0;
}
题目:http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1195
分析:由于本题数据特别多,开始一直TLE,后来发现矩阵乘法里面如果取模太多会导致速度变得很慢,以前POJ上
的一道题关于矩阵求和也是因为这个TLE,尽量减少一些取模,速度会有几十倍甚至几百倍的提升。
代码:
#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>
#include <math.h>
#include <map>
using namespace std;
typedef long long LL;
const int M = 2;
struct Matrix
{
LL m[M][M];
};
Matrix A;
Matrix I = {1,0,0,1};
Matrix multi(Matrix a,Matrix b,LL MOD)
{
Matrix c;
for(int i=0; i<M; i++)
{
for(int j=0; j<M; j++)
{
c.m[i][j] = 0;
for(int k=0; k<M; k++)
c.m[i][j] += a.m[i][k] * b.m[k][j];
c.m[i][j] %= MOD;
}
}
return c;
}
Matrix power(Matrix a,LL k,LL MOD)
{
Matrix ans = I,p = a;
while(k)
{
if(k & 1)
{
ans = multi(ans,p,MOD);
k--;
}
k >>= 1;
p = multi(p,p,MOD);
}
return ans;
}
int gcd(int a,int b)
{
return b? gcd(b,a%b):a;
}
const int N = 400005;
const int NN = 5005;
int num[NN],pri[NN];
int fac[NN];
bool flag[NN];
int c;
bool prime[N];
int p[N];
int k;
int cnt1;
int pri1[NN],num1[NN];
void isprime()
{
k = 0;
memset(prime,true,sizeof(prime));
for(int i=2; i<N; i++)
{
if(prime[i])
{
p[k++] = i;
for(int j=i+i; j<N; j+=i)
prime[j] = false;
}
}
}
LL quick_mod(LL a,LL b,LL m)
{
LL ans = 1;
a %= m;
while(b)
{
if(b & 1)
{
ans = ans * a % m;
b--;
}
b >>= 1;
a = a * a % m;
}
return ans;
}
int legendre(int a,int p)
{
if(quick_mod(a,(p-1)>>1,p)==1) return 1;
else return -1;
}
void Solve(int n,int pri[],int num[],int &cnt)
{
cnt = 0;
int t = (int)sqrt(1.0*n);
for(int i=0; p[i]<=t; i++)
{
if(n%p[i]==0)
{
int a = 0;
pri[cnt] = p[i];
while(n%p[i]==0)
{
a++;
n /= p[i];
}
num[cnt] = a;
cnt++;
}
}
if(n > 1)
{
pri[cnt] = n;
num[cnt] = 1;
cnt++;
}
}
void dfs(int dept,int cnt,LL product,int pri1[],int num1[])
{
if(dept == cnt)
{
fac[c++] = product;
return;
}
for(int i=0; i<=num1[dept]; i++)
{
dfs(dept+1,cnt,product,pri1,num1);
product *= pri1[dept];
}
}
map<int,int> mp;
LL find_loop(LL n)
{
int cnt = 0;
Solve(n,pri,num,cnt);
LL ans = 1;
for(int i=0; i<cnt; i++)
{
int record=1;
if(mp.find(pri[i]) != mp.end())
{
record = mp[pri[i]];
goto Test;
}
if(pri[i]==2)
record=3;
else if(pri[i]==3)
record=8;
else if(pri[i]==5)
record=20;
else
{
if(legendre(5,pri[i])==1)
{
c = 0;
Solve(pri[i]-1,pri1,num1,cnt1);
dfs(0,cnt1,1,pri1,num1);
}
else
{
c = 0;
Solve(2*(pri[i]+1),pri1,num1,cnt1);
dfs(0,cnt1,1,pri1,num1);
}
sort(fac,fac+c);
for(int r=0; r<c; r++)
flag[r] = 1;
for(int k=c-1; k >= 0; k--)
{
if(!flag[k]) continue;
Matrix a = power(A,fac[k]-1,pri[i]);
int x = (a.m[0][0]%pri[i]+a.m[0][1]%pri[i])%pri[i];
int y = (a.m[1][0]%pri[i]+a.m[1][1]%pri[i])%pri[i];
if(x==1 && y==0)
{
record = fac[k];
}
else
{
for(int j=0; j<=k; j++)
{
if(fac[k] % fac[j] == 0)
flag[j] = 0;
}
}
}
mp[pri[i]] = record;
}
Test:
for(int k=1; k<num[i]; k++)
record *= pri[i];
ans=ans/gcd(ans,record)*record;
}
return ans;
}
void Init()
{
A.m[0][0] = 1;
A.m[0][1] = 1;
A.m[1][0] = 1;
A.m[1][1] = 0;
}
int main()
{
int T,n;
Init();
mp.clear();
isprime();
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
LL ans = find_loop(n);
printf("%I64d\n",ans);
}
return 0;
}








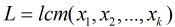
















 2325
2325

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








