题目:确定最小的正整数n,使得n!的结尾恰好有1987个0。
分析:我们首先来认识一个结论
设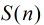
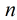
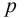
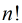
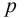

那么现在来证明这个结论:
设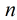
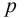
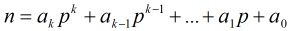
则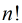
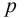
这样,题目就有了思路。我们知道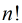
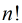
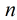
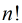
那么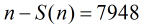
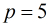
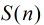
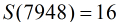
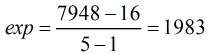
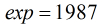
题目:确定最小的正整数n,使得n!的结尾恰好有1987个0。
分析:我们首先来认识一个结论
设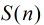
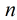
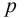
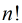
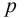

那么现在来证明这个结论:
设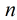
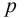
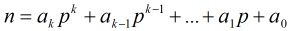
则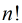
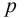
这样,题目就有了思路。我们知道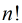
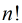
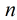
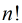
那么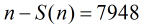
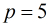
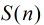
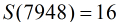
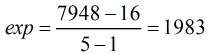
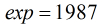
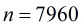

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


