对于一个线性递推式,求它第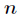

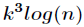
其实,由于这个矩阵的特殊性,可以将时间优化到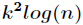
题目:http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1229
题意:设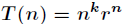
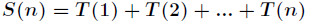
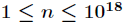
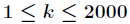
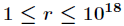
前言:本题如果用普通的矩阵做法,很明显会TLE。那么我们要对这个特殊的矩阵进行时间上的优化。
分析:本题主要可用两种方法解决,分别是错位相减和矩阵乘法。先来说说错位相减的基本做法,把题目描述改一下
以
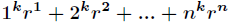
进而得到
接下来,我们重点关注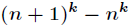
对于组合系数相同的进行合并得到
那么可以看出
这是一个递归式,递归出口是当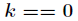
对于上述递归式,为了提高效率,需要进行记忆化,当然这里是针对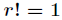
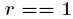
此时的问题就是典型的自然数幂和问题,关于自然数幂和问题的详细讲解,链接如下
自然数幂和:http://blog.csdn.net/acdreamers/article/details/38929067
代码:
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
typedef long long LL;
const int N = 2005;
const LL MOD = 1000000007;
LL n, r;
LL C[N][N];
LL B[N],Inv[N];
LL Tmp[N];
LL ans[N];
void Init()
{
//预处理组合数
for(int i=0; i<N; i++)
{
C[i][0] = C[i][i] = 1;
if(i == 0) continue;
for(int j=1; j<i; j++)
C[i][j] = (C[i-1][j] % MOD + C[i-1][j-1] % MOD) % MOD;
}
//预处理逆元
Inv[1] = 1;
for(int i=2; i<N; i++)
Inv[i] = (MOD - MOD / i) * Inv[MOD % i] % MOD;
//预处理伯努利数
B[0] = 1;
for(int i=1; i<N; i++)
{
LL ans = 0;
if(i == N - 1) break;
for(int j=0; j<i; j++)
{
ans += C[i+1][j] * B[j];
ans %= MOD;
}
ans *= -Inv[i+1];
ans = (ans % MOD + MOD) % MOD;
B[i] = ans;
}
}
LL quick_mod(LL a, LL b, LL m)
{
LL ans = 1;
a %= m;
while(b)
{
if(b & 1)
{
ans = ans * a % m;
b--;
}
b >>= 1;
a = a * a % m;
}
return ans;
}
LL Work1(int k)
{
LL ans = Inv[k+1];
LL sum = 0;
for(int i=1; i<=k+1; i++)
{
sum += C[k+1][i] * Tmp[i] % MOD * B[k+1-i] % MOD;
sum %= MOD;
}
ans *= sum;
ans %= MOD;
return ans;
}
LL Work2(int k)
{
if(ans[k] != -1) return ans[k];
if(k == 0)
{
ans[k] = r * (quick_mod(r, n, MOD) - 1) % MOD * quick_mod(r-1, MOD-2, MOD) % MOD;
ans[k] = (ans[k] % MOD + MOD) % MOD;
return ans[k];
}
ans[k] = quick_mod(n+1, k, MOD) * quick_mod(r, n+1, MOD) % MOD * quick_mod(r-1, MOD-2, MOD) % MOD;
LL tmp = r * quick_mod(r-1, MOD-2, MOD) % MOD;
LL sum = 1;
for(int i=k-1; i>=0; i--)
{
sum += C[k][k-i] * Work2(i);
sum %= MOD;
}
ans[k] -= sum * tmp % MOD;
ans[k] = (ans[k] % MOD + MOD) % MOD;
return ans[k];
}
int main()
{
int T;
Init();
scanf("%d", &T);
while(T--)
{
int k;
memset(ans, -1, sizeof(ans));
scanf("%I64d %d %I64d", &n, &k, &r);
r %= MOD;
if(r == 1)
{
n %= MOD;
Tmp[0] = 1;
for(int i=1; i<N; i++)
Tmp[i] = Tmp[i-1] * (n + 1) % MOD;
LL ret = Work1(k);
printf("%I64d\n", ret);
continue;
}
LL ans = Work2(k);
printf("%I64d\n", ans);
}
return 0;
}
已经很完美地解决了上述题目,其实还有一个矩阵乘法的做法,这才是我们今天要讨论的重点。以前在HDU上就做过一道与本题差不多的题目,链接是:http://acm.hdu.edu.cn/showproblem.php?pid=3483
几乎跟本题差不多,但是HDU3483的数据比较小,普通的矩阵乘法完全没有压力,但是同样的方法却不能用在此处。
因为本题的
杂度大大降低。接下来,我会用构造矩阵的方法来详细解析本题。设
将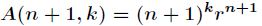
那么可以构造如下递推矩阵
接下来,可以通过上面的递推矩阵在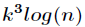
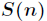
--上三角矩阵,可以将时间优化到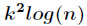
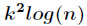
先来介绍一个很重要的定理----Cayley-Hamilton定理,描述如下
设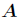
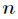
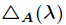
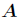
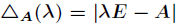

用一句话概括就是:方阵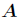
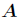
更多关于Cayley-Hamilton定理的学习请戳这里。
本题主要参考这篇文章:《线性递推关系与矩阵乘法》,如下
主要用到本文的如下内容









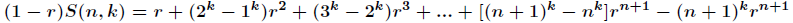
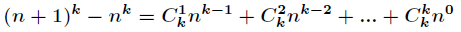
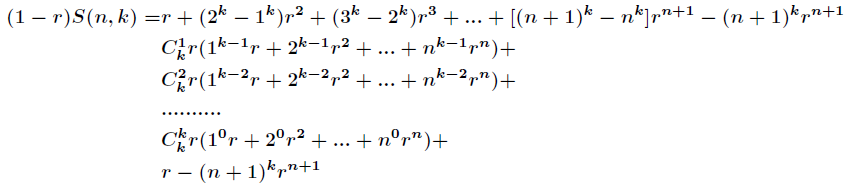
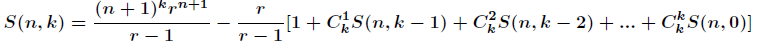
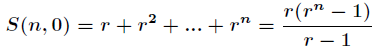
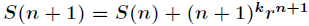
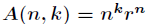
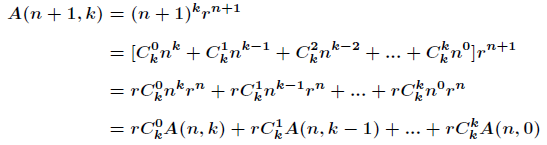
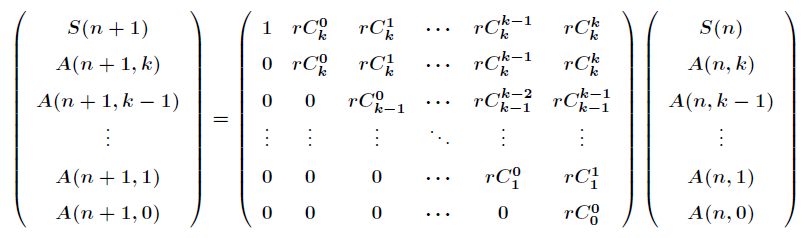

















 323
323

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








