前言
合抱之木,生于毫末;九层之台,起于垒土;千里之行,始于足下。为者败之,执者失之。
一、矩阵的一些用途
矩阵乘法在处理线性运算,特别是递推式问题中,确实具有重大作用,并且在很多情况下可以显著加快运算速度。以下是一些关键点:
训练题中遇到了第一种用途,下面整理一下学习结果
线性递推式的矩阵表示:
很多线性递推式可以表示为矩阵的幂的形式。例如,斐波那契数列的第n项可以通过一个2x2的矩阵的n-1次幂来高效计算。这种表示方法使得我们可以利用矩阵乘法的性质来优化计算。快速矩阵乘法算法:
传统的矩阵乘法算法的时间复杂度是O(n^3),其中n是矩阵的维度。但是,存在一些更高效的算法,如Strassen算法和Coppersmith-Winograd算法,它们可以在某些情况下实现更低的复杂度。尽管这些算法在实际应用中并不常见(因为它们的常数因子很大),但它们证明了矩阵乘法问题在理论上的可优化性。矩阵快速幂:
由于矩阵乘法满足结合律,我们可以使用类似于整数快速幂的算法来计算矩阵的幂。具体来说,我们可以将指数表示为二进制形式,并只计算必要的矩阵乘法,从而避免重复计算。这种算法的时间复杂度通常是O(log n),其中n是指数。线性变换和状态转移:
在动态规划、图论、线性变换等问题中,矩阵乘法经常用于表示状态转移。通过将问题建模为状态转移矩阵,我们可以利用矩阵乘法的性质来优化计算。并行计算和GPU加速:
矩阵乘法是一种高度可并行的计算任务,因此可以很容易地利用多核处理器或图形处理单元(GPU)进行加速。这种并行性使得矩阵乘法在处理大规模线性运算时具有特别的优势。
二、线性递推式的矩阵表示
1.以斐波那契数列的优化为例
1.递归法:
int f(int x )
{
if(x == 0) return 0 ;
if(x == 1 ) return 1 ;
return f(x - 1 ) + f(x - 2 ) ;
}2.记忆化搜索:
全局变量int fit[N] ;
int f(int x)
{
if(x == 0 ) return 0 ;
if(x == 1 ) return 1 ;
if(fit[x]) return fit[x];
return f[x] = f(x-1) + f(x-2) ;
}由此算法时间复杂度可以优化到O(n)𝑂(𝑛),但显然这种做法是以空间换时间,需要耗费相对较大的空间复杂度O(n)𝑂(𝑛)。虽然时间复杂度已经优化到线性,但面对较大的数据仍然略显吃力。
3.递推式矩阵加速
对于 f[n] = f[n-1] + f[n - 2 ] 对 f[n] 有用的是f[n-1] 和 f[n - 2 ] 。
我们可以有这样的一个想法
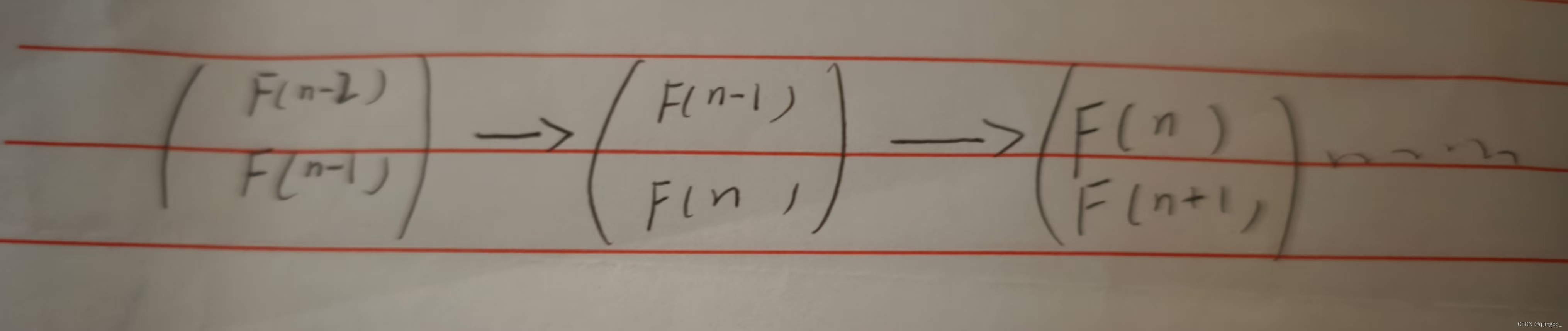
这样递推
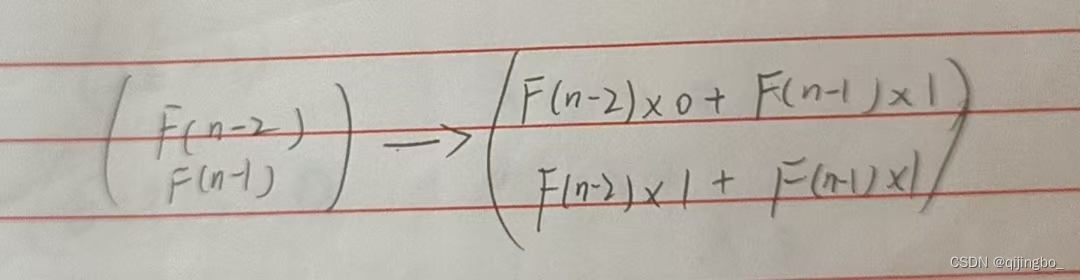
因为是二阶矩阵所以是(n-2)次方,或者随便找几个数往里试。
这里运用了矩阵快速幂,模板看我另一篇文章矩阵快速幂(模板)-CSDN博客
代码如下
#include<bits/stdc++.h>
using namespace std ;
const int mod = 1e9 + 7 ;
typedef long long LL ;
int t , n , k ;
struct matrix
{
LL c[5][5] ;
matrix(){memset(c,0,sizeof c) ;}
};
matrix operator *(const matrix&x , const matrix&y)
{
matrix t ;
for(int i = 1 ; i <= 2 ; i ++ )
{
for(int j = 1 ; j <= 2 ; j ++ )
{
for(int k = 1 ; k <= 2 ; k ++ )
{
t.c[i][j] = (t.c[i][j] + x.c[i][k] * y.c[k][j]) % mod ;
}
}
}
return t ;
}//定义矩阵相乘
void quickpow(matrix A )
{
matrix res ; //单位矩阵相当于普通快速幂模板的1
for(int i = 1 ; i <= 2 ; i ++) res.c[i][i] = 1 ;
while(k)
{
if(k&1) res = res * A;
A = A * A ;
k >>= 1 ;
}
LL ans = 0 ;
for(int i = 1 ; i <= 2 ; i ++ )
{
ans =(ans + res.c[2][i] )%mod;
}
cout << ans <<endl ;
}
void solve()
{
cin >> n ;
if(n > 0 &&n <= 2 ) cout << 1 <<endl ;
else{
k = n - 2 ;
matrix A ; //要进行幂运算的矩阵
A.c[1][2] = 1 , A.c[2][1] = 1 , A.c[2][2] = 1 ;
quickpow(A);
}
}
int main()
{
ios::sync_with_stdio(false) ;
cin.tie(0);
cout.tie(0);
cin >> t ;
while(t -- )
{
solve();
}
return 0 ;
}在quickpow这个函数里ans所做的操作为幂矩阵的最后一行元素与初始矩阵的列向量组相乘并连加,因为f1=1,f2=1,所以最后一行元素与1相乘还是本身,所以就直接加上自身就可以了
2.递推式有间隔的式子
洛谷P1939 矩阵加速(数列)
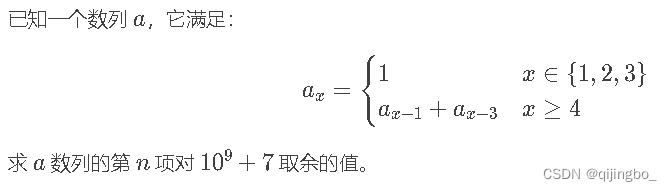
x-1 与x - 3 之间间隔 x-2 没有用到, 那这时候的矩阵递推式该怎么写,写成吗,可以动手试一试,发现要是写成这种二阶矩阵是组成不了递推式的,因为是递推式子,将f(n-2)写上去让式子往下递推即
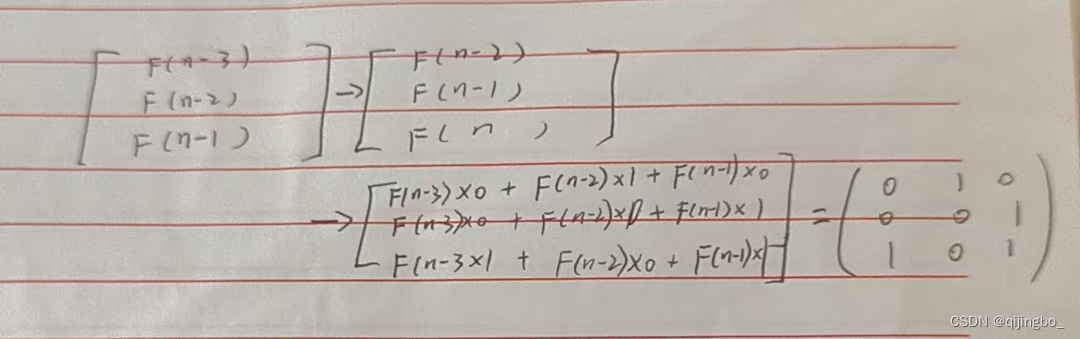
所以总结公式就是左乘图上矩阵的(n-3)次方再乘初等矩阵;
在这里我总结出来了规律就是
1.如果是x阶矩阵就乘(n - x ) 次方
2.左乘的矩阵一定是方阵,列与所乘的行相同,而答案所得的行数取决于自身,所以列与行都等于递推矩阵中的元素个数
代码如下
#include<bits/stdc++.h>
using namespace std ;
const int mod = 1e9 + 7 ;
typedef long long LL ;
int t , n , k ;
struct matrix
{
LL c[5][5] ;
matrix(){memset(c,0,sizeof c) ;}
};
matrix operator *(const matrix&x , const matrix&y)
{
matrix t ;
for(int i = 1 ; i <= 3 ; i ++ )
{
for(int j = 1 ; j <= 3 ; j ++ )
{
for(int k = 1 ; k <= 3 ; k ++ )
{
t.c[i][j] = (t.c[i][j] + x.c[i][k] * y.c[k][j]) % mod ;
}
}
}
return t ;
}
void quickpow(matrix A )
{
matrix res ;
for(int i = 1 ; i <= 3 ; i ++) res.c[i][i] = 1 ;
while(k)
{
if(k&1) res = res * A;
A = A * A ;
k >>= 1 ;
}
/*
for(int i = 1 ; i <= 3 ; i ++ )
{
for(int j = 1 ; j <= 3 ; j ++ )
{
cout << res.c[i][j] <<" " ;
}
cout << endl;
}
*/
//cout << endl ;
LL ans = 0 ;
for(int i = 1 ; i <= 3 ; i ++ )
{
ans =(ans + res.c[3][i] )%mod;
}
cout << ans <<endl ;
}
void solve()
{
cin >> n ;
if(n <= 3 ) cout << 1 <<endl ;
else{
k = n - 3 ;
//cout << k <<endl ;
matrix A ;
A.c[1][2] = 1 , A.c[2][3] = 1 , A.c[3][1] = 1 , A.c[3][3] = 1 ;
quickpow(A);
}
}
int main()
{
ios::sync_with_stdio(false) ;
cin.tie(0);
cout.tie(0);
cin >> t ;
while(t -- )
{
solve();
}
return 0 ;
}我这里对A的矩阵挨个赋值有点麻烦可以在结构体里加上
matrix(int a , int b , int c , int d , int e ,int f , int r,int t , int y )
{
c[1][1] = a , c[1][2] = b , c[1][3] = c ;
c[2][1] = d , c[2][2] = e , c[2][3] = f ;
c[3][1] = r, c[3][2] = t , c[3][3] = y ;
}
这样直接matrix A = matrix(0,1,0,0,0,1,1,0,1);







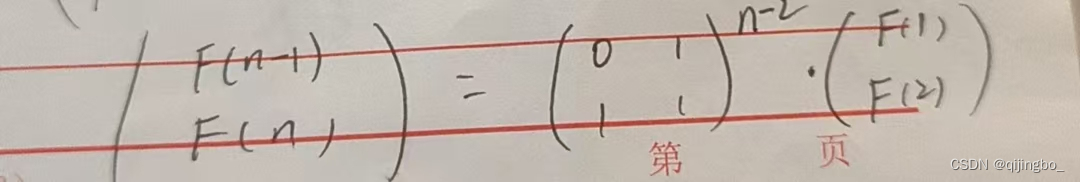














 305
305











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








