相关系数-简单描述

一、相关系数

又称皮尔逊相关系数，是研究变量之间相关关系的度量

二、计算方式

一般用字母r表示

两种计算公式

（1）

Cov(X,Y)为X与Y的协方差

Var[X]为X的方差

Var[Y]为Y的方差

（2）

总体皮尔逊相关系数是一个在【-1,1】之间波动变化的数值。
绝对值接近1说明变量之间具有明显的线性关系，接近0则说明变量之间几乎不存在相关关系。

三、相关系数的解释

1.|r| >= 0.8时，可视为两个变量之间高度相关

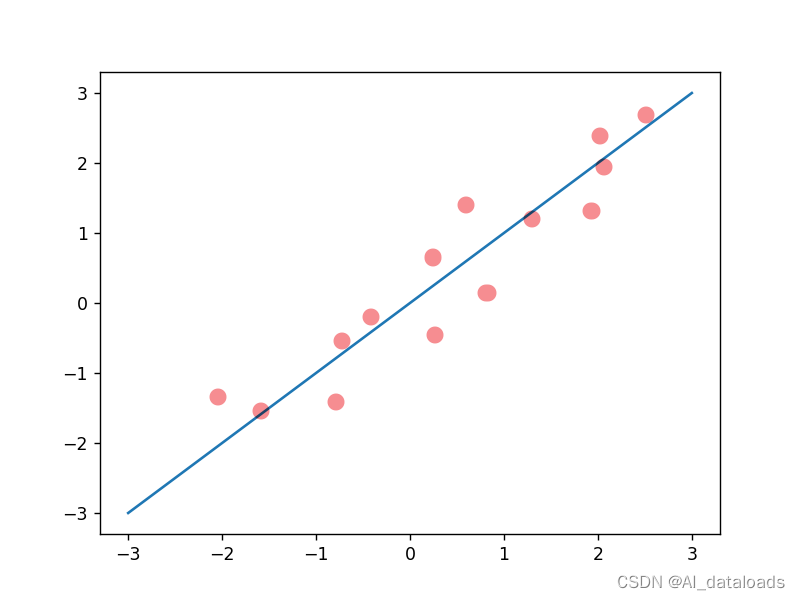
如图：数据与预测函数非常接近，甚至个别点落在线上，我们成为强相关。

2.|r| < 3 时，说明两个变量之间的相关系数程度极弱，可视为不相关

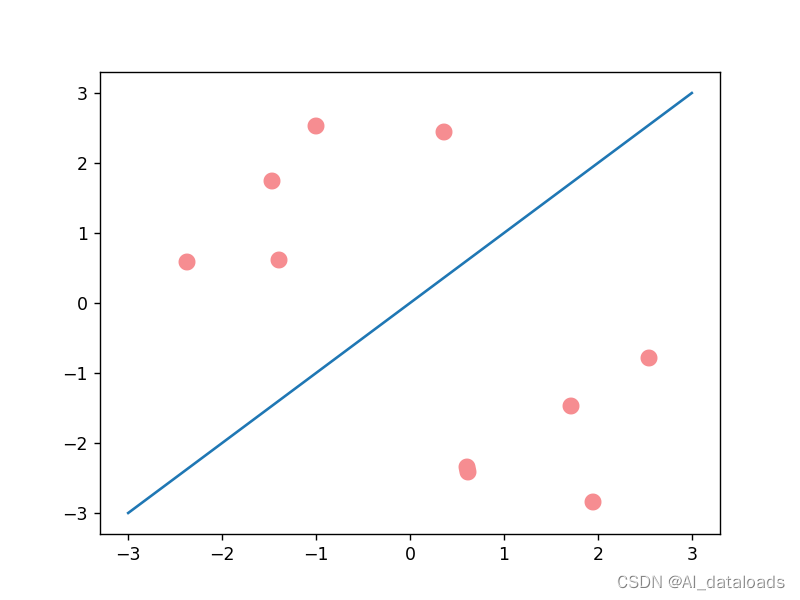
如图，样本点与预测函数相差较大，我们成为弱相关

除了强相关与弱相关，还有中度相关以及低度相关
3.0.5 <= |r| < 0.8时，可视为中度相关
4.0.3 <= |r| < 0.5时，可视为低度相关

四、示例

# 首先要从sklearn库中调取相应的包（注意：要从pip下载sklearn，要输入完整名scikit-learn）
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
# data为获取的上面图中的信息
x = data[['广告投入']]
y = data[['销售额']]
# 将数据进行训练
lr.fit(x, y)
# 将数据代入进去，进行预测，得到预测标签，并与真实数据标签进行比对，得到正确率，即相关系数
score = lr.score(x, y)

将广告投入与销售额进行相关系数计算
算的相关系数为0.8225，说明广告投入与销售额之间有高度的线性正相关关系。