目录
PCA降维是一种常用的数据分析方法,它通过将高维数据映射到低维空间来表示主成分分析的主要特征分量。这种方法的目标是在所投影的维度上使数据的方差最大,同时尽量使新的特征互不相关。
pca推导详见pca降维的推导
一、数据预处理
步骤1:将原始数据按列组成n行m列矩阵X:
例如:

步骤2:对X矩阵每一行进行零均值化:
也就是减去这一行的均值

第一行均值:(1+1+2+4+2)/ 5 = 2
每一个数据以此减去均值,得到零均值化数据(-1,-1,0,2,0)
第二行均值:(1+3+3+4+4)/ 5 = 3
每一个数据以此减去均值,得到零均值化数据(-2,0,0,1,1)
二、求协方差矩阵及其特征值和特征向量
求协方差矩阵
公式:
: 矩阵
:X矩阵的转置
: 特征数量
前面得到去均值化的X矩阵,利用公式,求得协方差矩阵
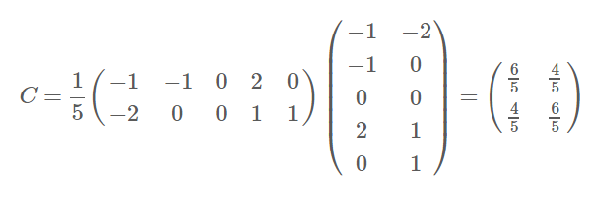
特征值和特征向量:
特征值:
利用公式计算特征值

E :二维单位矩阵
主对角线减去次对角线等于0即可求得特征值
这里将结果乘以5,对结果不影响
特征向量:
将λ1和λ2分别带入 𝝀𝑬 − C =0即可。


三、将特征向量组成矩阵P并对其进行对角化验证
p矩阵:
对角化验证:

四、数据降维
Y=PX即为降维到k维后的数据。
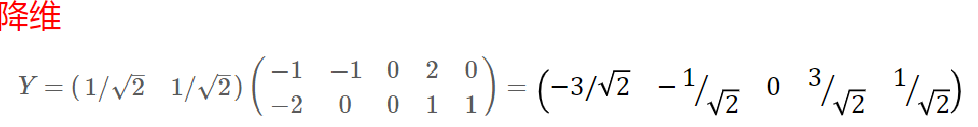
五、PCA优缺点
优点:
1.计算方法简单,容易实现。
2可以减少指标筛选的工作量。
3消除变量间的多重共线性。
4在一定程度上能减少噪声数据。
缺点:
1.特征必须是连续型变量。
2无法解释降维后的数据是什么。
3贡献率小的成分有可能更重要。







 本文详细介绍了PCA方法,包括数据预处理(零均值化),求协方差矩阵及其特征值向量,构建P矩阵并验证对角化,以及数据降维的过程。同时讨论了PCA的优点如简单实现和减少噪声,以及缺点如只适用于连续变量和信息解释性不足。
本文详细介绍了PCA方法,包括数据预处理(零均值化),求协方差矩阵及其特征值向量,构建P矩阵并验证对角化,以及数据降维的过程。同时讨论了PCA的优点如简单实现和减少噪声,以及缺点如只适用于连续变量和信息解释性不足。
















 1294
1294

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








