【泰勒综合平面阵的电流分布与阵因子方向图MATLAB仿真】

阵列天线的综合问题是其分析的逆问题，即是在预先给定辐射特性(如方向图形状、主瓣宽度、副瓣电平、方向性系数)的情况下，综合出阵列单元数、间距、激励幅度和相位。阵列天线的综合就是阵列天线的设计问题。

道尔夫-切比雪夫综合法

道尔夫-切比雪夫综合法是一种可控制副瓣电平的阵列天线综合方法，适合单元数目N≤13的阵列，具有以下特点：
(1) 等副瓣电平；
(2) 在相同副瓣电平和相同阵列长度下主瓣最窄，为最佳阵列；
(3) 单元数多时，阵列两端单元激励幅度跳变大，使馈电困难。

其阵因子函数为：
当单元数目为奇数即N=2M+1时，阵因子为：

当单元数目为偶数即N=2M时，阵因子为：

泰勒综合法

采用泰勒综合法设计的泰勒阵列，其方向图只是靠近主瓣某个区域内的副瓣电平接近相等，随后单调地减小，有利于提高天线方向性，适合单元数目N＞13的阵列。

均匀线阵方向图

其方向图函数为：

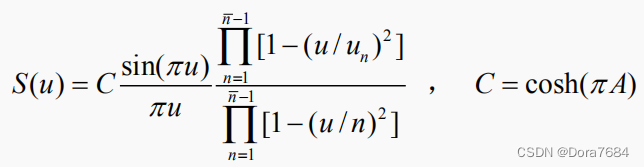
该函数的含义是：把基本函数的前n −1个零点用改造的理想空间因子的零点取代，而第n 个以后的零点保持为基本函数的零点。
其中，零点位置为：

理想空间因子：

当 u=0 为最大值时，

均匀线阵电流分布幅度

则离散化后泰勒阵列各单元的电流分布幅度可表示为：

式中：

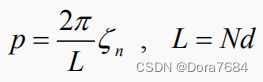
泰勒分布平面阵

矩形栅格的矩形平面阵列，如果其馈电分布是可分离型的，则该平面阵列的阵因子方向图就是沿 x 和 y 方向排列的直线阵列阵因子方向图的乘积。

其电流分布幅度为：

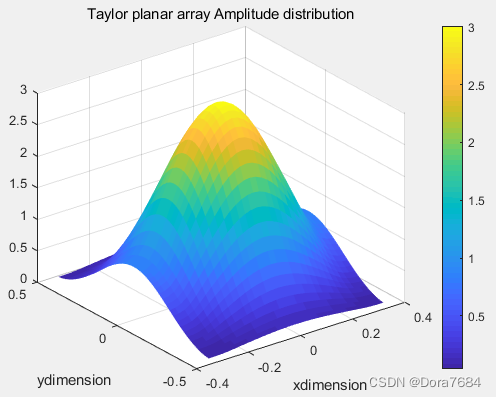
阵因子方向图为：

源代码：https://download.csdn.net/download/ALiTing_/86912120