【数学建模】matlab微分方程求解导弹追击问题（小白版）

记录学习微分方程时遇到的“拦路虎”，如有不足请斧正。

一、导弹追击问题

二、问题建模

简而言之，一导弹一船。导弹从(0,0)出发，船从(20,0)出发。导弹的方向朝船，速度为3v；船的方向为东北，速度为v。v为常数。导弹的射程是50个单位（描述距离）。欲求：导弹能否在射程内击中船？

以正东为x轴正方向，正北为y轴正方向
首先定义导弹所在点M的坐标($x(t)$,$y(t)$)，船N坐标($P(t),Q(t)$)，表示两点的位置随时间$t$变化而变
以下公式用$x,y,P,Q$代替$x(t),y(t),P(t),Q(t)$

通过导弹的速度分解，得到第一个等式：$$(\frac{\mathrm{d}x}{\mathrm{d}t}{)}^2+(\frac{\mathrm{d}y}{\mathrm{d}t}{)}^2=(3v{)}^2\text{\hspace{1em}(1)}$$
由于导弹的方向朝船，即导弹M速度方向朝N，即，$$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{Q-y}{P-x}\text{\hspace{1em}(2)}$$
因为$x,y$都是$t$的函数，上式转为下式，并赋值常数$\lambda$
$$\frac{\frac{\mathrm{d}y}{\mathrm{d}t}}{\frac{\mathrm{d}x}{\mathrm{d}t}}=\frac{Q-y}{P-x}=\lambda$$
因此，$\frac{\mathrm{d}x}{\mathrm{d}t},\frac{\mathrm{d}y}{\mathrm{d}t}$可表示为
$$\{\begin{array}{l}\frac{\mathrm{d}x}{\mathrm{d}t}=\lambda (P-x)\\ \frac{\mathrm{d}y}{\mathrm{d}t}=\lambda (Q-y)\end{array}\text{\hspace{1em}(3)}$$

目标是在方程中消去未知参数$\lambda$并优化公式(3)，因此联立(1)(3)，得$${\lambda }^2[(P-x{)}^2+(Q-y{)}^2]=9v^2$$
故，$$\lambda =\frac{3v}{\sqrt{(P-x{)}^2+(Q-y{)}^2}}\text{\hspace{1em}(4)}$$
因为$\lambda$在公式(2)中出现，此处代入获得$\frac{\mathrm{d}x}{\mathrm{d}t},\frac{\mathrm{d}y}{\mathrm{d}t}$的matlab中标准微分方程 形式
$$\{\begin{array}{l}\frac{\mathrm{d}x}{\mathrm{d}t}=\frac{3v}{\sqrt{(P-x{)}^2+(Q-y{)}^2}}\times (P-x)\\ \frac{\mathrm{d}y}{\mathrm{d}t}=\frac{3v}{\sqrt{(P-x{)}^2+(Q-y{)}^2}}\times (Q-y)\end{array}\text{\hspace{1em}(5)}$$
之后，对船的$x,y$轴速度进行数学描述（合速度大小$v$，方向东北，即和x轴夹角为45度），则有：
$$\{\begin{array}{l}\frac{\mathrm{d}P}{\mathrm{d}t}=v\times cos(45^{º})\\ \frac{\mathrm{d}Q}{\mathrm{d}t}=v\times sin(45^{º})\end{array}\text{\hspace{1em}(6)}$$
最终，$x,y,P,Q$的标准微分方程（5,6）建立完毕
同时，明确初始值： $x(0)=0,y(0)=0,P(0)=20,Q(0)=20$

三、matlab编程

1. 判断方程是否有解析解

使用dsolve(‘方程1’…‘方程n’,‘所有初始条件’,‘自变量’)，查看是否存在解析解。如果在，则能获得因变量$x,y,P,Q$表达式并直接画图。
这里偷懒使用了公式 (1)(2)作为方程1,2

%自变量't'该项可省，因dsolve默认自变量为t
dsolve('Dx^2+Dy^2=9*v^2','Dy/Dx=(q-y)/(p-x)','Dq = v/sqrt(2)','Dp = v/sqrt(2)','x(0)=0,y(0)=0,q(0)=0,p(0)=20','t')

按F9运行所选内容

不出所料，果然找不到解析解…然后标准形式的微分方程(5)(6)写入.m文件中找数值解，代码在第2部分。

2. matlab编程计算数值解

新建函数zztest.m。要注意的是使用求解函数求数值解时，函数头最好写成function dy = 函数名(自变量,因变量向量（通过列向量存储多变量）)
这里将参数传入，函数头改为function dy = 函数名(自变量,因变量向量（通过列向量存储多变量）,参数1,…,参数n)
但调用该函数求解时，需要用匿名函数修改

% 保存在zztest.m，和model.m在同一文件夹
function dy = zztest(t,y,v)
%导弹追击船
%   v是速度量
%   其实可以写在这个文件内，但因为是自定义参数所以从求解过程中分离
%   如
%   v = 1;

dy = zeros(4,1); %1,2是导弹的x,y，3，4是船的P,Q；最好用该方式表示多变量
dy(1) = 3*v/sqrt((y(3)-y(1))^2+(y(4)-y(2))^2)*(y(3)-y(1)); %左侧只能为导数dy形式，右侧不能出现导数
dy(2) = 3*v/sqrt((y(3)-y(1))^2+(y(4)-y(2))^2)*(y(4)-y(2));
dy(3) = v*cos(4/pi);
dy(4) = v*sin(4/pi);
end

在另一个脚本文件（model.m，和test.m在同一文件夹）中使用求解器函数，首先实验ode45。求解器函数的普通格式solver(‘微分方程文件’,‘自变量范围’,‘因变量的初始值’)
这里通过匿名函数限制自变量为t、因变量y（和test.m一致），分别设置$v=1,2,3$以求解数值解，因为求数值解的微分方程中不能出现未知参数。
同时，由于导弹路程最大$50$单位，速度大小恒为$3v$，则时间$t$最大为$\frac{50}{3v}$

% 保存在model.m，和zztest在同一文件夹
for v = 1:3
    [t1,y1] = ode45(@(t,y)zztest(t,y,v),[0,50/(3*v)],[0,0,20,0]);% [0,0,20,0]: 因为y是4行的列向量，所以初始值有4个
    
    % 画图
    subplot(1,3,v) %第1行第3列，第v个子图（v取1，2，3）
    plot(y1(:,1),y1(:,2),'r--',y1(:,3),y1(:,4),'b') % y为未知（行）*4的向量；r--红色虚线
    t = strcat('导弹追船 v=',num2str(v)); %字符串拼接
    title(t)
    legend('导弹路径','船路径','Location','Best') %Location:调整图例位置，这里设Best
end

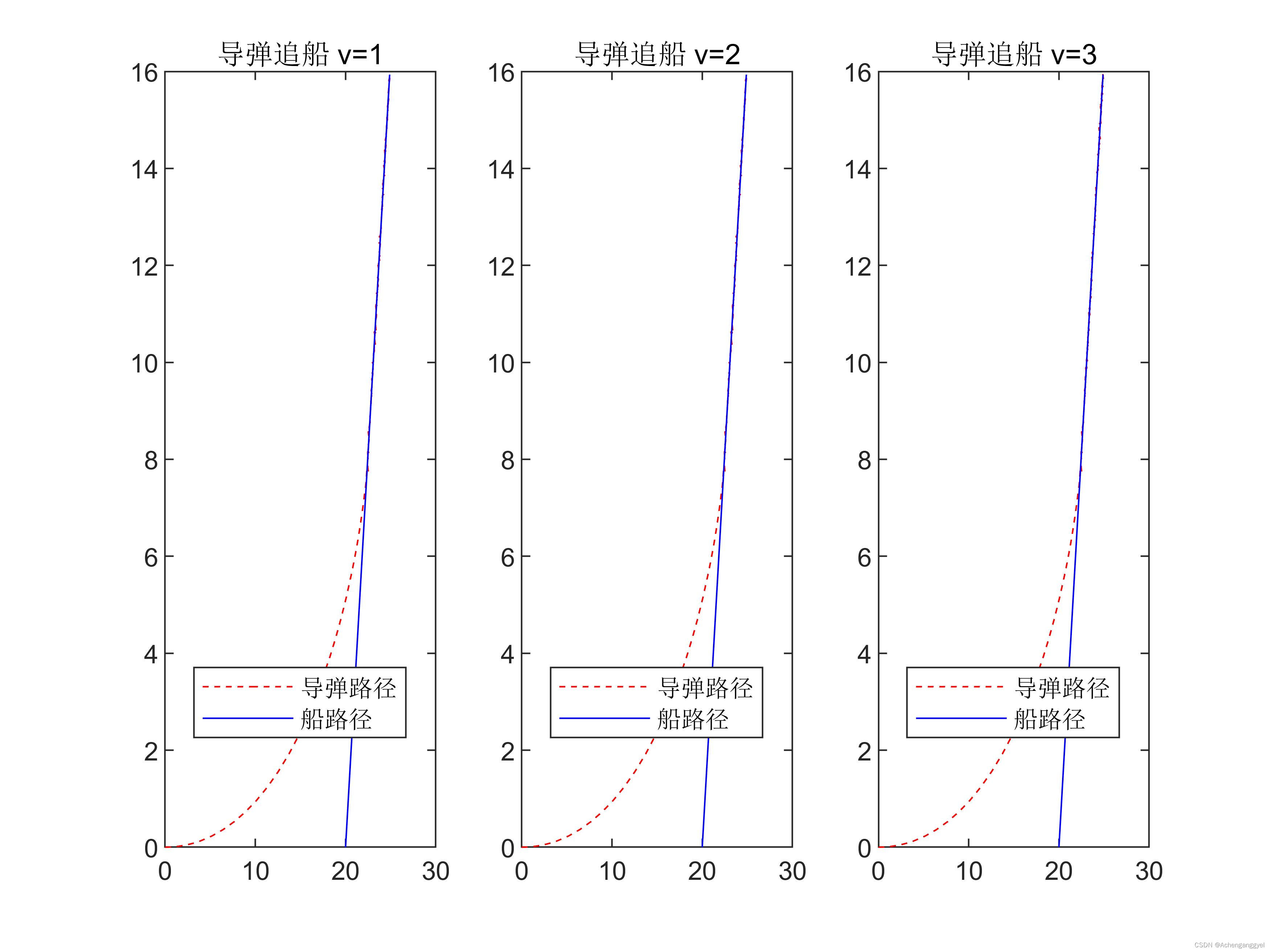
路径图如下
发现无论$v$取何值，路径图都不改变。由于限制条件是导弹的路程小于50个单位，即$\sqrt{(x^2+y^2)}<=50$，可以认为$v$的取值不影响问题的求解。因此设$v=3$

最后展示下$v$在微分方程文件中赋值的写法
zztest_2t.m

% 微分方程过程
% 保存在zztest_2.m，和model.m在同一文件夹
function dy = zztest_2(t,y)
%导弹追击船
v = 1; % v是速度量

dy = zeros(4,1); %1,2是导弹的x,y，3，4是船的P,Q；最好用该方式表示多变量
dy(1) = 3*v/sqrt((y(3)-y(1))^2+(y(4)-y(2))^2)*(y(3)-y(1)); %左侧只能为导数dy形式，右侧不能出现导数
dy(2) = 3*v/sqrt((y(3)-y(1))^2+(y(4)-y(2))^2)*(y(4)-y(2));
dy(3) = v*cos(4/pi);
dy(4) = v*sin(4/pi);
end

model.m

% 调用求解器函数求解微分方程
% 保存在model.m，和zztest_2.m在同一文件夹
[t2,y2] = ode45('zztest_2',[0,50/(3*v)],[0,0,20,0]);

另，这里踩了一个坑，就是实时脚本无法复制代码…建议先用脚本写，之后再转实时脚本查看；或对文件美观有要求、想要即时函数提示的，可以用实时脚本写代码

3. 探讨导弹和船是否相撞

尽管路径图表明，后续导弹M和船N的路径重合。但我们不清楚时间相同时，M、N是否在同一点相遇
所以，这里通过代码验证

%% 判断导弹和船是否相撞
% 用t1,y1来判断
n = length(y1(:,1)); % n是该情况所有matlab求解的数值解
error = 1e-2; % 容许误差；因数值解是近似解而非真实解
              %          误差太小会找不到，如1e-3就无输出
for i = 1:n
    % 用导弹和船的距离来判断
    d_MN= sqrt((y1(i,3)-y1(i,1)).^2+(y1(i,4)-y1(i,2)).^2);
    if d_MN < error
        words = ['时间: ',num2str(t1(i,1)), ' 位置x: ',num2str(y1(i,1)), ' 位置y: ', num2str(y1(i,2))];
        disp(words);
        break
    end
end

运行结果

故可知导弹将击中船，且在一定误差范围内，导弹飞行时间2.8008秒，于(22.4589,8.0323)位置击中。

4. 代码整合

所有代码如下，在同一文件夹下。
zztest.m

function dy = zztest(t,y,v)
%导弹追击船
%   v是速度量
%   其实可以写在这个文件内，但因为是自定义参数所以从求解过程中分离
%   如
%   v = 1;

dy = zeros(4,1); %1,2是导弹的x,y，3，4是船的P,Q；最好用该方式表示多变量
dy(1) = 3*v/sqrt((y(3)-y(1))^2+(y(4)-y(2))^2)*(y(3)-y(1)); %左侧只能为导数dy形式，右侧不能出现导数
dy(2) = 3*v/sqrt((y(3)-y(1))^2+(y(4)-y(2))^2)*(y(4)-y(2));
dy(3) = v*cos(4/pi);
dy(4) = v*sin(4/pi);
end

zztest_2.m

function dy = zztest_2(t,y)
%导弹追击船
v = 1; % v是速度量

dy = zeros(4,1); %1,2是导弹的x,y，3，4是船的P,Q；最好用该方式表示多变量
dy(1) = 3*v/sqrt((y(3)-y(1))^2+(y(4)-y(2))^2)*(y(3)-y(1)); %左侧只能为导数dy形式，右侧不能出现导数
dy(2) = 3*v/sqrt((y(3)-y(1))^2+(y(4)-y(2))^2)*(y(4)-y(2));
dy(3) = v*cos(4/pi);
dy(4) = v*sin(4/pi);
end

model.m

%% 导弹追踪船问题
% 求解函数（两种参数设定） + 判断是否追击成功
%% 微分方程传参
for v = 1:3
    [t1,y1] = ode45(@(t,y)zztest(t,y,v),[0,50/(3*v)],[0,0,20,0]);% [0,0,20,0]: 因为y是4行的列向量，所以初始值有4个
    
    % 画图
    subplot(1,3,v)
    plot(y1(:,1),y1(:,2),'r--',y1(:,3),y1(:,4),'b') % y为未知（行）*4的向量；r--红色虚线
    t = strcat('导弹追船 v=',num2str(v));
    title(t)
    legend('导弹路径','船路径','Location','Best') %Location:调整图例位置，这里设Best
end
%% 微分方程内部参数设置
[t2,y2] = ode45('zztest_2',[0,50/(3*v)],[0,0,20,0]);
%% 判断导弹和船是否相撞
% 用t1,y1来判断
n = length(y1(:,1)); % n是该情况所有matlab求解的数值解
error = 1e-2; % 容许误差；因数值解是近似解而非真实解
              %          误差太小会找不到，如1e-3就无输出
for i = 1:n
    % 用导弹和船的距离来判断
    d_MN= sqrt((y1(i,3)-y1(i,1)).^2+(y1(i,4)-y1(i,2)).^2);
    if d_MN < error
        words = ['相撞时间: ',num2str(t1(i,1)), ' 位置x: ',num2str(y1(i,1)), ' 位置y: ', num2str(y1(i,2))];
        disp(words);
        break
    end
end

四、一点废话

对于微分方程而言，难的不是求解，而是问题建模、方程化简、细节考虑。这么说是因为第一次画出图像的时候，发现和清风的大为不同…然后发现是微分方程的标准形式不规范
所以，这个建模问题，妙就妙在是道很简单的数学题，但本人却是才疏学浅、数学物理均堪忧的大学生（笑）