数据结构14.自平衡二叉查找树_AVL树

引言

　在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为一，所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O（log n）。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
　AVL树得名于它的发明者G.M. Adelson-Velsky和E.M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。

一． AVL树定义

平衡二叉树又称AVL树,它或者是一棵空树,或者是具有下列性质的二叉排序树:
- 它的左子树和右子树都是平衡二叉树,
- 且左子树和右子树高度之差的绝对值不超过1.

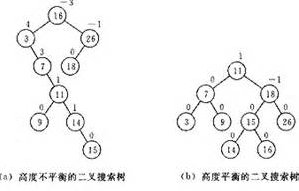
图给出了两棵二叉排序树,树中每个节点旁边所标记的数字是以该节点为根的二叉树的左子树和右子树的高度之差,该数字被称为节点的平衡因子.

由平衡二叉树的定义可知, 平衡二叉树中的所有节点的平衡因子只能取1、0或-1中的一个值。平衡因子的绝对值大于1,如带有 -2或2的节点被认为是不平衡的，并需要重新平衡这个树。平衡因子可以直接存储在每个节点中，或从可能存储在节点中的子树高度计算出来。
二叉排序树是一棵完全二叉树或者与折半查找的判定树相似时,其查找性能最好,而当二叉排序树蜕化为单支树时其查找性能最差.因此,二叉排序树最好是一棵平衡二叉树.
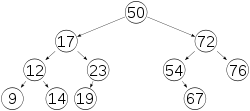
保持二叉排序树为平衡二叉树的基本思想是:每当给二叉排序树插入一个新节点时,就检查是否因为这次插入而破坏了平衡;如果破坏了平衡,则找出其中最小的不平衡树,在保持二叉排序树有序的前提下,调整最小不平衡树中节点的关系以达到新的平衡.所谓最小不平衡树即指距插入节点最近且其平衡因子的绝对值大于1的节点做根的这样一棵子树.

我们将平衡二叉树定义为:

typedef struct AVL_node{
    int                data;  //节点数据域
    int              height;  //节点高度
    struct AVL_node  * left;  //左孩子
    struct AVL_node  *right;  //右孩子
}AVL_node;                    //节点

typedef AVL_node *AVL_Tree;   //树

二．AVL树的接口

• avl_tree.h

#ifndef _AVL_TREE_H_
#define _AVL_TREE_H_

typedef struct AVL_node{
    int                data;  //节点数据域
    int              height;  //节点高度
    struct AVL_node  * left;  //左孩子
    struct AVL_node  *right;  //右孩子
}AVL_node;                    //节点

typedef AVL_node *AVL_Tree;   //树

#define  ONE       (1)
#define  max(a, b) ((a) < (b) ? (b) : (a))


//AVL树的接口
//1.        得到树的高度
int         get_tree_height(AVL_Tree root)             ;
//2.        遍历二叉树
//2.1       前序遍历
void        preorder_avltree(AVL_Tree root)            ;
//2.2       中序遍历
void        inorder_avltree(AVL_Tree root)             ;
//2.3       后序遍历
void        postorder_avltree(AVL_Tree root)           ;

//3.        查找数据域为value的节点
//3.1       递归查找
AVL_node *  find_node(AVL_Tree root, int value)        ; 
//3.2       非递归查找
AVL_node *  find_node_(AVL_Tree root, int value)       ; 
//3.3       找到值最大的节点
AVL_node *  get_max_node(AVL_Tree root)                ;
//3.4       找到值最小的节点
AVL_node *  get_min_node(AVL_Tree root)                ;

//4.        将节点插入到avl树中
AVL_Tree    avltree_insert(AVL_Tree root, int data)    ;    
//5.        从avl树中删除指定数值
AVL_Tree    avltree_delete(AVL_Tree root, int data)    ;
//6.        销毁avl树
void        destroy_avltree(AVL_Tree root)             ;
#endif//_AVL_TREE_H_

三. AVL树的接口实现

查找

可以像普通二叉查找树一样的进行，所以耗费O(log n)时间，因为AVL树总是保持平衡的。不需要特殊的准备，树的结构不会由于查找而改变。（这是与伸展树查找相对立的，它会因为查找而变更树结构。）

插入

AVL树的基本操作一般涉及运作同在不平衡的二叉查找树所运作的同样的算法。但是要进行预先或随后做一次或多次所谓的”AVL旋转”。

有四种种情况可能导致二叉查找树不平衡，分别为：

LL：插入一个新节点到根节点的左子树(Left)的左子树(Left),导致根节点的平衡因子由1变为2
RR：插入一个新节点到根节点的右子树(Right)的右子树(Right),导致根节点的平衡因子由-1变为-2
LR：插入一个新节点到根节点的左子树(Left)的右子树(Right),导致根节点的平衡因子由1变为2
RL：插入一个新节点到根节点的右子树(Righ)的左子树(Left),导致根节点的平衡因子由-1变为-2

针对四种种情况可能导致的不平衡，可以通过旋转使之变平衡。有两种基本的旋转：

左旋转：将根节点旋转到（根节点的）右孩子的左孩子位置
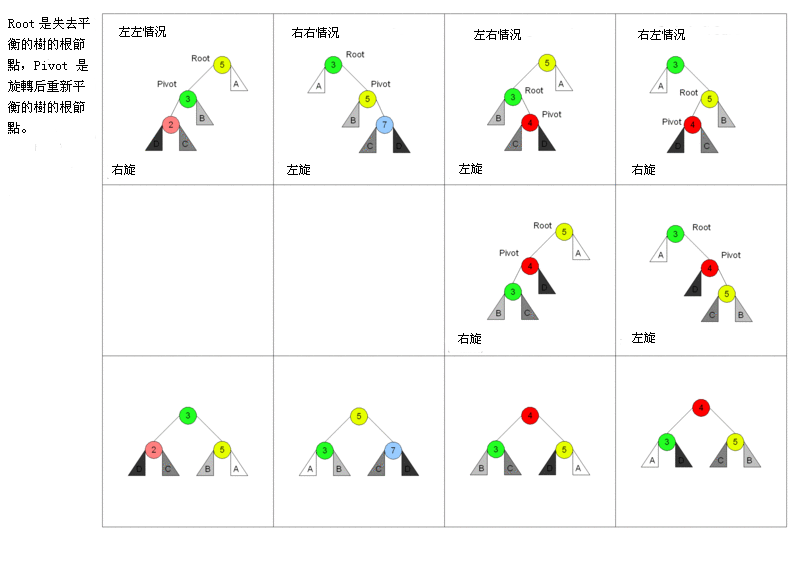
右旋转：将根节点旋转到（根节点的）左孩子的右孩子位置

以下图表以四列表示四种情况，每行表示在该种情况下要进行的操作。在左左和右右的情况下，只需要进行一次旋转操作；在左右和右左的情况下，需要进行两次旋转操作。

假设由于在二叉排序树上插入节点而失去平衡的最小子树根节点的指针为a（即a是离插入点最近，且平衡因子绝对值超过1的祖先节点），则失去平衡后进行的规律可归纳为下列四种情况：

单向右旋平衡处理LL：由于在*a的左子树根节点的左子树上插入节点，*a的平衡因子由1增至2，致使以*a为根的子树失去平衡，则需进行一次右旋转操作；

单向左旋平衡处理RR：由于在*a的右子树根节点的右子树上插入节点，*a的平衡因子由-1变为-2，致使以*a为根的子树失去平衡，则需进行一次左旋转操作；

双向旋转（先左后右）平衡处理LR：由于在*a的左子树根节点的右子树上插入节点，*a的平衡因子由1增至2，致使以*a为根的子树失去平衡，则需进行两次旋转（先左旋后右旋）操作。

双向旋转（先右后左）平衡处理RL：由于在*a的右子树根节点的左子树上插入节点，*a的平衡因子由-1变为-2，致使以*a为根的子树失去平衡，则需进行两次旋转（先右旋后左旋）操作。

• 删除
  从AVL树中删除节点node，可以分三种情况:

  1. node的左右子树其中一个为空,则将node指向node的非空孩子,然后释放掉node;
  2. node在左子树,则在左子树删除掉节点之后,检测不平衡状态,是否右边高于左边,然后根据右子树情况,判断是RR,还是RL,进行旋转.
  3. node在右子树,根据删除节点之后是否不平衡,根据左子树判断是否需要LL右旋,或是LR.
     或者:
     (从AVL树中删除，可以透过把要删除的节点向下旋转成一个葉子節點，接着直接移除这个叶子节点来完成。因为在旋转成葉子節點期间最多有log n个节点被旋转，而每次AVL旋转耗费固定的时间，所以删除处理在整体上耗费O(log n) 时间。)

• avl_tree.c

#include <stdio.h>
#include <stdlib.h>
#include <strings.h>
#include "tools.h"
#include "avl_tree.h"


//创建一个节点
static AVL_node *create_node(void)
{
    AVL_node *result = (AVL_node *)Malloc(sizeof(AVL_node));
    if(result == NULL)
    {
        fprintf(stderr, "the memory is full!\n");
        exit(1);
    }
    bzero(result, sizeof(AVL_node));
    return result;
}
//获取节点结构中的高度变量
static int node_height(AVL_Tree node)
{
    if(node == NULL)
    {
        return -1;
    }
    return node->height;
}
//计算节点的高度
static int avl_node_height(AVL_node *node)
{
    return max(node_height(node->left), node_height(node->right)) + 1;
}

//1.        得到树的高度
int      get_tree_height(AVL_Tree root)    //得到avl树的高度
{
    return node_height(root);
}

//2.        遍历二叉树
void     preorder_avltree(AVL_Tree root)    //2.1前序遍历avl树
{
    if(root != NULL)
    {
        printf("%d ", root->data);
        preorder_avltree(root->left);
        preorder_avltree(root->right);
    }
}

void     inorder_avltree(AVL_Tree root)     //2.2中序遍历avl树
{
    if(root != NULL)
    {
        inorder_avltree(root->left);
        printf("%d ", root->data);
        inorder_avltree(root->right);
    }
}

void     postorder_avltree(AVL_Tree root)   //2.3后序列遍历avl树
{
    if(root != NULL)
    {
        postorder_avltree(root->left);
        postorder_avltree(root->right);
        printf("%d ", root->data);
    }
}
//3.查找数据域为value的节点
//3.1.递归方式查找
AVL_node *find_node(AVL_Tree root, int value)
{
    if(root == NULL || root->data == value)
    {
        return root;
    }
    if(value < root->data)//小于,去左子树
    {
        return find_node(root->left, value);
    }
    else
    {
        return find_node(root->right, value);
    }
}
//3.2.非递归方式查找
AVL_node *find_node_(AVL_Tree root, int value)
{
    AVL_node *p_node = root;

    while(p_node != NULL)
    {
        if(p_node->data > value)//如果当前节点的值大于被查找的值，则继续比较当前节点的左孩子
        {
            p_node = p_node->left;
        }
        else if(p_node->data < value)//如果当前节点的值小于被查找的值，则继续比较当前节点的右孩子
        {
            p_node = p_node->right;
        }
        else//当前节点的值符合要求
        {
            return p_node;
        }
    }
    return NULL;
}
//3.3       找到值最大的节点
AVL_node *get_max_node(AVL_Tree root)    //找到值最大的节点
{
    AVL_node *p_node = root;

    while