西瓜书 4. 决策树

数学基础

1. 基本流程

• 一棵决策树包含 一个根结点、若干个内部结点和若干个叶结点
  • 叶结点对应于决策结果，其他每个结点则对应于一个属性测试
  • 每个结点包含的样本集合根据属性测试的结果被划分到子结点中
  • 根结点包含样本全集

• 第8行：每次选择一个属性作为划分依据，然后按属性的取值将数据集中的样本进行划分，划分完得到若干子集，接着再对各个子集按照以上流程重新选择某个属性继续递归划分

• 决策树的生成是一个递归过程，3个$return$代表递归返回，运行到$return$就停止划分

  • 行 2-4 ：若递归划分过程中某个子集中已经只含有某一类的样本(例如只含好瓜)，那么此时划分的目的已经达到了，无需再进行递归划分
  • 行 5-7 ：
    • 递归划分时每次选择一个属性作为划分依据，并且该属性通常不能重复使用(仅针对离散属性)，原因是划分后产生的各个子集在该属性上的取值相同。若所有属性均已被用作过划分依据，即 $A=\varnothing$，此时子集中仍含有不同类样本(例如仍然同时含有好瓜和坏瓜)，但是因已无属性可用作划分依据，此时只能少数服从多数，以此子集中样本数最多的类为标记。
    • 虽然 $A\ne \varnothing$，但是当子集中的样本在属性集合 $A$ 上取值都相同时，等价视为 $A=\varnothing$
  • 行 11-12：根据某个属性进行划分时，若该属性多个属性值中的某个属性值不包含任何样本(例如未收集到)，因为无样本落入，将其标记为叶结点，其类别标记为训练集 $D$ 中样本最多的类，即把全体样本的分布作为当前结点的先验分布。其实就是一种盲猜，既然是盲猜，那么合理的做法就是根据已有数据用频率近似概率的思想假设出现频率最高的便是概率最大的。注意，此分支必须保留，因为测试时，可能会有样本落入该分支。

2. 划分选择

1. 信息増益：ID3

• 信息熵：$Ent(D)=-\sum _{k=1}^{|\mathcal{Y}|}{p}_k{\log }_2{p}_k$
  • 其中：假定当前样本集合 $D$ 中第 $k$ 类样本所占的比例为 $p_k(p=1,2,...,|\mathcal{Y}|)$
  • 约定：若 $p=0$，则 $p{\log }_{2}p=0$
  • $0\le Ent(D)\le {\log }_2|\mathcal{Y}|$（证明见南瓜书）
  • $Ent(D)$ 的值越小，则 $D$ 的纯度越高
• 信息增益：$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)$
  • 其中：假定离散属性 $a$ 有 $V$ 个可能的取值 { a 1 , a 2 , . . . , a V } \{a^1,a^2,...,a^V\} {a1,a2,...,aV}
  • 若使用 $a$ 来对样本集 $D$ 进行划分，则会产生 $V$ 个分支结点，其中第 $v$ 个分支结点包含了 $D$ 中所有在属性 $a$ 上取值为 $a^v$ 的样本，记为 $D^v$
• ID3算法：算法第 8 行选择属性$a_{\ast }=\underset{a\in A}{\mathrm{argmax}}Gain(D,a)$

2. 增益率：C4.5

• 信息增益准则对可取值数目较多的属性有所偏好，为减少这种偏好可能带来的不利影响，C4.5 决策树算法使用“增益率” (gain ratio)来选择最优划分属性
• 增益率：$Gai{n}_{r}adio(D,a)=\frac{Gain(D,a)}{IV(a)}$
  • 其中：定义属性 $a$ 的固有值 $IV(a)=-\sum _{v=1}^V\frac{|D^v|}{|D|}{\log }_2\frac{|D^v|}{|D|}$
  • 属性 $a$ 的可能取值数目越多(即 $V$ 越大)，则 $IV(a)$ 的值通常会越大
• 增益率准则对可取值数目较少的属性有所偏好，因此，C4.5 算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式： 先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的

3. 基尼指数：CART

• 基尼值：$Gini(D)=\sum _{k=1}^{|\mathcal{Y}|}\sum _{k^{\prime }\ne k}{p}_k{p}_k^{\prime }=1-\sum _{k=1}^{|\mathcal{Y}|}{p}_k^2$
  • $Gini(D)$ 反映了从数据集 $D$ 中随机抽取两个样本，其类别标记不一致的概率。因此， $Gini(D)$ 越小，则数据集 $D$ 的纯度越高
• 属性 $a$ 的基尼指数定义：$Gini\_index(D,a)=\sum _{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)$
• $a_{\ast }=\underset{a\in A}{\mathrm{argmin}}Gain\_index(D,a)$
• 在构造 CART 决策树时，并不会严格按照此式来选择最优划分属性，主要是因为 CART 决策树是一棵二叉树，如果用上式去选出最优划分属性，无法进一步选出最优划 分属性的最优划分点。常用的 CART 决策树的构造算法如下：
  1. 考虑每个属性 $a$ 的每个可能取值 $v$，将数据集 $D$ 分为 $a=v$ 和 $a\ne v$ 两部分来计算基尼指数，即：$Gini\_index(D,a)=\frac{|D^{a=v}|}{|D|}Gini(D^{a=v})+\frac{|D^{a\ne v}|}{|D|}Gini(D^{a\ne v})$
  2. 选择基尼指数最小的属性及其对应取值作为最优划分属性和最优划分点
  3. 重复以上两步，直至满足停止条件
• CART 除了决策树能处理分类问题以外，回归树还可以处理回归问题，CART 回归树的
  构造算法见南瓜书

3. 剪枝处理

1. 预剪枝

• 预剪枝是指在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶结点
• 未剪枝決策树：
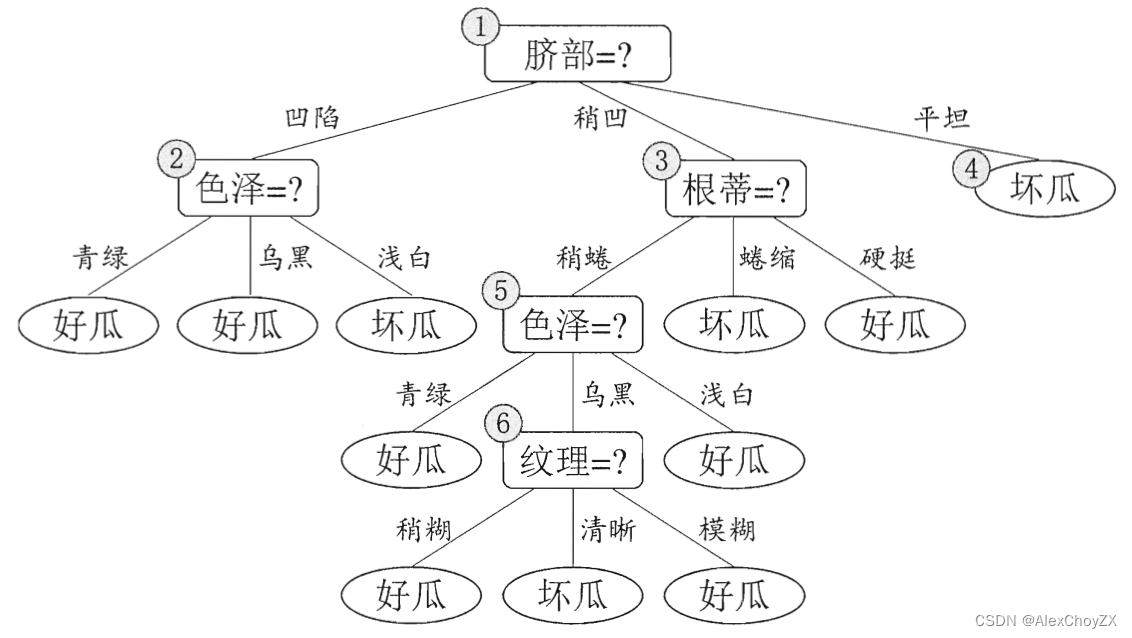
• 预剪枝决策树：
  
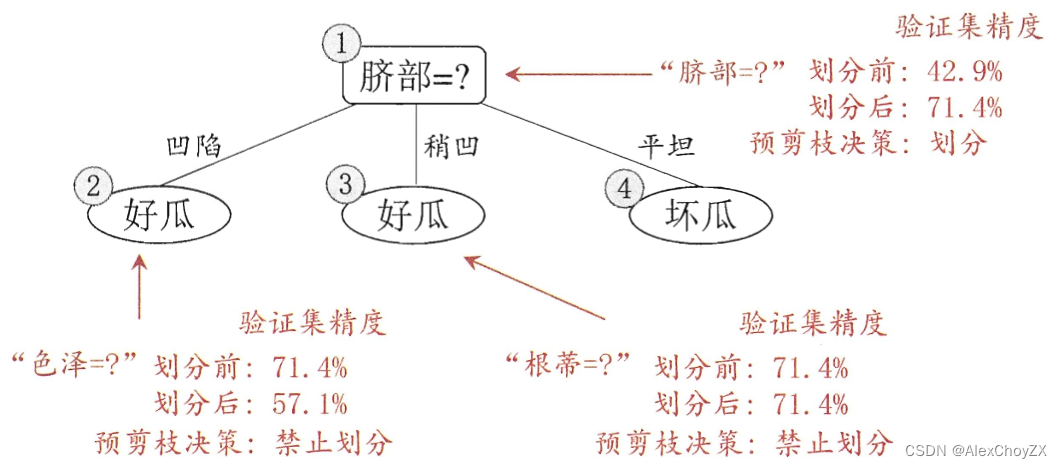
• 对比可看出，预剪枝使得决策树的很多分支都没有展开，这不仅降低了过拟合的风险，还显著减少了决策树的训练时间开销和测试时间开销。但另一方面，有些分支的当前划分虽不能提升泛化性能、甚至可能导致泛化性能暂时下降，但在其基础上进行的后续划分却有可能导致性能显著提高；预剪枝基于“贪心” 本质禁止这些分支展开，给预剪枝决策树带来了欠拟合的风险

2. 后剪枝

• 后剪枝是先从训练集生成一棵完整的决策树， 然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点
• 后剪枝决策树：
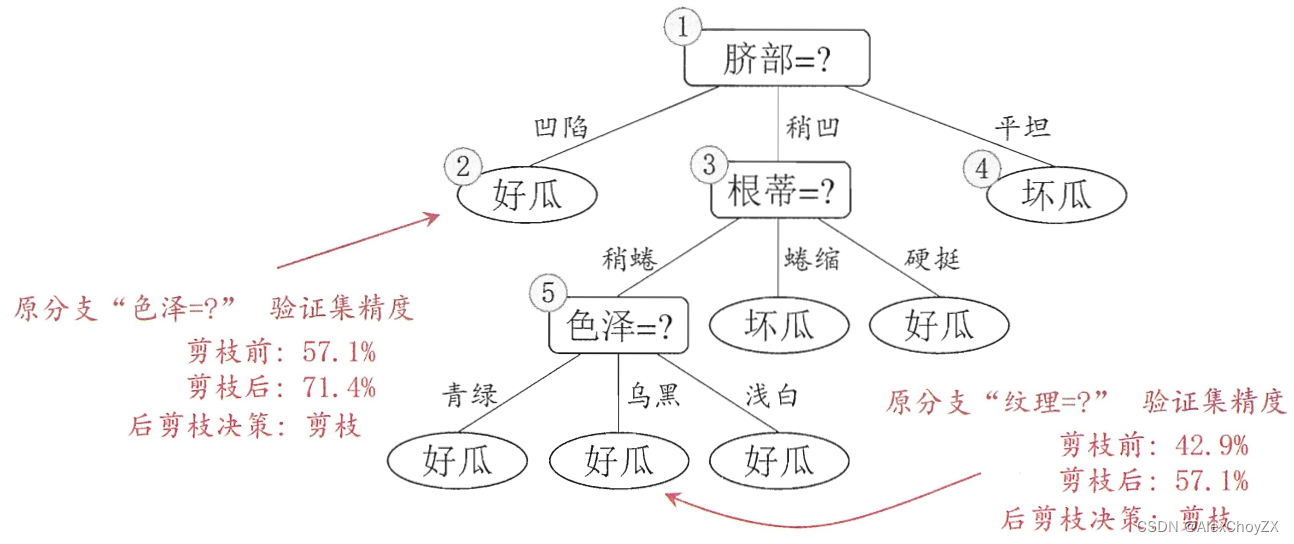
• 对比可看出，后剪枝决策树通常比预剪枝决策树保留了更多的分支。一般情形下，后剪枝决策树的欠拟合风险很小，泛化性能往往优于预 剪枝决策树，但后剪枝过程是在生成完全决策树之后进行的，并且要自底向上 地对树中的所有非叶结点进行逐一考察，因此其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多。

4. 连续与缺失值

连续值处理

• 使用连续属性离散化技术，最简单的策略是采用二分法
  • 给定样本集 $D$ 和连续属性 $a$ ，假定 $a$ 在 $D$ 上出现了 $n$ 个不同的取值，将这些值从小到大进行排序，记为 { a 1 , a 2 , . . . , a n } \{a^1,a^2,...,a^n\} {a1,a2,...,an} 。
  • 基于划分点 $t$ 可将 $D$ 分为子集 $D_t^{-}$ 和 $D_t^{+}$ ，其中 $D_t^{-}$ 包含那些在属性 $a$ 上取值不大于 $t$ 的样本。显然，对相邻的属性取值 $a^i$ 与 $a^{i+1}$ 来说， $t$ 在区间 $[a^i,a^{i+1})$ 中取任意值所产生的划分结果相同。因此，对连续属性 $a$ ，我们可考察包含 $n-1$ 个元素的候选划分点集合 T a = { a i + a i + 1 2 ∣ 1 ≤ i ≤ n − 1 } T_a=\{\frac{a^i+a^{i+1}}{2}|1\leq i\leq n-1 \} Ta​={2ai+ai+1​∣1≤i≤n−1} ，即把区间 $[a^i,a^{i+1})$ 的中位点作为候选划分点。
  • 选取最优的划分点进行样本集合的划分： G a i n ( D , a ) = max ⁡ t ∈ T a G a i n ( D , a , t ) = max ⁡ t ∈ T a E n t ( D ) − ∑ λ ∈ { − , + } ∣ D t λ ∣ ∣ D ∣ E n t ( D t λ ) Gain(D,a)=\max\limits_{t\in T_a}Gain(D,a,t)=\max\limits_{t\in T_a}Ent(D)-\sum\limits_{\lambda\in\{-,+\}}\frac{|D_t^{\lambda}|}{|D|}Ent(D_t^\lambda) Gain(D,a)=t∈Ta​max​Gain(D,a,t)=t∈Ta​max​Ent(D)−λ∈{−,+}∑​∣D∣∣Dtλ​∣​Ent(Dtλ​)，其中 $Gain(D,a,t)$ 是样本集 $D$ 基于划分点 $t$ 二分后的信息增益

缺失值处理

• 常用的缺失值填充方法是:对于连续属性，采用该属性的均值进行填充;对于离散属性，采用属性值个数最多的样本进行填充。这实际上 假设了数据集中的样本是基于独立同分布采样得到的。
• 给定训练集 $D$ 和属性 $a$，$a$ 有 $V$ 个可取值 { a 1 , a 2 , . . . , a V } \{a^1,a^2,...,a^V\} {a1,a2,...,aV}
  • $\tilde{D}$： $D$ 中在属性 $a$ 上没有缺失值的样本子集
  • ${\tilde{D}}^v$：$\tilde{D}$ 中在属性 $a$ 上取值为 $a^v$ 的样本子集
  • ${\tilde{D}}_k$：$\tilde{D}$ 中属于第 $k(k=1,2,...,|\mathcal{Y}|)$ 类的样本子集
  • $w_x$：样本 $x$ 的权重
  • 无缺失值样本所占比例：$\rho =\frac{{\sum }_{x\in \tilde{D}}{w}_x}{{\sum }_{x\in D}{w}_x}$
  • 无缺失值样本中第 $k$ 类所占的比例：${\tilde{p}}_k=\frac{{\sum }_{x\in {\tilde{D}}_k}{w}_x}{{\sum }_{x\in \tilde{D}}{w}_x}$
  • 无缺失值样本中在属性 $a$ 上取值 $a^v$ 的样本所占比例：${\tilde{r}}_v=\frac{{\sum }_{x\in {\tilde{D}}^v}{w}_x}{{\sum }_{x\in \tilde{D}}{w}_x}$
• $Gain(D,a)=\rho \times Gain(\tilde{D},a)=\rho \times [Ent(\tilde{D})-\sum _{v=1}^V{\tilde{r}}_{v}Ent({\tilde{D}}^v)]$
  • 其中：$Ent(\tilde{D})=-\sum _{k=1}^{|\mathcal{Y}|}{\tilde{p}}_k{\log }_2{\tilde{p}}_k$

1. 如何在属性值缺失的情况下进行划分属性选择： 仅可根据 $\tilde{D}$ 来判断属性 $a$ 的优劣
2. 给定划分属性，若样本在该属性上的值缺失，如何对样本进行划分?
   • 若样本 $x$ 在划分属性 $a$ 上的取值已知，则将 $x$ 划入与其取值对应的子结点，且样本权值在子结点中保持为 $w_x$
   • 若样本 $x$ 在划分属性 $a$ 上的取值未知，则将 $x$ 同时划入所有子结点，且样本权值在与属性值 $a^v$ 对应的子结点中调整为 ${\tilde{r}}_v\cdot w_x$
   • 直观地看，这就是让同一个样本以不同的概率划入到不同的子结点中去

5. 多变量决策树

习题