西瓜书 3. 线性模型

数学理论

线性回归

• 线性回归：$y=w^{T}x+b$
• 对数线性回归：$\ln y=w^{T}x+b$
• 广义线性模型：$y=g^{-1}(w^{T}x+b)$
  • $g(\cdot )$ ：联系函数，必须单调可微

对数几率回归

• 线性回归模型产生的预测值：$z=w^{T}x+b$
• 对数几率函数：$y=\frac{1}{1+e^{-z}}$
• 将对数几率函数作为$g^{-1}(\cdot )$代入广义线性模型：$y=\frac{1}{1+e^{-(w^{T}x+b)}}$
• 等价变换：$\ln \frac{y}{1-y}=w^{T}x+b$
  • 将 $y$ 视为样本 $x$ 作为正例的可能性，则 $1-y$ 是其反例可能性
  • 两者的比例 $\frac{y}{1-y}$ 即为几率
  • $\ln \frac{y}{1-y}$ 即为对数几率
• 等价变换：$\ln \frac{p(y=1|x)}{p(y=0|x)}=w^{T}x+b$
  • $p(y=1|x)=\frac{e^{w^{T}x+b}}{1+e^{w^{T}x+b}}$
  • $p(y=0|x)=\frac{1}{1+e^{w^{T}x+b}}$
• 最大似然估计
  • 最大化对数似然函数：$l(w,b)=\sum _{i=1}^m\ln p(y_i|x_i;w,b)$
    • $令\beta =(w;b),\hat{x}=(x;1),则w^{T}x+b={\beta }^T\hat{x}$
    • $令p_1(\hat{x};\beta )=p(y=1|\hat{x};\beta )$
    • $令p_0(\hat{x};\beta )=p(y=0|\hat{x};\beta )=1-p_1(\hat{x};\beta )$
  • 等价变换：$p(y_i|x_i;w,b)=y_i{p}_1({\hat{x}}_i;\beta )+(1-y_i)p_0({\hat{x}}_i;\beta )$
  • 等价于最小化凸函数：$l(\beta )=\sum _{i=1}^m[-y_i{\beta }^T{\hat{x}}_i+\ln (1+e^{{\beta }^T{\hat{x}}_i})]$
  • 用梯度下降法或牛顿法可求出：${\beta }^{\ast }=\underset{\beta }{\mathrm{argmin}}l(\beta )$

线性判别分析LDA（二分类）

• 给定训练样例集，设法将样例投影到一条直线上， 使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;在对新样 本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别
  
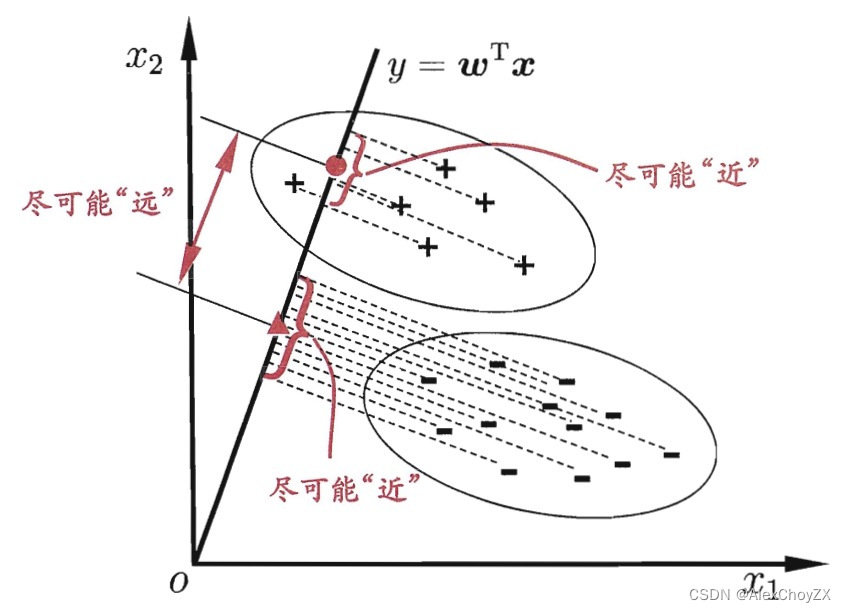
• 符号设定
  • 数据集： D = { ( x i , y i ) } i = 1 m , y i ∈ { 0 , 1 } D=\{(x_i,y_i)\}_{i=1}^m,y_i\in\{0,1\} D={(xi​,yi​)}i=1m​,yi​∈{0,1}
  • 第 i ∈ { 0 , 1 } i\in\{0,1\} i∈{0,1}类示例的集合：$X_i$
  • 第 i ∈ { 0 , 1 } i\in\{0,1\} i∈{0,1}类示例的均值向量：${\mu }_i$
  • 第 i ∈ { 0 , 1 } i\in\{0,1\} i∈{0,1}类示例的协方差矩阵：${\Sigma }_i$
• 投影到直线 $w$ 上
  • 两类样本中心的投影：$w^T{\mu }_0,w^T{\mu }_1$
  • 两类样本所有投影的协方差：$w^T{\Sigma }_{0}w,w^T{\Sigma }_{1}w$
  • 类内散度矩阵：$S_w={\Sigma }_0+{\Sigma }_1=\sum _{x\in X_0}(x-{\mu }_0)(x-{\mu }_0{)}^T+\sum _{x\in X_1}(x-{\mu }_1)(x-{\mu }_1{)}^T$
  • 类间散度矩阵：$S_b=({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T$
• 目标函数
  • 同类样例的投影点尽可能接近：$w^T{\Sigma }_{0}w+w^T{\Sigma }_{1}w$尽可能小
  • 异类样例的投影点尽可能远离：$\Vert w^T{\mu }_0-w^T{\mu }_1{\Vert }_2^2$尽可能大
  • 同时考虑两者：最大化广义瑞利商
    • $\underset{w}{\max }J=\underset{w}{\max }\frac{\Vert w^T{\mu }_0-w^T{\mu }_1{\Vert }_2^2}{w^T{\Sigma }_{0}w+w^T{\Sigma }_{1}w}=\underset{w}{\max }\frac{w^T({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^{T}w}{w^T({\Sigma }_0+{\Sigma }_1)w}=\underset{w}{\max }\frac{w^T{S}_{b}w}{w^T{S}_{w}w}$
  • 等价于$$\{\begin{array}{r}\underset{w}{\min }-w^T{S}_{b}w\\ s.t.w^T{S}_{w}w=1\end{array}$$
• 拉格朗日乘子法
  • 拉格朗日函数： $L(w,\lambda )=-w^T{S}_{b}w+\lambda (w^T{S}_{w}w-1)$
  • 解得：$S_{b}w=\lambda S_{w}w$
    • $即：({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^{T}w=\lambda S_{w}w$
    • $即：w=\frac{({\mu }_0-{\mu }_1{)}^{T}w}{\lambda }{S}_w^{-1}({\mu }_0-{\mu }_1)$
  • 由于广义瑞利商 $J$ 的分子分母均为关于 $w$ 的二次项，因此不关心 $w$ 的大小，只关心其方向。通过调整 $w$ 的大小使得标量 $({\mu }_0-{\mu }_1{)}^{T}w=\lambda$，得：$w=S_w^{-1}({\mu }_0-{\mu }_1)$
• 奇异值分解
  • $S_w=U\Sigma V^T$
  • $S_w^{-1}=U{\Sigma }^{-1}{V}^T$

多分类学习

将LDA推广到多分类任务

• 符号设定
  • 假设存在 $N$ 个类，其中第 $i$ 类示例数为 $m_i$
  • 所有示例的均值向量：$\mu$
  • 类内散度矩阵：$S_w=\sum _{i=1}^N{S}_{w_i}$
    • $S_{w_i}=\sum _{x\in X_i}(x_i-{\mu }_i)(x_i-{\mu }_i{)}^T$
  • 全局散度矩阵：$S_t=\sum _{i=1}^m(x_i-\mu )(x_i-\mu {)}^T$
  • 类间散度矩阵：$S_b=S_t-S_w=\sum _{i=1}^N{m}_i({\mu }_i-\mu )({\mu }_i-\mu {)}^T$
• 目标函数
  • $$\underset{W}{\max }\frac{\sum _{i=1}^{N-1}{w}_i^T{S}_b{w}_i}{\sum _{i=1}^{N-1}{w}_i^T{S}_w{w}_i}=\underset{W}{\max }\frac{tr(W^T{S}_{b}W)}{tr(W^T{S}_{w}W)}$$
    • 其中$W=(w_1,w_2,...,w_{N-1})\in {\mathbb{R}}^{d\times (N-1)}$
    • 等价于：$$\{\begin{array}{r}\underset{W}{\min }-tr(W^T{S}_{b}W)\\ s.t.tr(W^T{S}_{w}W)=1\end{array}$$
  • 另一种常见的优化目标形式：$$\underset{W}{\max }\frac{\prod _{i=1}^{N-1}{w}_i^T{S}_b{w}_i}{\prod _{i=1}^{N-1}{w}_i^T{S}_w{w}_i}=\underset{W}{\max }\prod _{i=1}^{N-1}\frac{w_i^T{S}_b{w}_i}{w_i^T{S}_w{w}_i}$$
• 拉格朗日乘子法
  • 拉格朗日函数：$L(W,\lambda )=-tr(W^T{S}_{b}W)+\lambda [tr(W^T{S}_{w}W)-1]$
    • 解得：$S_{b}W=\lambda S_{w}W$
    • $W$ 的闭式解是 $S_w^{-1}{S}_b$的 $N-1$ 个最大广义特征值所对应的特征向量组成的矩阵。但此处并不能直观地解释为什么要这么构造，因此改用下面的拉格朗日函数求解。
  • 拉格朗日函数：$L(W,\Lambda )=-tr(W^T{S}_{b}W)+tr[\Lambda (W^T{S}_{w}W-I)]$
    • 其中：$I\in {\mathbb{R}}^{(N-1)\times (N-1)}$ 为单位矩阵；$\Lambda =diag({\lambda }_1,{\lambda }_2,...,{\lambda }_{N-1})\in {\mathbb{R}}^{(N-1)\times (N-1)}$ 是由 $N-1$ 个拉格朗日乘子构成的对角矩阵
    • 解得：$S_{b}W=S_{w}W\Lambda$；
      • 展开得：$S_b{w}_i={\lambda }_i{S}_w{w}_i,i=1,2,...,N-1$
      • ${\lambda }_i$对应的是广义特征值，$w_i$ 是 ${\lambda }_i$ 所对应的特征向量
    • 代回目标函数：
      • $\underset{W}{\min }-tr(W^T{S}_{b}W)=\underset{W}{\max }tr(W^T{S}_{b}W)=\underset{W}{\max }\sum _{i=1}^{N-1}{w}_i^T{S}_b{w}_i=\underset{W}{\max }\sum _{i=1}^{N-1}{\lambda }_i{w}_i^T{S}_w{w}_i$
      • 又：$tr(W^T{S}_{w}W)=\sum _{i=1}^{N-1}{w}_i^T{S}_w{w}_i=1$，故在这 $N-1$ 个 ${\lambda }_i$ 都取最大值时上式取最大值
      • 对于 $w_i$ 的实际个数及相关证明，见南瓜书

拆解法

• 将多分类任务拆为若干个二分类任务求解
  • 先对问题进行拆分，然后为拆出的每个二分类任务训练一个分类器
  • 在测试时，对这些分类器的预测结果进行集成以获得最终的多分类结果
  • 考虑 $N$ 个类别 $C_1,C_2,...,C_N$，给定数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } , y i ∈ { C 1 , C 2 , . . . , C N } D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\},y_i\in\{C_1,C_2,...,C_N\} D={(x1​,y1​),(x2​,y2​),...,(xm​,ym​)},yi​∈{C1​,C2​,...,CN​}
• 一对一：One vs One，简称 OvO
  • 将这 $N$ 个类别两两配对，从而产生 $N(N-1)/2$ 个二分类任务
  • OvO 将为区分类别 $C_i$和 $C_j$，训练一个分类器，该分类器把 $D$ 中的 $C_i$ 类样例作为正例，$C_j$ 类样例作为反例
  • 在测试阶段，新样本将同时提交给所有分类器，将得到 $N(N-1)/2$ 个分类结果
  • 最终结果通过投票产生：即把被预测得最多的类别作为最终分类结果
• 一对其余：One vs Rest，简称 OvR
  • OvR每次将一个类的样例作为正例、所有其他类的样例作为反例来训练 $N$ 个分类器
  • 在测试时若仅有一个分类器预测为正类，则对应的类别标记作为最终分类结果
  • 若有多个分类器预测为正类，则通常考虑各分类器的预测置信度，选择置信度最大的类别标记作为分类结果
    
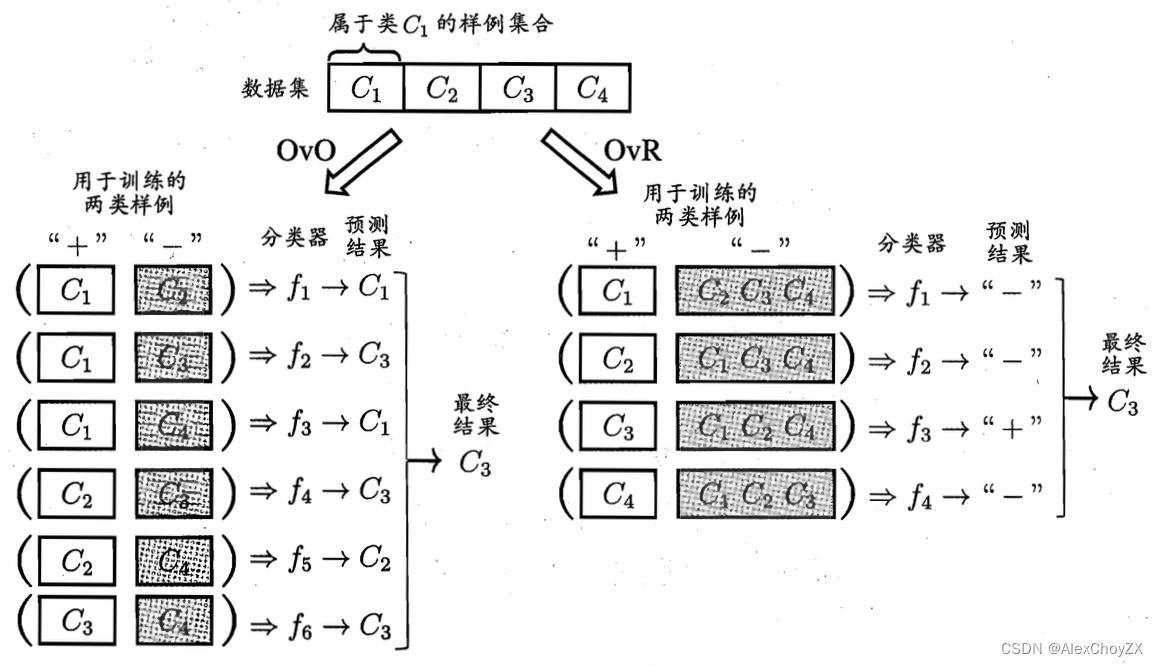
• 多对多：Many vs Many，简称 MvM
  • MvM 是每次将若干个类作为正类，若干个其他类作为反类
  • OvO 和OvR 是 MvM 的特例
  • MvM 的正、反类构造必须有特殊的设计，不能随意选取

类别不平衡问题

• 如果不同类别的训练样例数目稍有差别，通常影响不大，但若差别很大，则会对学习过程造成困扰。类别不平衡(clas s-imbal ance)就是指分类任务中不同类别的训练样例数目差别很大的情况
• 再缩放
  • 几率 $\frac{y}{1-y}$ 反映了正例可能性与反例可能性之比值
  • 阈值设置为 $0.5$ 表明分类器认为真实正、反例可能性相同：分类器决策规则为 $若\frac{y}{1-y}>1则预测为正例$
  • 当训练集中正、反例的数目不同时，令 $m+$ 表示正例数目，$m-$表示反例数目，则观测几率是 $\frac{m^{+}}{m^{-}}$ ，假设训练集是真实样本总体的无偏采样，因此观测几率就代表了真实几率。于是，只要分类器的预测几率高于观测几率就应判定为正例：$若\frac{y}{1-y}>\frac{m^{+}}{m^{-}}，即\frac{y^{\prime }}{1-y^{\prime }}=\frac{y}{1-y}\times \frac{m^{-}}{m^{+}}>1则预测为正例$
• 推断 $\frac{m^{+}}{m^{-}}$ 的方法
  • 欠采样
    • 去除一些反例使得正、反例数目接近，然后再进行学习
  • 过采样
    • 增加一些正例使得正、反例数目接近，然后再进行学习
  • 阈值异动
    • 直接基于原始训练集进行学习，但在用训练好的分类器进行预测时，将 $\frac{y^{\prime }}{1-y^{\prime }}=\frac{y}{1-y}\times \frac{m^{-}}{m^{+}}$ 嵌入到其决策过程中
  • 对比
    • 欠采样法的时间开销通常远小于过采样法，因为前者丢弃了很多反例，使得分类器训练集远小于初始训练集，而过采样法增加了很多正例，其训练集大于初始训练集
    • 过采样法不能简单地对初始正例样本进行重复采样，否则会招致严重的过拟合；过采样法的代表性算法 SMOTE 是通过对训练集里的正例进行插值来产生额外的正例
    • 欠采样法若随机丢弃反例，可能丢失一些重要信息；欠采样法的代表性算法EasyEnsemble 是利用集成学习机制，将反例划分为若干个集合供不同学习器使用，这样对每个学习器来看都进行了欠采样，但在全局来看却不会丢失重要信息

习题

西瓜数据集 3.0α

编号	色泽	根蒂	敲声	纹理	脐部	触感	密度	含糖率	好瓜
1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	0.697	0.46	是
2	乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	0.774	0.376	是
3	乌黑	蜷缩	浊响	清晰	凹陷	硬滑	0.634	0.264	是
4	青绿	蜷缩	沉闷	清晰	凹陷	硬滑	0.608	0.318	是
5	浅白	蜷缩	浊响	清晰	凹陷	硬滑	0.556	0.215	是
6	青绿	稍蜷	浊响	清晰	稍凹	软粘	0.403	0.237	是
7	乌黑	稍蜷	浊响	稍糊	稍凹	软粘	0.481	0.149	是
8	乌黑	稍蜷	浊响	清晰	稍凹	硬滑	0.437	0.211	是
9	乌黑	稍蜷	沉闷	稍糊	稍凹	硬滑	0.666	0.091	否
10	青绿	硬挺	清脆	清晰	平坦	软粘	0.243	0.267	否
11	浅白	硬挺	清脆	模糊	平坦	硬滑	0.245	0.057	否
12	浅白	蜷缩	浊响	模糊	平坦	软粘	0.343	0.099	否
13	青绿	稍蜷	浊响	稍糊	凹陷	硬滑	0.639	0.161	否
14	浅白	稍蜷	沉闷	稍糊	凹陷	硬滑	0.657	0.198	否
15	乌黑	稍蜷	浊响	清晰	稍凹	软粘	0.36	0.37	否
16	浅白	蜷缩	浊响	模糊	平坦	硬滑	0.593	0.042	否
17	青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	0.719	0.103	否

3.2.编程实现对率回归，并给出西瓜数据集 3.0α 上的结果

'''
与原书不同，原书中一个样本xi 为列向量，本代码中一个样本xi为行向量
尝试了两种优化方法，梯度下降和牛顿法。两者结果基本相同，不过有时因初始化的原因，
会导致牛顿法中海森矩阵为奇异矩阵，np.linalg.inv(hess)会报错。以后有机会再写拟牛顿法吧。
'''

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn import linear_model


def sigmoid(x):
    s = 1 / (1 + np.exp(-x))
    return s


def J_cost(X, y, beta):
    '''
    :param X:  sample array, shape(n_samples, n_features)
    :param y: array-like, shape (n_samples,)
    :param beta: the beta in formula 3.27 , shape(n_features + 1, ) or (n_features + 1, 1)
    :return: the result of formula 3.27
    '''
    X_hat = np.c_[X, np.ones((X.shape[0], 1))]
    beta = beta.reshape(-1, 1)
    y = y.reshape(-1, 1)

    Lbeta = -y * np.dot(X_hat, beta) + np.log(1 + np.exp(np.dot(X_hat, beta)))

    return Lbeta.sum()


def gradient(X, y, beta):
    '''
    compute the first derivative of J(i.e. formula 3.27) with respect to beta      i.e. formula 3.30
    ----------------------------------
    :param X: sample array, shape(n_samples, n_features)
    :param y: array-like, shape (n_samples,)
    :param beta: the beta in formula 3.27 , shape(n_features + 1, ) or (n_features + 1, 1)
    :return:
    '''
    X_hat = np.c_[X, np.ones((X.shape[0], 1))]
    beta = beta.reshape(-1, 1)
    y = y.reshape(-1, 1)
    p1 = sigmoid(np.dot(X_hat, beta))

    gra = (-X_hat * (y - p1)).sum(0)

    return gra.reshape(-1, 1)


def hessian(X, y, beta):
    '''
    compute the second derivative of J(i.e. formula 3.27) with respect to beta      i.e. formula 3.31
    ----------------------------------
    :param X: sample array, shape(n_samples, n_features)
    :param y: array-like, shape (n_samples,)
    :param beta: the beta in formula 3.27 , shape(n_features + 1, ) or (n_features + 1, 1)
    :return:
    '''
    X_hat = np.c_[X, np.ones((X.shape[0], 1))]
    beta = beta.reshape(-1, 1)
    y = y.reshape(-1, 1)

    p1 = sigmoid(np.dot(X_hat, beta))

    m, n = X.shape
    P = np.eye(m) * p1 * (1 - p1)

    assert P.shape[0] == P.shape[1]
    return np.dot(np.dot(X_hat.T, P), X_hat)


def update_parameters_gradDesc(X, y, beta, learning_rate, num_iterations, print_cost):
    '''
    update parameters with gradient descent method
    --------------------------------------------
    :param beta:
    :param grad:
    :param learning_rate:
    :return:
    '''
    for i in range(num_iterations):

        grad = gradient(X, y, beta)
        beta = beta - learning_rate * grad

        if (i % 10 == 0) & print_cost:
            print('{}th iteration, cost is {}'.format(i, J_cost(X, y, beta)))

    return beta


def update_parameters_newton(X, y, beta, num_iterations, print_cost):
    '''
    update parameters with Newton method
    :param beta:
    :param grad:
    :param hess:
    :return:
    '''

    for i in range(num_iterations):

        grad = gradient(X, y, beta)
        hess = hessian(X, y, beta)
        beta = beta - np.dot(np.linalg.inv(hess), grad)

        if (i % 10 == 0) & print_cost:
            print('{}th iteration, cost is {}'.format(i, J_cost(X, y, beta)))
    return beta


def initialize_beta(n):
    beta = np.random.randn(n + 1, 1) * 0.5 + 1
    return beta


def logistic_model(X, y, num_iterations=100, learning_rate=1.2, print_cost=False, method='gradDesc'):
    '''
    :param X:
    :param y:~
    :param num_iterations:
    :param learning_rate:
    :param print_cost:
    :param method: str 'gradDesc' or 'Newton'
    :return:
    '''
    m, n = X.shape
    beta = initialize_beta(n)

    if method == 'gradDesc':
        return update_parameters_gradDesc(X, y, beta, learning_rate, num_iterations, print_cost)
    elif method == 'Newton':
        return update_parameters_newton(X, y, beta, num_iterations, print_cost)
    else:
        raise ValueError('Unknown solver %s' % method)


def predict(X, beta):
    X_hat = np.c_[X, np.ones((X.shape[0], 1))]
    p1 = sigmoid(np.dot(X_hat, beta))

    p1[p1 >= 0.5] = 1
    p1[p1 < 0.5] = 0

    return p1


if __name__ == '__main__':
    data_path = r'C:\Users\hanmi\Documents\xiguabook\watermelon3_0_Ch.csv'
    #
    data = pd.read_csv(data_path).values

    is_good = data[:, 9] == '是'
    is_bad = data[:, 9] == '否'

    X = data[:, 7:9].astype(float)
    y = data[:, 9]

    y[y == '是'] = 1
    y[y == '否'] = 0
    y = y.astype(int)

    plt.scatter(data[:, 7][is_good], data[:, 8][is_good], c='k', marker='o')
    plt.scatter(data[:, 7][is_bad], data[:, 8][is_bad], c='r', marker='x')

    plt.xlabel('密度')
    plt.ylabel('含糖量')

    # 可视化模型结果
    beta = logistic_model(X, y, print_cost=True, method='gradDesc', learning_rate=0.3, num_iterations=1000)
    w1, w2, intercept = beta
    x1 = np.linspace(0, 1)
    y1 = -(w1 * x1 + intercept) / w2

    ax1, = plt.plot(x1, y1, label=r'my_logistic_gradDesc')

    lr = linear_model.LogisticRegression(solver='lbfgs', C=1000)  # 注意sklearn的逻辑回归中，C越大表示正则化程度越低。
    lr.fit(X, y)

    lr_beta = np.c_[lr.coef_, lr.intercept_]
    print(J_cost(X, y, lr_beta))

    # 可视化sklearn LogisticRegression 模型结果
    w1_sk, w2_sk = lr.coef_[0, :]

    x2 = np.linspace(0, 1)
    y2 = -(w1_sk * x2 + lr.intercept_) / w2

    ax2, = plt.plot(x2, y2, label=r'sklearn_logistic')

    plt.legend(loc='upper right')
    plt.show()

3.3.选择两个 UCI数据集，比较 10 折交叉验证法和留一法所估计出的对率回归的错误率

• 数据地址

import numpy as np
from sklearn import linear_model
from sklearn.model_selection import LeaveOneOut
from sklearn.model_selection import cross_val_score

data_path = r'C:\Users\hanmi\Documents\xiguabook\Transfusion.txt'

data = np.loadtxt(data_path, delimiter=',').astype(int)

X = data[:, :4]
y = data[:, 4]

m, n = X.shape

# normalization
X = (X - X.mean(0)) / X.std(0)

# shuffle
index = np.arange(m)
np.random.shuffle(index)

X = X[index]
y = y[index]

# 使用sklarn 中自带的api先
# k-10 cross validation
lr = linear_model.LogisticRegression(C=2)

score = cross_val_score(lr, X, y, cv=10)

print(score.mean())

# LOO
loo = LeaveOneOut()

accuracy = 0
for train, test in loo.split(X, y):
    lr_ = linear_model.LogisticRegression(C=2)
    X_train = X[train]
    X_test = X[test]
    y_train = y[train]
    y_test = y[test]
    lr_.fit(X_train, y_train)

    accuracy += lr_.score(X_test, y_test)

print(accuracy / m)

# 两者结果几乎一样

# 自己写一个试试
# k-10
# 这里就没考虑最后几个样本了。
num_split = int(m / 10)
score_my = []
for i in range(10):
    lr_ = linear_model.LogisticRegression(C=2)
    test_index = range(i * num_split, (i + 1) * num_split)
    X_test_ = X[test_index]
    y_test_ = y[test_index]

    X_train_ = np.delete(X, test_index, axis=0)
    y_train_ = np.delete(y, test_index, axis=0)

    lr_.fit(X_train_, y_train_)

    score_my.append(lr_.score(X_test_, y_test_))

print(np.mean(score_my))

# LOO
score_my_loo = []
for i in range(m):
    lr_ = linear_model.LogisticRegression(C=2)
    X_test_ = X[i, :]
    y_test_ = y[i]

    X_train_ = np.delete(X, i, axis=0)
    y_train_ = np.delete(y, i, axis=0)

    lr_.fit(X_train_, y_train_)

    score_my_loo.append(int(lr_.predict(X_test_.reshape(1, -1)) == y_test_))

print(np.mean(score_my_loo))

# 结果都是类似

3.4.编程实现线性判别分析，并给出西瓜数据集 3.0a 上的结果

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt


class LDA(object):

    def fit(self, X_, y_, plot_=False):
        pos = y_ == 1
        neg = y_ == 0
        X0 = X_[neg]
        X1 = X_[pos]

        u0 = X0.mean(0, keepdims=True)  # (1, n)
        u1 = X1.mean(0, keepdims=True)

        sw = np.dot((X0 - u0).T, X0 - u0) + np.dot((X1 - u1).T, X1 - u1)
        w = np.dot(np.linalg.inv(sw), (u0 - u1).T).reshape(1, -1)  # (1, n)

        if plot_:
            fig, ax = plt.subplots()
            ax.spines['right'].set_color('none')
            ax.spines['top'].set_color('none')
            ax.spines['left'].set_position(('data', 0))
            ax.spines['bottom'].set_position(('data', 0))

            plt.scatter(X1[:, 0], X1[:, 1], c='k', marker='o', label='good')
            plt.scatter(X0[:, 0], X0[:, 1], c='r', marker='x', label='bad')

            plt.xlabel('密度', labelpad=1)
            plt.ylabel('含糖量')
            plt.legend(loc='upper right')

            x_tmp = np.linspace(-0.05, 0.15)
            y_tmp = x_tmp * w[0, 1] / w[0, 0]
            plt.plot(x_tmp, y_tmp, '#808080', linewidth=1)

            wu = w / np.linalg.norm(w)

            # 正负样板店
            X0_project = np.dot(X0, np.dot(wu.T, wu))
            plt.scatter(X0_project[:, 0], X0_project[:, 1], c='r', s=15)
            for i in range(X0.shape[0]):
                plt.plot([X0[i, 0], X0_project[i, 0]], [X0[i, 1], X0_project[i, 1]], '--r', linewidth=1)

            X1_project = np.dot(X1, np.dot(wu.T, wu))
            plt.scatter(X1_project[:, 0], X1_project[:, 1], c='k', s=15)
            for i in range(X1.shape[0]):
                plt.plot([X1[i, 0], X1_project[i, 0]], [X1[i, 1], X1_project[i, 1]], '--k', linewidth=1)

            # 中心点的投影
            u0_project = np.dot(u0, np.dot(wu.T, wu))
            plt.scatter(u0_project[:, 0], u0_project[:, 1], c='#FF4500', s=60)
            u1_project = np.dot(u1, np.dot(wu.T, wu))
            plt.scatter(u1_project[:, 0], u1_project[:, 1], c='#696969', s=60)

            ax.annotate(r'u0 投影点',
                        xy=(u0_project[:, 0], u0_project[:, 1]),
                        xytext=(u0_project[:, 0] - 0.2, u0_project[:, 1] - 0.1),
                        size=13,
                        va="center", ha="left",
                        arrowprops=dict(arrowstyle="->",
                                        color="k",
                                        )
                        )

            ax.annotate(r'u1 投影点',
                        xy=(u1_project[:, 0], u1_project[:, 1]),
                        xytext=(u1_project[:, 0] - 0.1, u1_project[:, 1] + 0.1),
                        size=13,
                        va="center", ha="left",
                        arrowprops=dict(arrowstyle="->",
                                        color="k",
                                        )
                        )
            plt.axis("equal")  # 两坐标轴的单位刻度长度保存一致
            plt.show()

        self.w = w
        self.u0 = u0
        self.u1 = u1
        return self

    def predict(self, X):
        project = np.dot(X, self.w.T)

        wu0 = np.dot(self.w, self.u0.T)
        wu1 = np.dot(self.w, self.u1.T)

        return (np.abs(project - wu1) < np.abs(project - wu0)).astype(int)


if __name__ == '__main__':
    data_path = r'C:\Users\hanmi\Documents\xiguabook\watermelon3_0_Ch.csv'

    data = pd.read_csv(data_path).values

    X = data[:, 7:9].astype(float)
    y = data[:, 9]

    y[y == '是'] = 1
    y[y == '否'] = 0
    y = y.astype(int)

    lda = LDA()
    lda.fit(X, y, plot_=True)
    print(lda.predict(X))  # 和逻辑回归的结果一致
    print(y)