深度学习(一):走进机器学习与深度学习理论部分

---

前言

从今天开始，本人将会学习台大李宏毅老师的机器学习课程，将会分享自己的学习内容与收获，从而走进机器学习与深度学习的世界

一、深度学习要干什么？

我们知道y=f(x),深度学习就是为了找出这一个函数映射f(),当你给出训练集，它就会映射出相应的结果。

深度学习则是利用神经网络(Neural Networks)作为这一个映射关系，我们的输入可以是向量(vector),矩阵(matrix),还有序列(sequence),输出可以为回归(regression)与分类(classification)

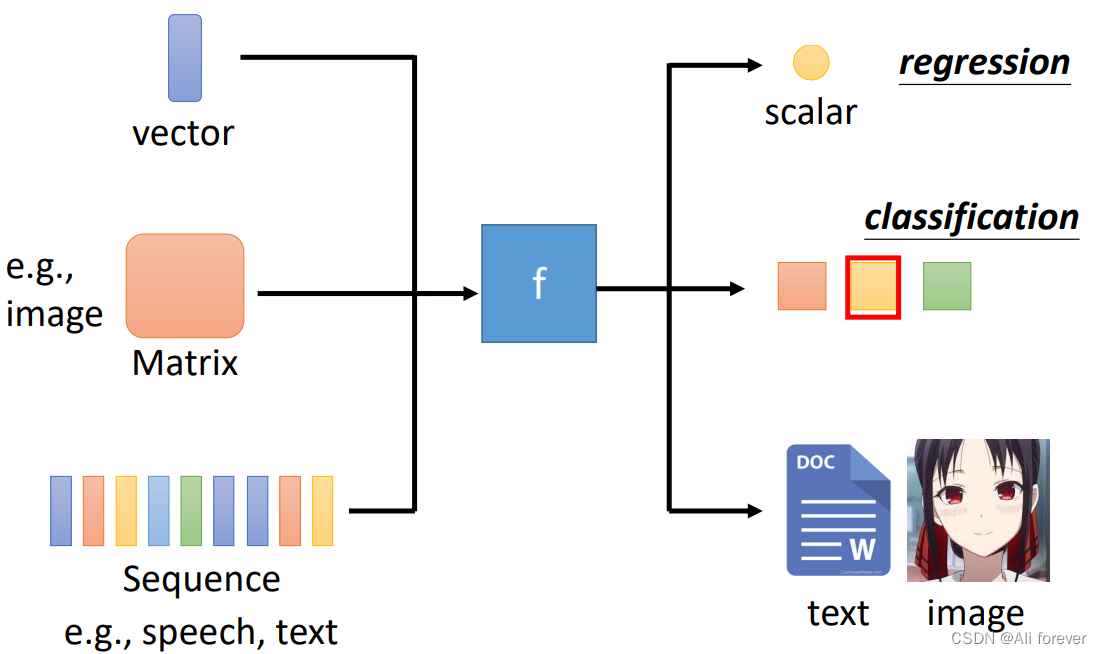
我们来看看神经网络与传统的机器学习有什么不同:

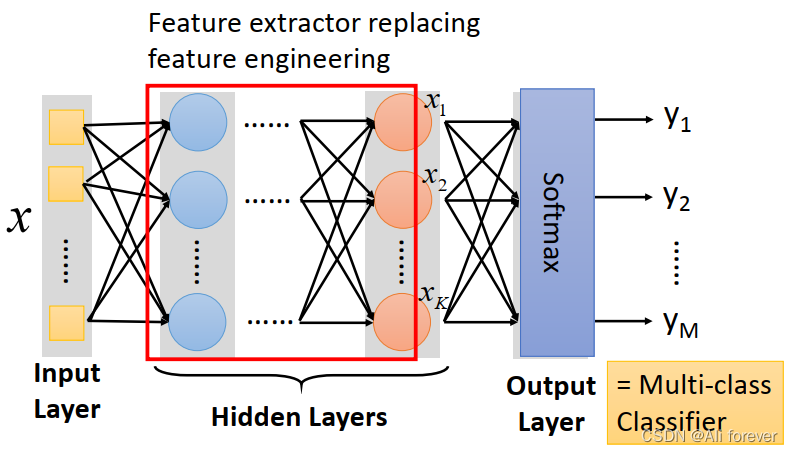
可以看到中间的隐藏层里我们采用了特征提取的方式代替了原本十分复杂的特征工程，特征提取只注重输入的特征数量与输出的特征数量，不需要像特征工程那样创建特征，只需要从原来的特征中提取出特征，降低了维度。
然后我们的输出层经过了一个softmax函数，下面给出softmax函数的定义:
$$\sigma (t)=\frac{e^t}{{\sum }_{i=1}^n{e}^t}$$
值域是(0,1)之间，也就是说输出的结果是一个在零到壹之间的数据，实现了归一化概率

二、初步深度学习过程

1.Function with unknown parameter

$$y=b+w{x}_1$$
其中y是预测值，b是bias(偏差)，w是weight(权重)，x是当前值，也叫特征值(feature),我们的目标是调整b跟w的值使预测值y尽可能准确

2.定义Loss Function

在设定好了我们的模型后，我们就要定义我们的损失函数，以上面的函数举例则为L(b,w),下面举例两种简单的定义方法
绝对误差MAE
$$e=|y-\hat{y}|$$ 均方误差MSE
$$e=|y-\hat{y}{|}^2$$
从而得出Loss function为$$L=\frac{1}{N}\sum _n{e}_n$$
如果y与$\hat{y}$都是概率分布那还可以采用交叉熵(cross-entropy)

3.最佳化Optimization

在定义好Loss Function后我们就要调节参数从而使Loss Function的值最小
$$w^{\ast },b^{\ast }=\arg \underset{w,b}{\min }L$$
我们这时候想到一个方法，梯度下降法(Gradient Descent)

1. 首先随机选取一个点$w^0$。
2. 然后计算$\frac{\partial L}{\partial w}{|}_{w=w^0}$
3. 设定一个超参数学习率(learning rate)$\eta$
4. 利用该公式调整w的值:$w^1=w^0-\eta \frac{\partial L}{\partial w}{|}_{w=w^0}$
5. 如果w的值不再改变了，则代表已经收敛，则可以跳出循环，获得最优化的w，对于b来说也一样。

但是我们发现，这样子优化出来的结果并不能很好的契合我们所预测的结果，所以我们选择更换我们的初始Function，也就是说我们需要更加复杂的模型降低我们的误差

4.优化模型

首先我们可以增加w的数量，利用更加多的特征值x去构造模型，模型就变成
$$y=b+\sum _{j=1}^k{w}_j{x}_j$$
当然这样还不够，这样能够降低一定的误差，但假设我们的图像如红色折线所示,我们还需要把整个模型继续优化

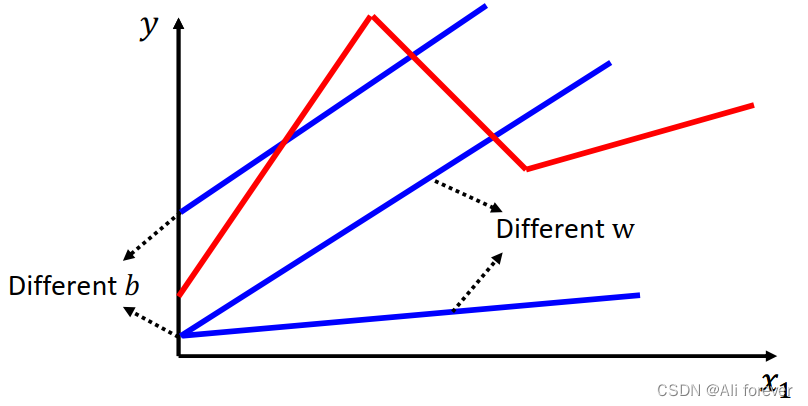
1. Sigmoid Function

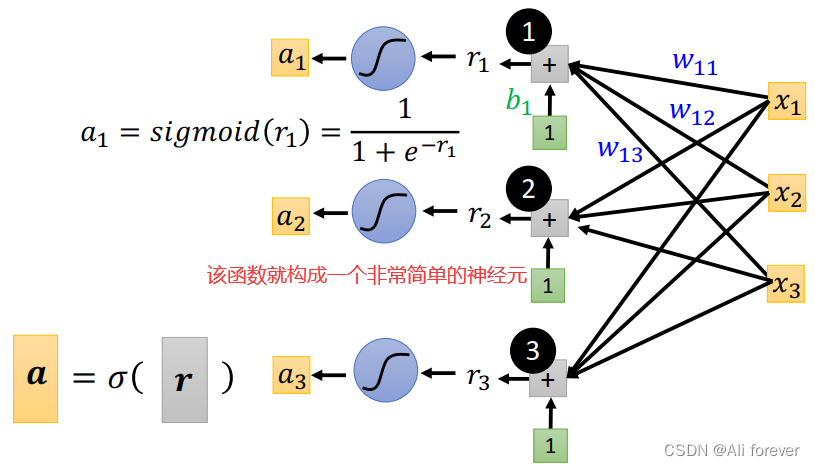
我们可以发现，像这种折线型的数据，我们可以拆分成多个分段函数相加，但是分段函数不好表示，我们需要利用更加生动的函数去迫近该分段函数，我们可以选择Sigmoid Function

我们可以定义新的模型为:
$$y=b+\sum _i{c}_{i}sigmoid(b+\sum _j^k{w}_{ij}{x}_j)$$
其中c是sigmoid函数峰值的大小。

2.矩阵化

当特征值变多时，我们会发现该函数变得十分复杂，这时候我们需要引入矩阵




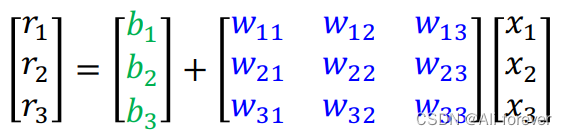
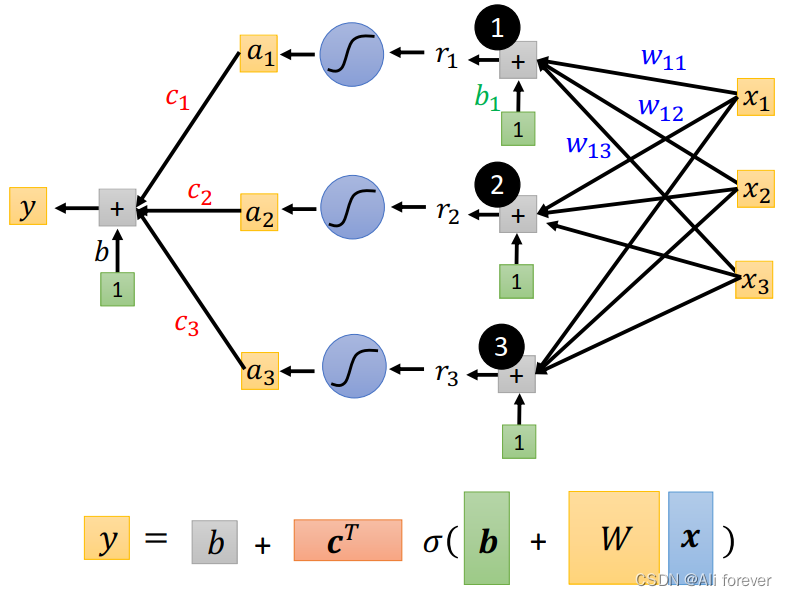
接下来我们需要将所有需要调整的参数展平，这个过程可以称为降维，可以大大降低计算量。

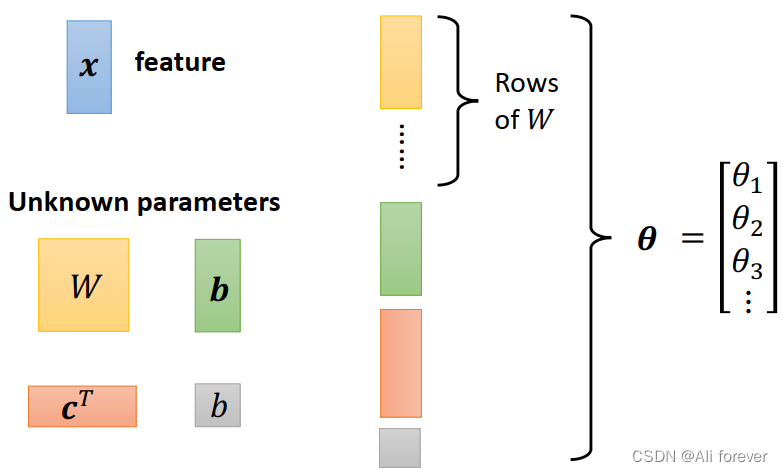
构造完后我们就可以仿照先前的方法，对Loss Function进行最优化处理。但是由于变量过于多，如果还像刚刚那样进行全局的梯度下降速度较慢，这边又采用了一种新的梯度下降方法，小批量梯度下降

每一次小批量梯度下降我们叫做一次train，当所有训练集都训练完之后我们叫做一次epoch，一次epoch包含多次train。

3.ReLU

除了Sigmoid函数我们还有另外一种神经元的激活函数
$$y=b+\sum _{2i}{c}_i\max (0,b+\sum _j^k{w}_{ij}{x}_j)$$
ReLU与Sigmoid函数两者有什么区别呢
效果上：
1.sigmoid函数反向传播时，很容易就会出现梯度消失的情况（在sigmoid接近饱和区时，变换太缓慢，导数趋于0，这种情况会造成信息丢失，从而无法完成深层网络的训练；而ReLU就不会
2.Relu会使一部分神经元的输出为0，这样就造成了网络的稀疏性(对于特征选取更好)，并且减少了参数的相互依存关系，缓解了过拟合问题的发生
性能上：
采用sigmoid等函数，算激活函数时（指数运算），计算量大，反向传播求误差梯度时，求导涉及除法，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多

总结

本文是台大李宏毅机器学习的引言理论部分，希望能帮助到大家进入深度学习的环境中，下面附一张思维导图以加深记忆，下一篇文章将会从代码方面去展示如何用代码实现上述过程。