LeetCode - 买卖股票题目汇总题解（主要采用贪心与动态规划）

---

我的LeetCode主页，一题一题解

---

121. 买卖股票的最佳时机 I（简单）

买卖股票的最佳时机 I:
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock

题目

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票一次），设计一个算法来计算你所能获取的最大利润。

注意：你不能在买入股票前卖出股票。

示例 1:

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

---

解题思路

首先是对题目意思的理解

买卖股票这种事情大家都多少都有耳闻甚至实际操作过，而题目的要求就是简化版

• 题目将给出一个数组，里面将存储全部的股票的价格信息
• 但是在整个遍历的过程中你都只能交易一次

---

题目分析

按时由于在整个过程中都只能交易一次
那么就意味着你只能找一个低点买入一个高点卖出，然后使得中间的差值最大
而且只能买入再卖出，那么低点必然在高点之前
所以就只要遍历一遍就能获得出最终的答案

• 首先将第一点设置为最低点，然后从左到右遍历，寻找最低点
• 如果遇到的价格比最低点高，则尝试买入

---

代码

class Solution {
   
    public int maxProfit(int[] prices) {
   
        //特殊情况
        if(prices.length <= 1) return 0;
        //min记录最小的价格，最小的价格只能出现在当前这天之前，所以只需要获取到当前这天最小的价格就好了
        //res记录结果，即最大差价，res则为最终结果
        int min = prices[0], res = 0;
        for(int i = 1; i < prices.length; i++) {
   
            if(min > prices[i])
                min = prices[i];	// 更新最低价格
            else if(res < prices[i] - min)	//尝试买入
                res = prices[i] - min;	
        }
        return res;
    }
}

---

---

122. 买卖股票的最佳时机 II（简单）

买卖股票的最佳时机 II:
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii

题目

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:

输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

• 1 <= prices.length <= 3 * 10 ^ 4
• 0 <= prices[i] <= 10 ^ 4

---

解题思路

首先是对题目意思的理解

II就是在I的基础上解除了只能进行一次买入操作的限制，快进到无限购买

---

题目分析

贪心

由于操作没有次数限制而且还不手手续费
那不是只要赚差价就好了
只要前一天价格比后一天低，我就赚了这个中间的差价

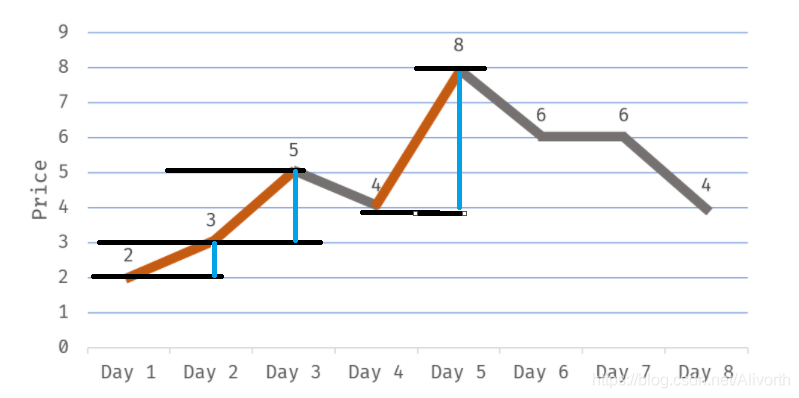
动态规划

同样这个题目也可以用动态规划
首先可以确定每天只有两个状态

1. 空仓

空仓可以由两种状态转换而来

1. 本来就没有，这次继续没有
2. 本来有，但是这次卖了

2. 持仓

持仓可以由两种状态转换而来

1. 本来有，这次继续持有
2. 本来没有，但是这次买入

---

代码

贪心代码

class Solution {
   
    public int maxProfit(int[] prices) {
   
        int res=0;
        for(int i=1; i <= prices.length - 1; i++)
            if(prices[i] > prices[i-1])
                res += prices[i] - prices[i-1];
        return res;
    }
}

动态规划代码

class Solution {
   
    public int maxProfit(int[] prices) {
   
        int n = prices.length;
        int sell = 0, hold = -prices[0];
        for (int i = 1; i < n; ++i) {
   
            sell = Math.max(sell, hold + prices[i]);
            hold = Math.max(hold, sell - prices[i]);
        }
        return sell;
    }
}

---

---

714. 买卖股票的最佳时机含手续费（中等）

买卖股票的最佳时机含手续费：
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/

题目

给定一个整数数组 prices，其中第 i 个元素代表了第 i 天的股票价格 ；非负整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

示例 1:

输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
输出: 8
解释: 能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.

注意:

• 0 < prices.length <= 50000.
• 0 < prices[i] < 50000.
• 0 <= fee < 50000.

---

解题思路

首先是对题目意思的理解

在上一题的基础上加上了手续费，终于不能白嫖了呢

• 无限买卖
• 只能卖空再买
• 每次卖出要收手续费

---

题目分析（简单dp）

因为还是只能卖空再买入，那么简单来说每天最终只会有两个状态：

1. 空仓

空仓可以由两种状态转换而来

1. 本来就没有，这次继续没有
2. 本来有，但是这次卖了

即 dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);

2. 持仓

持仓可以由两种状态转换而来

1. 本来有，这次继续持有
2. 本来没有，但是这次买入

即 dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);

• 其中的卖出是要收手续费的，所以在状态方程中要计入手续费

对于初始状态：
空仓的时候没有就是没有
持仓的时候就说明第一天就买了