实现 8 个概率分布公式及可视化

这篇文章讲介绍几个常见的概率分布公式，以及将他们使用 G2 5.0 可视化出来。

概率和统计知识是数据科学和机器学习的核心，通过数据的分布，从而获取一些有用的信息，获得洞察和结论。

概率分布是一个数学函数，它给出了实验中不同可能结果的发生概率。

了解数据的分布有助于更好地模拟我们周围的世界。它可以帮助我们确定各种结果的可能性，或估计事件的可变性。所有这些都使得了解不同的概率分布在数据科学和机器学习中非常有价值。

均匀分布

最直接的分布是均匀分布。均匀分布是一种概率分布，其中所有结果的可能性均等。例如，如果我们掷一个公平的骰子，落在任何数字上的概率是 1/6。这是一个离散的均匀分布。

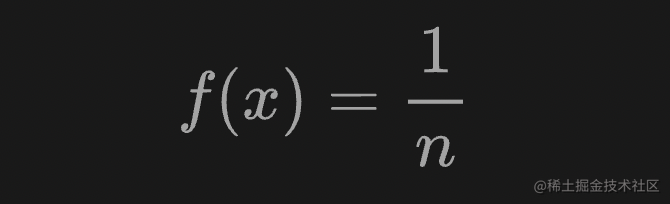
但是并不是所有的均匀分布都是离散的——它们也可以是连续的。它们可以在指定范围内取任何实际值。a 和 b 之间连续均匀分布的概率密度函数 (PDF) 如下：

让我们看看如何在可视化一个骰子的概率分布。

import { Chart } from '@antv/g2';

const chart = new Chart({container: 'container',autoFit: true,
});

const sapme = 10000;
const category = 6;

const data = new Array(sapme).fill(0).map(() => Math.floor(Math.random() * category));

chart.interval().data(data).encode('x', d => d).transform({ type: 'groupX', y: 'count' }).axis('y', { labelFormatter: '~s' });
chart.render(); 

高斯分布

高斯分布可能是最常听到也熟悉的分布。它有几个名字：有人称它为钟形曲线，因为它的概率图看起来像一个钟形，有人称它为高斯分布，因为首先描述它的德国数学家卡尔·高斯命名，还有一些人称它为正态分布，因为早期的统计学家 注意到它一遍又一遍地再次发生。

正态分布的概率密度函数如下：

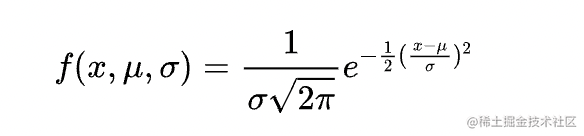
σ 是标准偏差，μ 是分布的平均值。要注意的是，在正态分布中，均值、众数和中位数都是相等的。

当我们绘制正态分布的随机变量时，曲线围绕均值对称——一半的值在中心的左侧，