线性代数常用知识点总结

正交矩阵

实矩阵A满足：
$$AA{}^T=E$$
则A为正交矩阵其中E为单位矩阵。正交矩阵是标准正交基按列排列起来得到的矩阵。

正交矩阵是酉矩阵的在实数域的一种特殊形式。

特征向量&特征值

设A是n阶方阵，如果存在数λ和非零向量ε，使得：
$$A\epsilon =\lambda \epsilon$$
则称λ为方阵A的特征值，ε称为方阵A的特征向量。

相似矩阵

设A，B都是n阶矩阵，如果存在可逆矩阵P，使得：
$$P{}^{-1}AP=B$$
则称A与B相似。

相似矩阵有相同的特征多项式，也就是说A与B有相同的特征值和相同的行列式（det），这是相似矩阵的一个重要性质。下面给出证明：

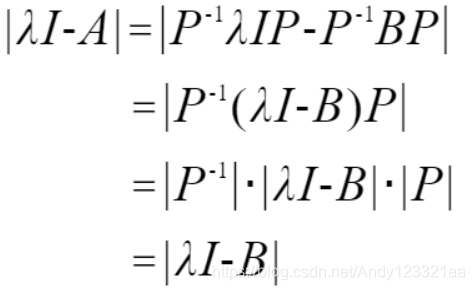
矩阵对角化

对于一个矩阵来讲，对角矩阵在各种计算上比较简单，比如二次型中的标准型就可以用对角矩阵表示。所以如果能将矩阵对角化，就可以方便计算。

n阶方阵A可对角化的充要条件是它有n个线性无关的特征向量。则有：