深度森林原理及实现

Andy_shenzl

已于 2022-12-23 12:37:32 修改

阅读量1.2w

点赞数 11

分类专栏：推荐算法机器学习文章标签：深度学习

于 2020-04-22 16:07:30 首次发布

本文链接：https://blog.csdn.net/Andy_shenzl/article/details/105683388

版权

机器学习同时被 2 个专栏收录

47 篇文章

订阅专栏

推荐算法

14 篇文章

订阅专栏

背景

深度森林(Deep Forest)是周志华教授和冯霁博士在2017年2月28日发表的论文《Deep Forest: Towards An Alternative to Deep Neural Networks》中提出来的一种新的可以与深度神经网络相媲美的基于树的模型，其结构如图所示。

级联森林

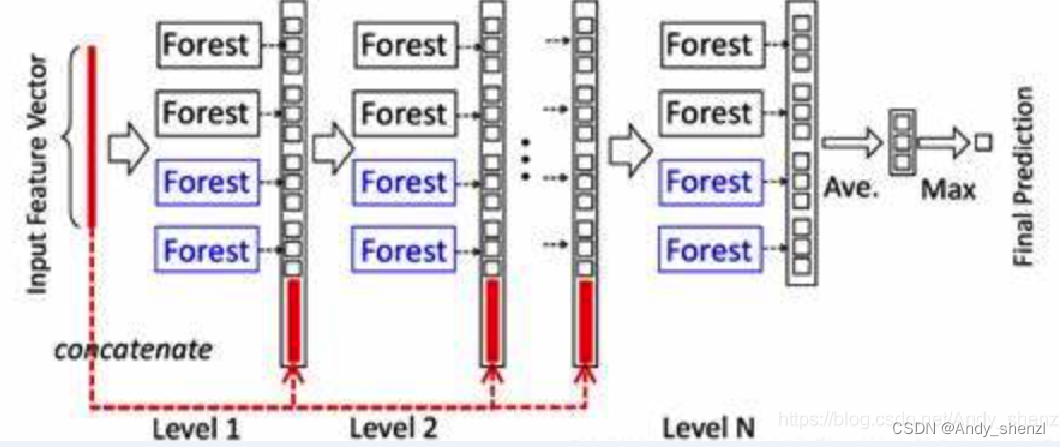
上图表示gcForest的级联结构。

每一层都由多个随机森林组成。通过随机森林学习输入特征向量的特征信息，经过处理后输入到下一层。为了增强模型的泛化能力，每一层选取多种不同类型的随机森林，上图给了两种随机森林结构，分别为completely-random tree forests（蓝色）和random forests（黑色），每种两个。其中，每个completely-random tree forests包含1000棵树，每个节点通过随机选取一个特征作为判别条件，并根据这个判别条件生成子节点，直到每个叶子节点只包含同一类的实例而停止；每个random forests同样包含1000棵树，节点特征的选择通过随机选择√d个特征（d为输入特征的数量），然后选择基尼系数最大特征作为该节点划分的条件。

级联森林的迭代终止条件：迭代到效果不能提升就停止！！！

级联森林中每个森林是如何决策的呢？

每个森林中都包括好多棵决策树，每个决策树都会决策出一个类向量结果（以3类为例，下面也是），然后综合所有的决策树结果，再取均值，生成每个森林的最终决策结果——一个3维类向量！每个森林的决策过程如下图所示。

这样，每个森林都会决策出一个3维类向量，回到图1中，级联森林中的4个森林就都可以决策出一个3维类向量，然后对4个*3维类向量取均值，最后取最大值对应的类别，作为最后的预测结果！

多粒度扫描

多粒度扫描是为了增强级联森林，为了对特征做更多的处理的一种技术手段,具体扫描过程如下图所示。

上图表示对输入特征使用多粒度扫描的方式产生级联森林的输入特征向量。

对于400维的序列数据，采用100维的滑动窗对输入特征进行处理，得到301（400 - 100 + 1）个100维的特征向量。对于20×20的图像数据，采用10×10的滑动窗对输入特征进行处理，得到121（(20-10+1)*(20-10+1)）个10×10的二维特征图。然后将得到的特征向量（或特征图）分别输入到一个completely-random tree forest和一个random forest中（不唯一，也可使用多个森林），以三分类为例，会得到301（或121）个3维类分布向量，将这些向量进行拼接，得到1806（或726）维的特征向量。

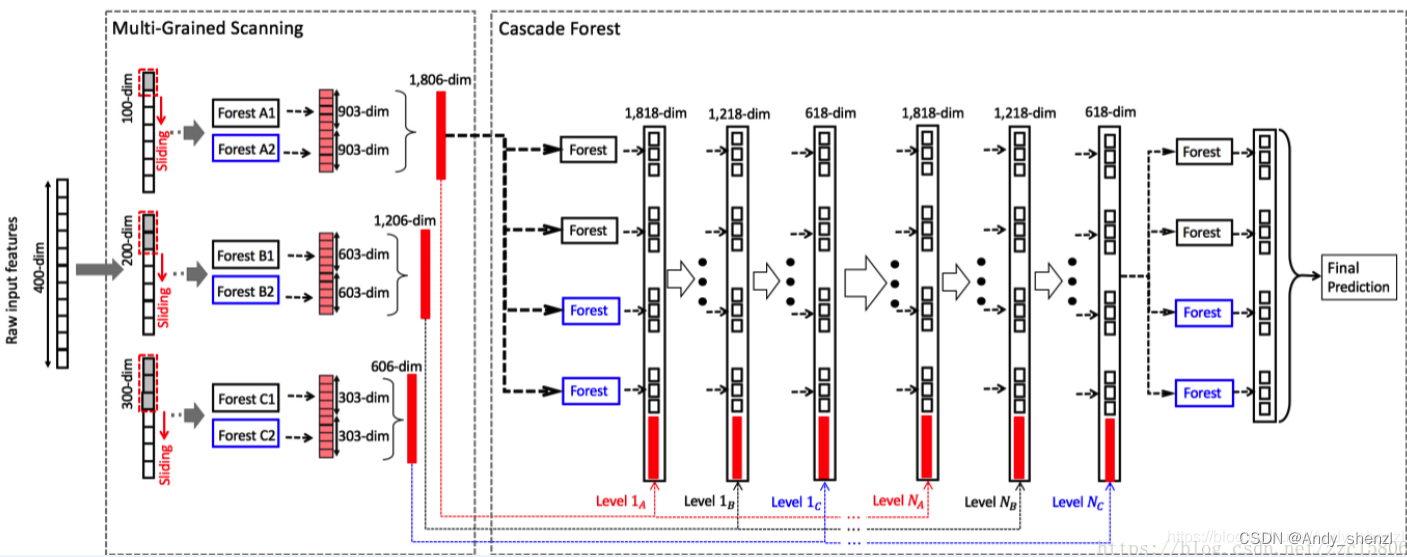
第一步：使用多粒度扫描对输入特征进行预处理。以使用三个尺寸的滑动窗为例，分别为100-dim，200-dim和300-dim。输入数据为400-dim的序列特征，使用100-dim滑动窗会得到301个100-dim向量，然后输入到一个completely-random tree forest和一个random forest中，两个森林会分别得到的301个3-dim向量（3分类），将两个森林得到的特征向量进行拼接，会得到1806-dim的特征向量。同理，使用200-dim和300-dim滑动窗会分别得到1206-dim和606-dim特征向量。

第二步：将得到的特征向量输入到级联森林中进行训练。首先使用100-dim滑动窗得到的1806-dim特征向量输入到第一层级联森林中进行训练，得到12-dim的类分布向量（3分类，4棵树）。然后将得到的类分布向量与100-dim滑动窗得到的特征向量进行拼接，得到1818-dim特征向量，作为第二层的级联森林的输入数据；第二层级联森林训练得到的12-dim类分布向量再与200-dim滑动窗得到的特征向量进行拼接。作为第三层级联森林的输入数据；第三层级联森林训练得到的12-dim类分布向量再与300-dim滑动窗得到的特征向量进行拼接，做为下一层的输入。一直重复上述过程，直到验证收。

代码：

去GitHub上下载源码放在自己python文件夹下的site-packages里面

from gcforest.gcforest import GCForest

运行没有报错，即安装成功

参数配置

#训练的配置，采用默认的模型-即原库代码实现方式
def get_toy_config():
    config = {}
    ca_config = {}
    ca_config["random_state"] = 0  # 0 or 1
    ca_config["max_layers"] = 100 # 最大的层数，layer对应论文中的level
    ca_config["early_stopping_rounds"] = 3 #如果出现某层的三层以内的准确率都没有提升，层中止
    ca_config["n_classes"] = 2 #判别的类别数量
    ca_config["estimators"] = []
    
    ca_config["estimators"].append({"n_folds": 2, "type": "RandomForestClassifier", "n_estimators": 10, "max_depth": None, "n_jobs": -1})
    ca_config["estimators"].append({"n_folds": 2, "type": "ExtraTreesClassifier", "n_estimators": 10, "max_depth": None, "n_jobs": -1})
    ca_config["estimators"].append({"n_folds": 2, "type": "LogisticRegression"})
    config["cascade"] = ca_config #共使用了3个基学习器
    return config

本文只选择了三个模型，没有使用xgboost【xgboost输入格式更加严格，需要调试】

config=get_toy_config()
gc = GCForest(config)
#X_train_enc是每个模型最后一层输出的结果，每一个类别的可能性
X_train_enc = gc.fit_transform(data, label)

y_pred = gc.predict(X_test)
acc = accuracy_score(y_test, y_pred)

Test Accuracy of GcForest = 82.84 %

可以使用gcForest得到的X_enc数据进行其他模型的训练比如xgboost/RF

clf = RandomForestClassifier(n_estimators=1000, max_depth=None, n_jobs=-1)
clf.fit(X_train_enc, label)
y_pred = clf.predict(X_test_enc)
acc1 = accuracy_score(y_test, y_pred)
print("Test Accuracy of Other classifier using gcforest's X_encode = {:.2f} %".format(acc1 * 100))

Test Accuracy of Other classifier using gcforest's X_encode = 79.48 %

完整代码放在GitHub上：Recommendation_algorithm/gcForest.py at master · Andyszl/Recommendation_algorithm · GitHub