数据结构初学过程中对算法效率度量的理解

引例：
对于给定数组a[8]={10,20,30,40,50,60,70,80};
如何将数组前三个元素移到数组后面使得：
a[8]={40,50,60,70,80,10,20,30}?

1、第一种方法（耗费内存）：
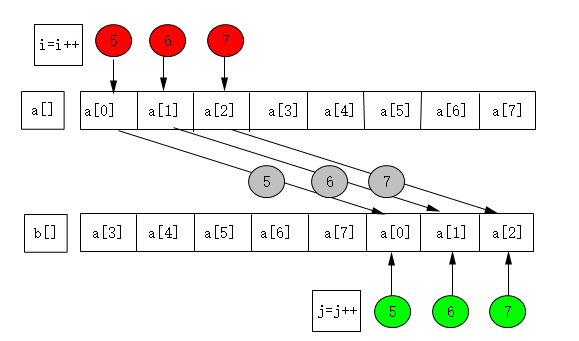
定义一个新的空白数组b[],将a[3]往后的元素依次放入b[0]至b[4],接着将a[0]至a[2]放入b[5]至b[7].最后用代码a[i] = b[i];将元素移入a[]中即可。
（第1步）

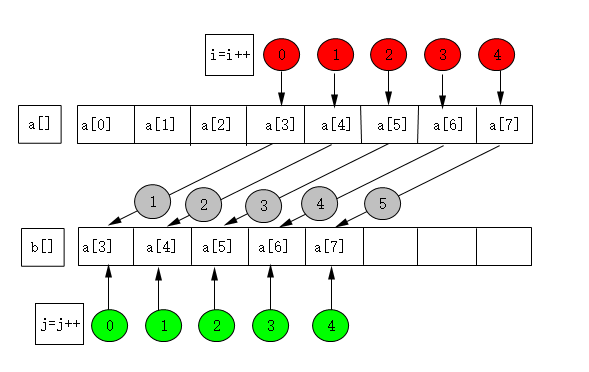
（第2步）

代码如下：

int i,j;
int b[20];

for(i=3,j=0; i<8; i++,j++)
    b[j] = a[i];
for(i=0; j<8; i++,j++)
    b[j] = a[i];
for(i=0; i<8; i++)
    a[i] = b[i];

此种方法，虽然时间复杂度变小了，但是空间复杂度较大。由于分配了一个至少与数组a[]相等的数组b[]的存储空间，在数组a[]长度不是8，而是几千几万时，内存的耗费就显得更为突出。

2、简化思考：
对于a[8]={10,20,30,40,50,60,70,80};如何将10（第一个元素a[0]）移到数组最后(最后一个元素a[7])？
分析：将a[0]内容移到a[7]位置，只需将a[7]内容换成a[0]即可：
即a[7] = a[0];
但是，这样a[7]的原有的数据会丢失，所以应该用以下代码实现：

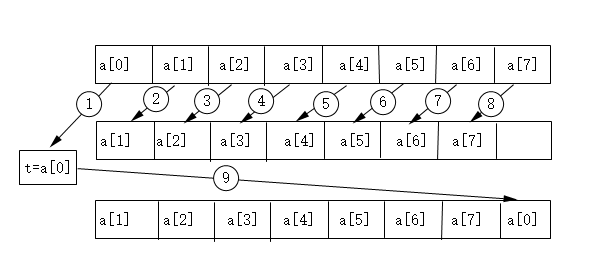
t = a[0];
for(i=0;i<7;i++)
    a[i] = a[i+1];
a[i] = t;

将a[0]的数据先暂时存储在另一变量t所属空间内，然后用for循环将a[i]整体（一个一个按顺序）前移一个位置，最后将a[0]存入a[7]即可。

3、举一反三：
对于要转移的前三个元素，只需要将以上步骤执行三次即可。

for(i=0; i<3; i++)
{
    t = a[0];
    for(j=0; j<7; j++)
        a[j] = a[j+1];
    a[j] = t;
}

此算法，由于旨在数组a[]自身内存及t的内存上做操作，空间复杂度小，但是时间复杂度相对较高，并非最好的算法。

4、如何做到空间复杂度与时间复杂度都比较小：
既要在a[]自身空间内进行操作，又要循环嵌套少一点，函数调用便显得尤为重要：
将a[i]前后调换：

for(i=0,j=0; j>i; i++,j–)
{
    t = a[i];
    a[i] = a[j];
    a[j] = t;
}
for(i=0,j=4; j>i; i++,j–)
{
    t = a[i];
    a[i] = a[j];
    a[j] = t;
}
for(i=5,j=7; j>i; i++,j–)
{
    t = a[i];
    a[i] = a[j];
    a[j] = t;
}

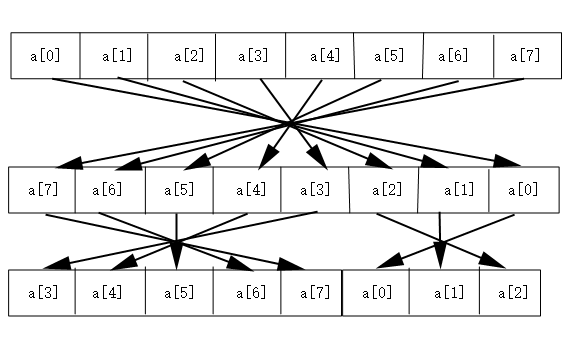
此算法是将置换使用了三次，既没有过分浪费内存，又没有过分浪费时间，时间复杂度和空间复杂度相对来说都较小。但是代码量稍大，可通过函数调用来解决（如下）。

void move_element(int a[],int s,int e)
{
    for(i=5,j=7; j>i; i++,j--)
    {
        t = a[i];
        a[i] = a[j];
        a[j] = t;
    }
}
int main(void)
{
    int i;
    int a[8]={10,20,30,40,50,60,70,80};

    move_element(a,0,7);
    move_element(a,0,4);
    move_element(a,5,7);//函数发送的是数组首元素地址和数组区间（而非长度）

    for(i=0; i<8; i++)
        printf("%-5d",a[i]);
    return 0;
}

到此为止，这个简单的程序算是基本写完了。

5、总结：
（1）所有数据集合的移动算法都可以通过浪费空间来解决，但是都不是理想的算法。
（2）描写算法不可以浪费空间为前提。