最长公共子序列问题(Longest-common-subsequence Problem)简称LCS问题。题目为给定两个序列X、Y求它们的LCS(最长公共子序列),这里的子序列Z的定义为:Z中的元素既在X中也在Y中,并且他们在X、Y中满足严格的下标为一个增序列(假设下标从左到右依次增大)。另外,不要求Z中的元素在X、Y中是连续的,比如当A = {A, B, C, D, B, C, A},B = {B, C, A, D}时,可以有Z = {B, C, D}。现在我们需要求的是LCS,即符合这种条件的最长的一个公共子序列。
而LCS问题是一类动态规划(DP:dynamic programming)问题 。其具有最优子结构性质,定义如下:
设序列 X = {x1,x2,...,xm} 和 Y = {y1,y2,...yn} 的一个最长公共子序列 Z = {z1,z2,...,zk},则:
1> 若 xm=yn,则 zk=xm=yn,且Zk-1是Xm-1和Yn-1的最长公共子序列;
2> 若 xm≠yn且 zk≠xm ,则 Z是 Xm-1和 Y的最长公共子序列;
3> 若 xm≠yn且 zk≠yn ,则 Z是 X和 Yn-1的最长公共子序列;
其中Xm-1={x1,x2,...,xm-1},Yn-1={y1,y2,...yn-1},Zk-1={z1,z2,...,zk-1}。
上面的结论很容易证明。
下面贴上算法导论中的伪代码(其中的数组b可以不用理会,c用于存储Xm和Yn的LCS):
源代码如下(注意:我的源代码中的n是序列X的长度,m是序列Y的长度):
/* 计算LCS,动态规划从前往后推算 */
#include <iostream>
#include <stdio.h>
#include <memory.h>
#define N 1000
char X[N], Y[N]; //序列X、Y
int C[N][N]; //Cij为Xi和Yj的最长公共子序列
int lcs(int n, int m); //计算最长公共子序列
void getAnswer(int n, int m); //构建答案
int main()
{
int m, n;
printf("Enter n and m: ");
while(2 == scanf("%d%d", &n, &m))
{
printf("Enter %d elements for X:", n);
while(getchar() != '\n') continue; //清除回车符等
for(int i = 1; i <= n; ++i)
scanf("%c", &X[i]);
printf("Enter %d elements for Y:", m);
while(getchar() != '\n') continue;
for(int i = 1; i <= m; ++i)
scanf("%c", &Y[i]);
printf("MaxLength: %d\nLCS:", lcs(n, m));
getAnswer(n, m);
printf("\nEnter n and m: ");
}
return 0;
}
int lcs(int n, int m)
{
for(int i = 0; i <= n; ++i)
C[i][0] = 0;
for(int i = 0; i <= m; ++i)
C[0][i] = 0;
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= m; ++j)
{
if(X[i] == Y[j])
C[i][j] = C[i-1][j-1] + 1;
else if(C[i-1][j] >= C[i][j-1])
C[i][j] = C[i-1][j];
else
C[i][j] = C[i][j-1];
}
}
return C[n][m];
}
void getAnswer(int n, int m)
{
if(0 == n || 0 == m)
return;
if((C[n][m] == C[n-1][m-1] + 1) && (X[n] == Y[m])) //一定要判断X[n]和Y[m]是否相等
{
getAnswer(n-1, m-1);
printf("%c", X[n]); //等价于printf("%c", Y[m]);
}
else if(C[n][m] == C[n-1][m])
getAnswer(n-1, m);
else
getAnswer(n, m-1);
}
另一种方法是从后面向前面推算,当然得到的答案也肯能不一样,但一定是最长的:
/* 计算LCS,动态规划从后往前推算 */
#include <iostream>
#include <stdio.h>
#include <memory.h>
#define N 1000
char X[N], Y[N]; //序列X、Y
int C[N][N]; //Cij为Xi和Yj的最长公共子序列
int lcs(int n, int m); //计算最长公共子序列
void getAnswer(int x, int y, int n, int m); //构建答案
int main()
{
int m, n;
printf("Enter n and m: ");
while(2 == scanf("%d%d", &n, &m))
{
printf("Enter %d elements for X:", n);
while(getchar() != '\n') continue; //清除回车符等
for(int i = 1; i <= n; ++i)
scanf("%c", &X[i]);
printf("Enter %d elements for Y:", m);
while(getchar() != '\n') continue;
for(int i = 1; i <= m; ++i)
scanf("%c", &Y[i]);
printf("MaxLength: %d\nLCS:", lcs(n, m));
getAnswer(1, 1, n, m);
printf("\nEnter n and m: ");
}
return 0;
}
int lcs(int n, int m)
{
for(int i = 1; i <= n + 1; ++i)
C[i][0] = 0;
for(int i = 1; i <= m + 1; ++i)
C[0][i] = 0;
for(int i = n; i >= 1; --i)
{
for(int j = m; j >= 1; --j)
{
if(X[i] == Y[j])
C[i][j] = C[i+1][j+1] + 1;
else if(C[i+1][j] >= C[i][j+1])
C[i][j] = C[i+1][j];
else
C[i][j] = C[i][j+1];
}
}
return C[1][1];
}
void getAnswer(int x, int y, int n, int m)
{
if(x == n + 1 || y == m + 1)
return;
if((C[x][y] == C[x+1][y+1] + 1) && (X[x] == Y[y]))
{
printf("%c", X[x]); //等价于printf("%c", Y[y]);
getAnswer(x+1, y+1, n, m);
}
else if(C[x][y] == C[x+1][y])
getAnswer(x+1, y, n, m);
else
getAnswer(x, y+1, n, m);
}
如有疏漏,请批评指正









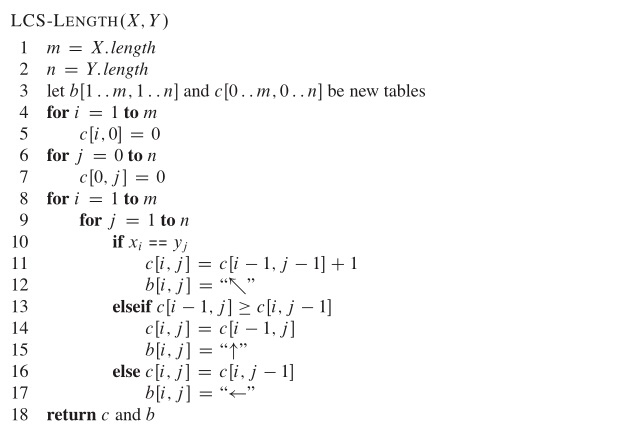














 28万+
28万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








