[算法]PRML学习笔记1.2.5曲线拟合（Curve fitting re-visited）

参考文献：Pattern Recognition and Machine Learning
Published by Springer | January 2006
https://www.microsoft.com/en-us/research/publication/pattern-recognition-machine-learning/

简介

在前面章节的学习中，已经可以看到如何解决多项式曲线拟合（polynomial curve fitting）的问题，可以采用误差最小（error minimization）的方式。现在从概率的角度（probabilistic perspective）回过头来看曲线拟合的问题，从而获得了一些关于误差函数（error functions）和正则化（regularization）的见解，以及走入一个完整的贝叶斯（Bayesian）处理方式。

曲线拟合

曲线拟合问题的目标是由N个输入值$x=(x_1,...,x_N{)}^T$以及$t=(t_1,...,t_N{)}^T$组成的一组训练数据的基础上，给定一组新的输入变量（input variable）$x$，对目标变量（target variable）$t$进行预测。这里可以使用概率分布（probability distribution）来表示目标变量值的不确定性（uncertainty）。为此，这里假设，给定$x$的值，与其相应的$t$值具有高斯分布（Gaussian distribution），其平均值等于（1.1）给出的多项式曲线的值$y(x,w)$。所以, 可以得出公式（1.60）：$$p(t|x,w,\beta )=\mathrm{N}(t|y(w,x),\frac{1}{\beta })$$

在这里，为了与后面的章节中的符号保持一致，定义了一个精度参数（precision parameter ）$\beta$，它对应于分布的反方差（inverse variance ）。图1.16对此进行了示意性说明。

上图为由（1.60）基于给定的$x$给出的$t$的高斯条件分布的示意图，其中平均值由多项式函数$y(x,w)$给出，而精度由参数$\beta$给出，其与方差有关$\beta -1={\sigma }^2$

最大似然（maximum likelihood）

现在使用训练数据$x,t$通过最大似然的方式来确定未知参数$w$和$\beta$的值。如果假设数据是基于（1.60）公式分布中独立（independently）拉取的，则似然函数为如下公式（1.61）：$$p(t|x,w,\beta )=\prod _{n=1}^N\mathrm{N}(t_n|y(x_n,w),\frac{1}{\beta })$$

正如1.2.4中对简单高斯分布所做的那样，将似然函数的对数最大化（maximize the logarithm）是更方便的。替换由（1.46）给出的高斯分布形式，将得到的对数似然函数形式为（1.62）：$$Inp(t|x,w,\beta )=-\frac{\beta }{2}\sum _{n=1}^N(y(x_n,w)-t_n{)}^2)+\frac{N}{2}In\beta -\frac{N}{2}In(2\pi )$$

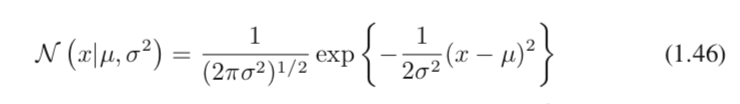
首先考虑确定多项式系数的最大似然解，这将由$wML$表示。 这些是通过相对于$w$最大化（1.62）来确定的。 为此，这里可以省略（1.62）右侧的最后两项，因为它们不依赖于$w$。 另外，这里注意到用正常数系数（positive constant coefficient）对数似然度进行缩放不会改变最大值相对于w的位置，因此可以将系数$\beta$替换为1/2。 最后，代替最大化对数似然（log likelihood,），这里可以等效地使负对数似然最小化（minimize the negative log likelihood）。 因此，可以认为，就确定$w$而言，最大似然等效于最小化由（1.2）定义的平方和误差函数（sum-of-squares error function）。 因此，在高斯噪声分布（Gaussian noise distribution）的假设下，平方和误差函数作为使似然最大化的结果而出现。

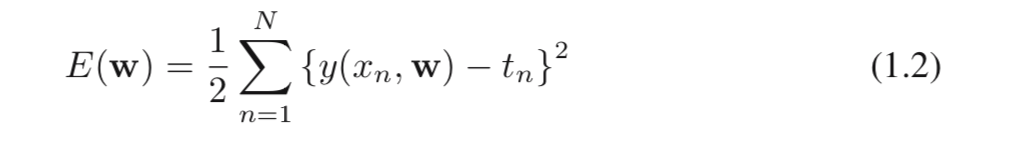
这里还可以使用最大似然来确定高斯条件分布的精度参数β。 相对于$\beta$最大化（1.62）得到如下公式（1.63）：$$\frac{1}{\beta ML}=\frac{1}{N}\sum _{n=1}^N(y(x_n,wML)-t_n{)}^2$$

同样，可以首先确定控制均值的参数向量$wML$，然后像简单的高斯分布一样使用它来找到精度$\beta ML$。

确定参数$w$和$\beta$后，现在可以预测$x$的新值。 因为现在有一个概率模型(probabilistic model)，并且它们用预测分布（predictive distribution）表示，该预测分布给出了$t$上的概率分布(probability distribution)，这不是简单的点估计，而是通过将最大似然参数代入（1.60）得到如下公式（1.64）：$$p(t|x,wML,\beta ML)=\mathrm{N}(t|y(x,wML),\frac{1}{\beta ML})$$

最大后验（maximum posterior）

现在，迈向一种更加贝叶斯的方法，并介绍多项式系数$w$的先验分布（prior distribution）。 为简单起见，这里考虑该形式的高斯分布，如下公式（1.65）：$$p(w|\alpha )=\mathrm{N}(w|0,\frac{I}{\alpha })=(\frac{\alpha }{2\pi }{)}^{(M+1)/2}exp(-\frac{\alpha }{2}{w}^{T}w)$$

其中$\alpha$是分布的精度，M + 1是向量(vector)$w$中第M阶多项式的元素总数。 控制模型参数分布的变量（例如$\alpha$）称为超参数(hyperparameters)。 使用贝叶斯定理，$w$的后验分布（posterior distribution）与先验分布（prior distribution）和似然函数的乘积成比例，如下公式（1.66）展示：$$p(w|x,t,\alpha ,\beta )\alpha p(t|x,w,\beta )p(w|\alpha )$$

现在可以通过在给定数据的情况下找到$w$最可能的值，换句话说，通过最大化后验分布（maximizing the posterior distribution）来确定$w$。 此技术称为最大后验（maximum posterior），或简称为MAP。 取（1.66）的负对数并与（1.62）和（1.65）组合，发现后验的最大值由如下公式（1.67）的最小值给出：$$\frac{\beta }{2}\sum _{n=1}^N(y(x_n,w)-t_n{)}^2+\frac{\alpha }{2}{w}^{T}w$$

因此，看到最大化后验分布等效于最小化前面形式（1.4）中遇到的正则化平方和误差函数(regularized sum-of-squares error function)，且正则化参数由$\lambda =\alpha /\beta$给出。

总结

曲线拟合

1. 目标：给定的输入值$x$以及对应目标变量$t$ - > 建立模型，搭建参数 - > 输入新的输入值$x$ - > 对目标变量$t$进行预测
2. 给定的输入值$x$以及对应目标变量$t$具有高斯分布
3. 精度参数$\beta$与方差有关：$\beta -1={\sigma }^2$

最大似然

1. 数据是独立（independently）拉取的 - > 确定未知参数$w$和$\beta$的值
2. 对数最大化
3. 确定$w$而言，最大似然等效于最小化平方和误差函数
4. 首先确定控制均值的参数向量$wML$，然后像简单的高斯分布一样使用它来找到精度$\beta ML$
5. 确定参数$w$和$\beta$ - > 概率模型 -> 预测$t$上的概率分布
6. 这不是简单的点估计，而是通过将最大似然参数代入

最大后验

1. $w$的先验分布 - > 高斯分布
2. $\alpha$是分布的精度；M + 1是向量(vector)$w$中第M阶多项式的元素总数
3. 超参数(hyperparameters)：控制模型参数分布的变量
4. $w$的后验分布 与 先验分布和似然函数的乘积 成比例
5. 最大化后验分布 (MAP) - > 找到$w$最可能的值
6. 最大化后验分布等效于最小化正则化平方和误差函数；正则化参数$\lambda =\alpha /\beta$