0. 前言
人类很多算法与设计灵感都源于大自然,本文我们要探讨的,就是一种模拟鸟群捕食行为的经典优化算法——粒子群算法 (Particle Swarm Optimization, PSO)。自1995年由Kennedy和Eberhart提出以来,凭借其原理简洁、实现容易、收敛较快等优点,迅速在优化、机器学习、控制工程等多个领域崭露头角。本文将从基本概念出发,剖析其工作原理、算法流程,并通过具体实例帮助读者直观理解PSO的运行机制与应用价值。
1. 什么是粒子群算法?
1.1 基本思想
粒子群算法(Particle Swarm Optimization,PSO),也称粒子群优化算法或鸟群觅食算法,所写为PSO。其属于进化算法的一种,和模拟退火算法相似,它也是从随机解出发,通过迭代寻找最优解,但它没有遗传算法的“交叉”(Crossover) 和“变异”(Mutation) 操作,而是粒子在解空间追随最优的粒子进行搜索。
其灵感来源于对鸟群捕食行为的模拟,在自然界中鸟群觅食一开始是分散的,通过个体间的信息交流和协作,跟踪离食物最近的群体就能够高效地找到食物源,PSO算法正是模拟了这一过程。简单来讲,该算法的思想就是构造一群粒子,粒子群在其周围的空间(也就是问题空间)中移动,不断通过个体信息与群体信息迭代,来寻找它们的最优目标点。
所以PSO算法的核心思想是模拟群体中粒子的行为,每个粒子都有一定的速度和位置,它们根据当前的位置和速度,以及历史最优位置和全局最优位置等信息来调整自己的运动轨迹以寻求最优点。特点是:粒子群算法具有收敛速度快、参数少、算法简单易实现的优点(对高维度优化问题,比遗传算法更快收敛于最优解),同时粒子群算法具有并行性,每个粒子都有记忆,因此对于有些问题可以得到不同的有意义方案。但这种算法也存在陷入局部最优解的问题,因此依赖于良好的初始化。
1.2 通俗理解
我们来具体讲讲鸟群觅食这个例子,以便更好理解粒子群算法。设想这样的场景:有一群鸟(粒子群)在巨大地森林中寻找食物(最优解):
① 首先每只鸟都不知道食物在哪个具体位置;
② 判断位置好坏:但每只鸟都能感受到当前位置离食物大概有多远(适应度值);
③ 记忆并沟通:每只鸟都会记录下自己飞行路线上离食物最近的位置(个体极值);同时每只鸟都有“对讲机”可以互相沟通,所以每只鸟都知道全部鸟中目前找到最近的位置在哪里(全局极值);
④ 移动策略:那么设想这些鸟知道这些信息(个体极值与全局极值)后下一步要怎么走呢?
- 惯性:在飞行方向上有一定惯性,会保持向原来方向一致飞一段;
- 自我认知:会想着往自己最好的位置方向上去飞,飞到自己发现不错的那个位置附近;
- 群体认知:知道群体有更好的位置,也会考虑向那个位置飞。
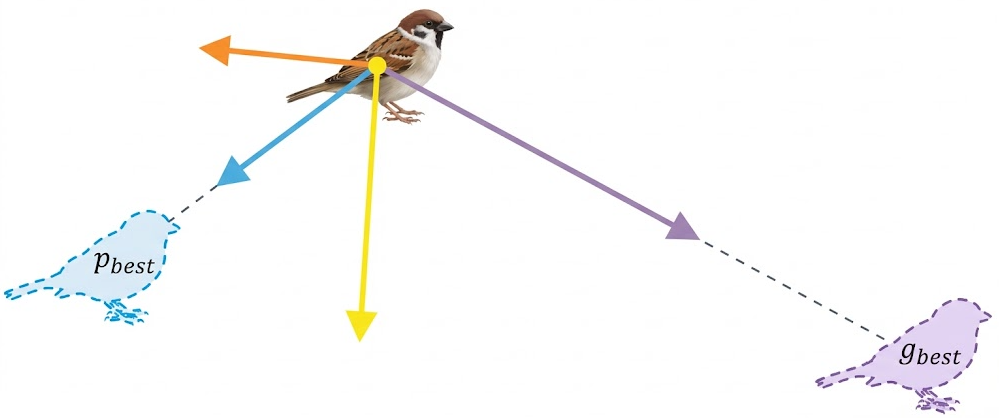
上图是每个鸟下一步飞行方向的策略,与上面讲的移动策略对应,橙色代表惯性方向,蓝色代表自我认知的个体极值(),紫色代表群体极值方位(
),这个黄色就是下一步移动的速度方向。但惯性、个体极值与群体极值一定有比例权重,从而影响下一步的判断,具体我们下面再展开详细说明。
所以可以看出在这个场景下,在“跟随自己最好的经验”和“跟随群体最好的经验”的规则,整个鸟群最终会聚集在食物量最丰富的地方,这就是PSO算法的核心。
2. 算法原理与流程
2.1 基本原理
上面讲到了,粒子群算法从群体活动中获取灵感,每一个个体都会受益于所有成员在这个过程中发现和累积的经验(信息的社会共享)。这个群体中每一个独立的粒子都有自己的速度与位置(两个核心要素)速度表示粒子下一步迭代时移动的方向和距离,位置是所求解问题的一个解。在信息共享的基础上,每个粒子不仅考虑自身的经验(个体最优),还会参考群体的经验(全局最优),这种双重信息利用机制使得算法具有良好的全局搜索能力和收敛性。粒子群优化算法原理简单,在内存需求和计算速度方面的成本较低,是一种能够优化非线性和多维问题的算法。
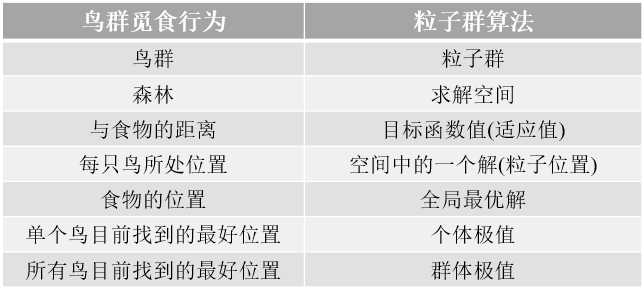
总结以上可以将鸟群觅食行为与粒子群算法的各个部分联系起来,用以下的表格进行一一对应:
2.2 数学模型
我们将这一过程抽象出来,用一些数学表达式来表示。假设在【D维】搜索空间中,有【N个】粒子,每一个粒子就代表了一个解。(注下面讲的是标准PSO算法,有兴趣也可以去了解一下离散型粒子群算法或PSO变体)
粒子维度D:粒子搜索的空间维数即为自变量的个数;
粒子群规模N:为正整数,推荐取值为[20,1000]。简单问题N可以取20~40,难度较大的可以适当提高N。但是较小的粒子群容易陷入局部最优解;较大粒子群可以提高收敛性,能够更快找到全局最优解,但需要的算力也随之提高,而且当粒子群足以解决问题时再继续增大N将不会有太明显的作用。
1. 首先我们先清楚粒子的状态量,如某一时刻粒子的位置、速度、位置好坏、群体粒子最优等如何表示:
① 第 i 个粒子的位置向量为:
② 第 i 个粒子的速度向量(有大小和方向)为:
③ 第 i 个粒子迄今为止搜索到的最优位置(个体极值):
④ 群体搜索到的最优位置:
⑤ 第 i 个粒子搜索到的最优位置的适应值(将位置信息代入目标函数的值)为:
⑥ 群体搜索到的最优位置的适应值为:
2. 下一步粒子该如何迭代更新?
① 速度更新公式(表述上叫速度,实际上就是粒子下一步迭代移动的距离和方向,也就是一个位置向量)


把上面提到的鸟(粒子)移动策略的图拿下来,这样与速度公式对应来看可能更容易理解一些,黄色的向量方向就是迭代向量合后下一步的方向。这里的公式中:
是 t 时刻第 i 个粒子的移动速度(注意实际是移动距离与方向),
是下一时刻 i 粒子的速度;
是 t 时刻第 i 个粒子的位置;
是 t 时刻第 i 个粒子的个体极值;
是 t 时刻的群体极值;
、
分别为个体与群体学习因子,分别调节粒子向“自身经验”和“群体经验”学习的力度;
、
为0~1的随机数,引入随机性以增强算法跳出局部最优的能力;
是惯性权重,代表了粒子对当前自身运动状态的信任程度,粒子依据自身的速度进行惯性运动。当其较大时全局搜索能力较强,当其较小时局部寻优能力较强。通常做法是使算法在前期有较高的全局搜索能力以得到合适的种子,而在后期有较高的局部搜索能力以提高收敛精度,所以这个权重有不同的更新策略以满足更好的寻优。
学习因子
、
的推荐取值范围是[0,4],经典取值为
、
与
等,针对不同的问题有不同的取值,一般通过在一个区间内试凑来调整这两个值。
- 当
,无私型粒子群算法,粒子没有了自我认知能力,变为只有社会认知的模型。粒子有扩展搜索空间的能力,具有较快的收敛速度,但由于缺少局部搜索,对于复杂问题比标准PSO 更易陷入局部最优;
- 当
,自我认知型粒子群算法,完全没有信息的社会共享,整个群体相当于多个粒子进行盲目的随机搜索,导致算法收敛速度缓慢,因而得到最优解的可能性小。
惯性权重更新策略
- 最经典的一种策略为线性递减惯性权重(LDIW):随着迭代次数的增加,惯性权重
不断减小,公式如下:
式中,是初始惯性权重,
是迭代至最大时的惯性权重,t是当前迭代次数,
是最大迭代次数(Tmax一般取[50,70],经典取值60、70、100,需要根据情况调整)。一般惯性权重这里设置为
,
。
当然,也有非线性衰减、随机调整等更复杂的策略,但线性递减因其简单有效,至今仍是工程实践中受欢迎的一种选择。总之的引入使PSO算法性能有了很大的提高,针对不同的搜索问题,可以调整全局和局部搜索能力。
② 位置更新公式
即上一步的位置 + 下一步的速度(向量合),结合上面的速度公式就可以得到迭代的下一步了。
以上式子就是标准粒子群算法的数学模型,还有许多变体,这里不作赘述~
2.3 算法流程
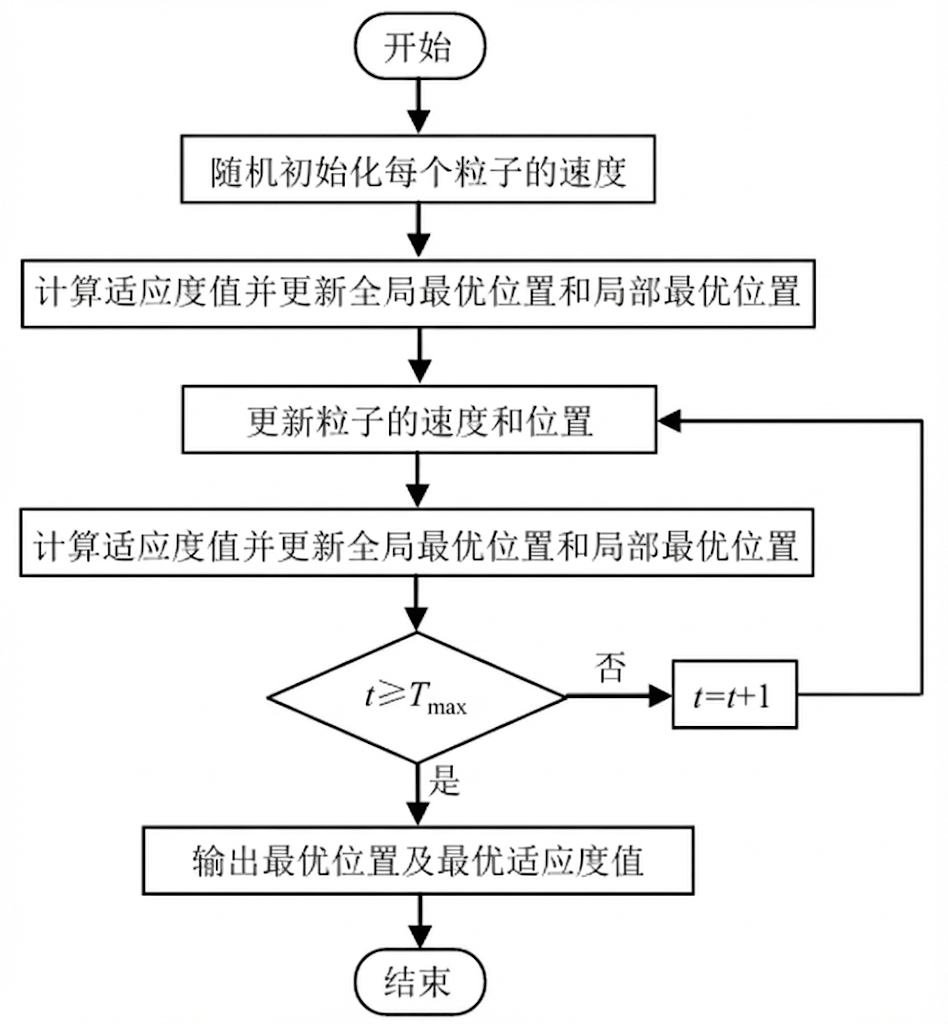
粒子群算法的流程如下:
① 初始化粒子群参数(包括粒子群规模、粒子维度、迭代次数、惯性权重、学习因子等);
② 随机初始化每个粒子的速度与位置;
③ 计算适应度值并更新全局最优位置和局部最优位置;
④代入公式,计算并更新粒子的速度与位置;
⑤再次计算适应度值并更新全局最优位置和局部最优位置;
⑥ 判断是否满足终止条件(达到最大迭代次数或两次迭代之间适应值的最小差值),若满足则跳出循环,否则返回步骤④;
⑦ 输出最优位置及最优适应度值。
3. 算法实战案例
可以利用粒子群算法寻找目标函数的最大值,目标函数为:
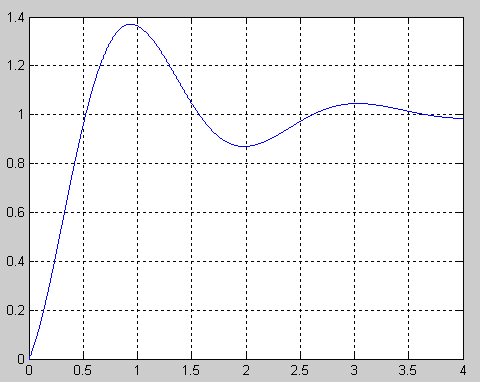
函数曲线图
其中粒子在这个曲线上运动,通过不断改变x的大小来改变粒子在曲线上的位置,因此这个粒子群算法的维度为1,给粒子的搜索范围为[0,4]。所以从粒子群算法的思想来看,我们首先随机选取一些粒子初始位置与速度,调整算法参数等,通过迭代判断最终找到最大值。
以下是完整代码:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# --- 1. 定义目标函数 ---
def target_func(x):
return 1 - np.cos(3 * x) * np.exp(-x)
# --- 2. PSO 算法逻辑 ---
class PSO_1D:
def __init__(self, n_particles=20, max_iter=50):
self.n_particles = n_particles
self.max_iter = max_iter
self.x_min, self.x_max = 0, 4
# 初始化
self.X = np.random.uniform(self.x_min, self.x_max, n_particles)
self.V = np.random.uniform(-0.1, 0.1, n_particles)
self.pbest = self.X.copy()
self.pbest_val = target_func(self.X)
self.gbest = self.X[np.argmax(self.pbest_val)]
self.gbest_val = np.max(self.pbest_val)
# 参数
self.w = 0.7
self.c1 = 1.4
self.c2 = 1.4
def update(self):
r1 = np.random.rand(self.n_particles)
r2 = np.random.rand(self.n_particles)
# 速度更新
self.V = self.w * self.V + \
self.c1 * r1 * (self.pbest - self.X) + \
self.c2 * r2 * (self.gbest - self.X)
self.V = np.clip(self.V, -0.5, 0.5)
# 位置更新
self.X = self.X + self.V
self.X = np.clip(self.X, self.x_min, self.x_max)
# 适应度更新
fitness = target_func(self.X)
improve_mask = fitness > self.pbest_val
self.pbest[improve_mask] = self.X[improve_mask]
self.pbest_val[improve_mask] = fitness[improve_mask]
current_best_val = np.max(fitness)
if current_best_val > self.gbest_val:
self.gbest_val = current_best_val
self.gbest = self.X[np.argmax(fitness)]
return self.X, self.gbest, self.gbest_val
# --- 3. 可视化设置 (优化版) ---
max_frames = 50
pso = PSO_1D(n_particles=15, max_iter=max_frames)
fig, ax = plt.subplots(figsize=(8, 5))
x_line = np.linspace(0, 4, 200)
y_line = target_func(x_line)
# 绘制背景
ax.plot(x_line, y_line, label='Objective Function', color='#1f77b4', alpha=0.8, linewidth=2)
ax.set_xlim(0, 4)
ax.set_ylim(0, 1.8)
ax.set_xlabel('x (Input)')
ax.set_ylabel('y (Fitness)')
ax.set_title('PSO Optimization Process', fontsize=12)
# 绘制动态元素
scat = ax.scatter([], [], c='red', s=50, alpha=0.8, label='Particles', zorder=5)
star, = ax.plot([], [], 'y*', markersize=18, markeredgecolor='black', label='Global Max', zorder=10)
text_info = ax.text(0.02, 0.95, '', transform=ax.transAxes,
fontsize=10, verticalalignment='top',
bbox=dict(boxstyle="round,pad=0.3", fc="white", ec="gray", alpha=0.9))
ax.legend(loc='upper right')
def animate(frame):
X_pos, g_pos, g_val = pso.update()
Y_pos = target_func(X_pos)
scat.set_offsets(np.c_[X_pos, Y_pos])
star.set_data([g_pos], [g_val])
# 动态更新文字
status_text = (
f"Iteration: {frame + 1}/{max_frames}\n"
f"Max Value: {g_val:.5f}\n"
f"Best Pos : {g_pos:.5f}"
)
text_info.set_text(status_text)
if frame == max_frames - 1:
ax.set_title(f'Optimization Completed! Final Result: {g_val:.4f}', color='green', fontweight='bold')
print(f"\n✅ 算法运行结束!")
print(f"最终找到的最大值: {g_val:.6f}")
print(f"对应的坐标 x: {g_pos:.6f}")
return scat, star, text_info,
anim = FuncAnimation(fig, animate, frames=max_frames, interval=100, blit=False, repeat=False)
plt.tight_layout()
plt.show()最终运行效果如下:
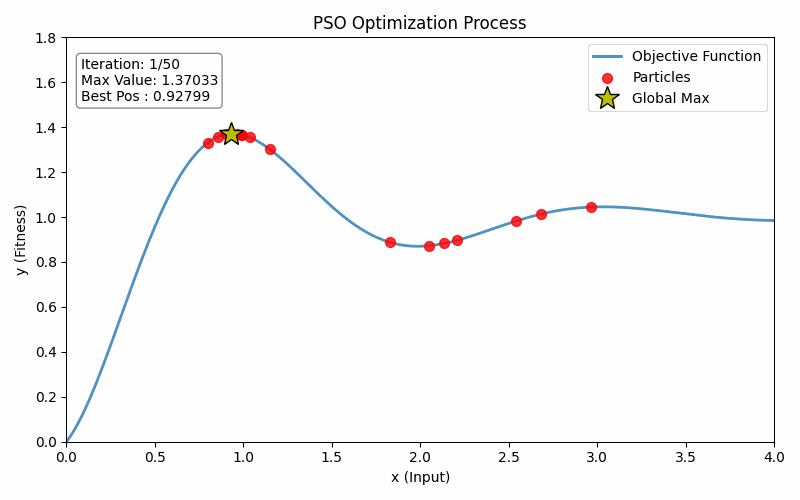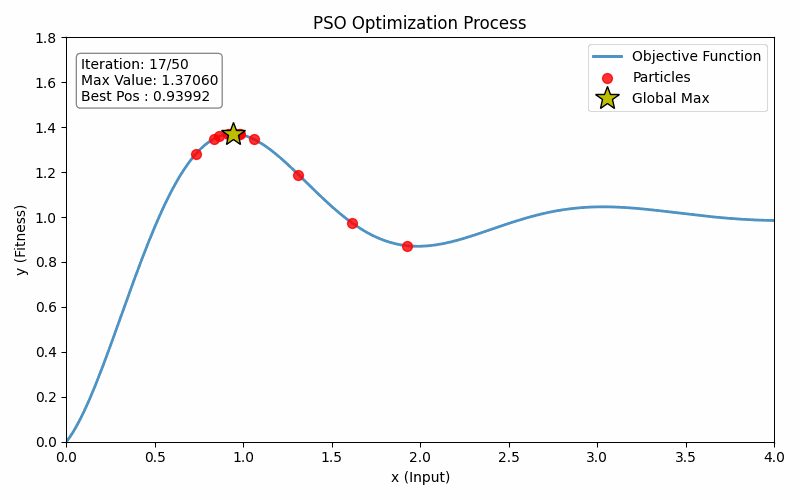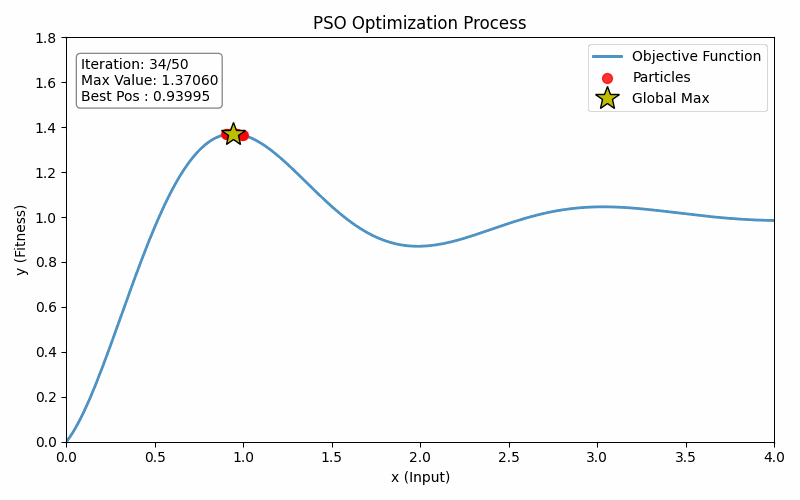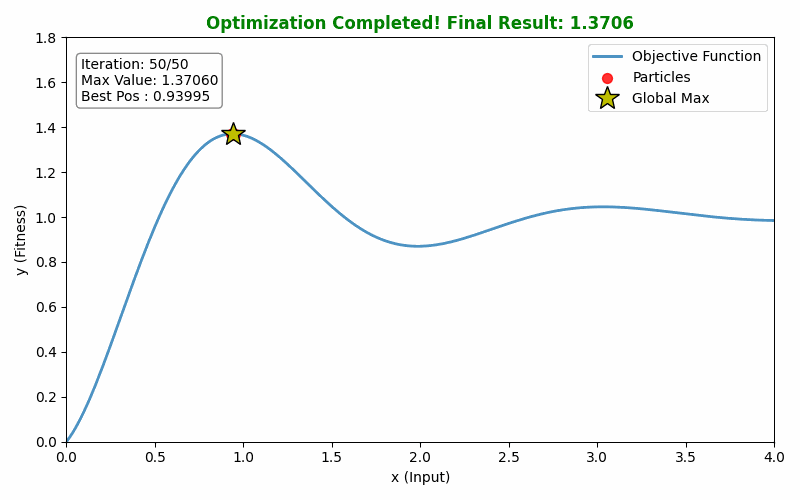
4. 总结
本文从粒子群算法的基本思想出发,介绍了PSO的基本原理、数学模型以及算法的运行流程,最终通过可视化粒子群算法解决函数最值寻优问题。通过模拟鸟群协作觅食的智能行为,PSO以简洁的机制实现了高效的全局搜索能力,不仅易于理解与实现,还在连续优化、工程设计、机器学习等多个领域展现出强大潜力。
声明:本文用于交流学习,如有不足敬请批评指正。
参考来源:知乎_追梦小公子、粒子群算法(2)、CSDN_张博208,若有侵权请联系。





















 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










