算法-二分法和牛顿法求指定精度平方根

一.引言

给定某个整数，给定固定精度，求该整数对应精度的平方根。

假设目标数字为 targrt，则寻找平方根数使得 sqrt(target) = Left = Right = sqrt(Left * Right)

退出条件: Left 与 Right 的整数部分和小数点后N(根据精度要求)位全部相同

二.精度状态检测

实现求平方根方法前首先需要定义一个检查精度的函数，用来检查对应平方根是否是满足精度的平方根。判断方法很简单，根据迭代得到的两个数字 Left 与 Right，去除整数部分，判断小数点后 N 位是否相等，如果满足N满足精度要求且全部相等，则说明满足退出条件。

1.参数说明

Left：平方根1

Right: 平方根2

Target(Int): 目标整数

Precision(Int): 平方根精度要求

2.判断精度

如果精度未达到指定 precision，则直接退出，不判断小数点位数是否相同

3.判断准度

如果精度达到 precision，则判断小数点后 precision 位是否相同，相同则满足退出条件

# 检查结果是否满足精度要求与平方根要求
def check_precision_state(left, right, target, precision):
    # 整数部分长度
    len_num = len(str(target))
    left = str(left)
    right = str(right)
    # 精度未满足要求
    if len(left) <= len_num + precision or len(right) <= len_num + precision:
        return False
    # 精度满足要求，判断小数点后位数是否相等
    for index in range(len_num, len_num + precision):
        if left[index] != right[index]:
            return False
    return True

三.二分法求对应精度平方根

1.思路

(1) 首先猜测一个初始值 init，如果 init * init = target 则直接退出，找到平方根

(2) 如果 init 不满足，则 Left = init ，Right = target / Left 

a.如果 Left < 真实平方根，则 Right > 真实平方根，因为两者乘积固定，所以取 (Left +  Right) / 2 会逼近真实平方根

b.同理，如果 Right < 真实平方根，则 Left > 真实平方根，所以取二者平均会逼近真实平方根

(3) 第二步循环迭代 Left 与 Right，直到二者达到精度检测状态的退出条件

2.实现

init 是随机给的启动值，按照上面的迭代求平均，当满足退出条件时打印 Left 或 Right 即可得到平方根。

# 二分查找法
def binary_sqrt_search(target, precision, init, max_patience=5):
    if init * init == target:
        print("精度要求: ", precision, " 目标开方数: ", target, " 平方根: ", init)
        return
    epoch = 0
    left = init
    right = target / left
    left = (left + right) / 2
    while not check_precision_state(left, right, target, precision):
        print("Epoch: ", epoch, " Left: ", right, " Right: ", left, " Dot: ", left * right)
        right = target / left
        left = (left + right) / 2
        epoch += 1

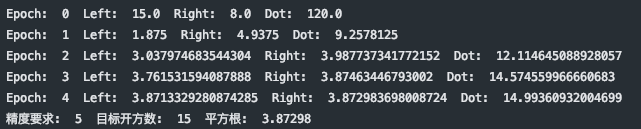
    print("精度要求: ", precision, " 目标开方数: ", target, " 平方根: ", str(left)[0: len(str(target)) + precision])

3.测试

    target_num = 15
    precision_need = 5
    init_num = 1
    binary_sqrt_search(target_num, precision_need, init_num)

可以看到每轮具体的 Left 与 Right 迭代过程，通过五轮迭代得到最终精度要求的平方根。 

四.牛顿法求对应精度平方根

1.思路

牛顿法通过导数逼近最值，本例是求目标数字的平方根，转换为数学语言是:

f(x) = x^2 - target，求 f(x) = 0 的根，f(x) 开口向上，有最小值，所以梯度下降求极值点。

导数为 : d(x) = 2 * x。

(1) 首先猜测一个初始值 init，如果 init * init = target 则直接退出，找到平方根

(2) 如果 init 不满足，则以 init - x0 为点做 f(x) 的切线，切线方程为:

           ​​                                

命令 f(x) = 0，求与 x 轴交点:

                                            

与 x 轴的交点 x1 距离极值点更近，检查 Left = x1 与 Right = target / x1 是否满足退出条件

(3) 循环上面，直到 Left , Right 达到退出条件，迭代公式为:

                                            

2.实现

根据迭代公式，不断迭代判断退出条件是否满足即可。

# 牛顿迭代
def newton_sqrt_search(target, precision, init, max_patience=5):
    if init * init == target:
        print("精度要求: ", precision, " 目标开方数: ", target_num, " 平方根: ", init)
        return

    # 原函数
    def f(x):
        return x * x - target

    # 原函数导数
    def d(x):
        return 2 * x

    epoch = 0
    while not check_precision_state(init, target / init, target, precision):
        print("Epoch: ", epoch, " Left: ", init, " Right: ", target / init, " Dot: ", target)
        init = init - f(init) / d(init)
        epoch += 1
        xn = target / init
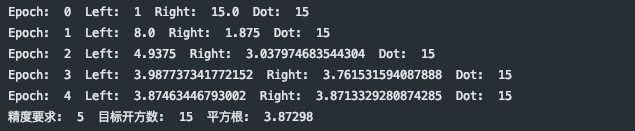
    print("精度要求: ", precision, " 目标开方数: ", target, " 平方根: ", str(init)[0: len(str(target)) + precision])

3.测试

    target_num = 15
    precision_need = 5
    init_num = 1
    newton_sqrt_search(target_num, precision_need, init_num)

可以看到每轮具体的 Left 与 Right 迭代过程，通过五轮迭代得到最终精度要求的平方根。  

五.优化

1.当 target 可完全开平方时，精度无法达到要求，造成死循环

    target_num = 100
    precision_need = 10
    init_num = 1

设置如上参数时，可以看到很快就迭代到了 Left = Right = 10.0，但是由于未满足 precision = 10 的条件，程序出现了死循环 : 

解决方案:

如果 epoch 数超过 precision 的次数，且此时 Left = Right ，则程序退出循环，以牛顿法为例:

在 xn 更新迭代后加入如下退出条件，规避 target 可完全平方的问题。

        if epoch > precision and init == xn:
            break

可以看到，当迭代次数超过 precision = 10 次后，程序判断 Left = Right，所以退出:

2.浮点数问题 Left != Right，死循环

    target_num = 12345
    precision_need = 20
    init_num = 1

Left = 111.10805551354052, Right = 111.1080555135405 ，Left 和 Right 差了一位，且未达到精度要求，无法退出。

解决方案:

增加容忍度 patience 且判断 Left = Right 时，取二者长度短的位数进行 slice 判断，以二分法为例:

首先判断 Left 和 Right 中长度较短的一方，然后截断判断是否相等，如果超过 patience 次，二者都相同则退出。

# 二分查找法
def binary_sqrt_search(target, precision, init, max_patience=5):
    patience = 0

    if init * init == target:
        print("精度要求: ", precision, " 目标开方数: ", target, " 平方根: ", init)
        return
    epoch = 0
    left = init
    right = target / left
    left = (left + right) / 2
    while not check_precision_state(left, right, target, precision):
        print("Epoch: ", epoch, " Left: ", right, " Right: ", left, " Dot: ", left * right)
        right = target / left
        left = (left + right) / 2
        epoch += 1
        min_length = min(len(str(left)), len(str(right))) - 1
        if str(left)[:min_length] == str(right)[:min_length]:
            patience += 1
        if (epoch > precision and left == right) or patience >= max_patience:
            break
    print("精度要求: ", precision, " 目标开方数: ", target, " 平方根: ", str(left)[0: len(str(target)) + precision])

 添加 patience 参数后， Left，Right 长度差一位无法判断退出条件的问题解决。

3.如何做到任意精度

这个涉及到 python 规定的精度范围，默认得到的结果为 Float，可以导入 decimal 类 , 用 Decimal 的 getcontext().prec = precision_need 方法设置精度要求:

from decimal import *
getcontext().prec = 2000


# 牛顿迭代
def newton_sqrt_search(target, precision, init, max_patience=5):
    patience = 0

    if init * init == target:
        print("精度要求: ", precision, " 目标开方数: ", target_num, " 平方根: ", init)
        return

    # 原函数
    def f(x):
        return x * x - target

    # 原函数导数
    def d(x):
        return 2 * x

    epoch = 0
    while not check_precision_state(init, target / init, target, precision):
        print("Epoch: ", epoch, " Left: ", init, " Right: ", target / init, " Dot: ", target)
        init = Decimal(init - f(init) / d(init))
        epoch += 1
        xn = Decimal(target / init)
        min_length = min(len(str(init)), len(str(xn))) - 1
        if str(init)[:min_length] == str(xn)[:min_length]:
            patience += 1
        if (epoch > precision and init == xn) or patience >= max_patience:
            break
    print("精度要求: ", precision, " 目标开方数: ", target, " 平方根: ", str(init)[0: len(str(target)) + precision])

 两个算法都可以实现更高精度的逼近，对 12345 进行 2000 位精确的开方，数字太长了显示不出来了:

平方根: 111.10805551354051124500443874307524148991137745969772997648567316178259031751676291809207065226373835669370362811742152050650995528186453651088810300374124553024886011761731936119706928213607716328092361788989764904223342054475305540092633787224004646560942854443826531523681859165166096176773670230765094187754643932637254518970747506658681177079198245672440981179498050893855412083778835772179536269865912787226226736887770282085516567638758340633473300820321594099246086766452898854997321799296242105407926600042422702964779866537973537921952376083650172033945134793274716858780884135511564112850132148422655407148218142291101513684517224422270437556094095435154019876056848969745093294641401304108394983133414915566125346078122949890551958831325614828781511458353676837009537756704098033429391740699840838775569412451022298228113560091550966876076170862807143041332095850247041769259312108574288807111674705653242060330737920108209381818739548305879663743113565743426652004744571855136228507006772406145733498118351853237611767747406558178778292230731306967632605993390293539321805996517215376379981155830282469177758892478669631147464594052272649434100797857446148046891727193477117309461563200219395107799285258064960494034119987335877271254576502459161933211014017952330819487684084628134051418156703578979451252906542217777422754551748870252141135043280329622370765451777679730896221964194232623007682129863102326247351503860685657448838869773548413565971605273601202609528430246185017523924558238246579042497383122647986137273366629480742660830392541406365688980467558686507158321740719959496950274524446974658323472228606323830318476311798442071734544768315470086450734753759423099342200930948942135874388920284680039431903516091326029356587394642736782820083546907510046598790203323143985867745196793280827830711826045530631025712089745163706938594862519724633587389754319238237434599092390214049723656667007498055664437065067316372922963414401467647987830601583899221525440336359689069622
 

六.逻辑优化-后补

闲来无事又写了一次这个题，发现判断两数精度是否达到要求时有些复杂，原始是通过对比 left 和 right 的每一位都相同，也可以通过 mid ** 2 - target <= 0.00000000001 的方法判断精度，因此程序还可以继续优化。

n = 2

import math

def sqrt(st, end):
    mid = (st + end) / 2
    if abs(math.pow(mid, 2) - n) <= 0.0000000001:
        print(mid)
        return mid
    if math.pow(mid, 2) > n:
        sqrt(st, mid)
    else:
        sqrt(mid, end)

sqrt(1, 2)

1.4142135623842478