题目描述
小 B 也是一名普及组选手,小 B 喜欢图论,尤其喜欢树。
一天,小 B 学习了递归。小 B 想要通过递归生成一棵树,因此他写下了这样的代码:
int cnt=0;
int solve(int n)
{
if(n==0){cnt++;return cnt-1;}
int ls=solve(n-1);int rs=solve(n-1);
adde(ls,rs);return ls;
}
其中 adde(x,y) 表示加入一条连接
x
,
y
x,y
x,y 的边。
可以发现,如果运行 solve(n),可以得到一棵有
2
n
2^n
2n 个点的树,这棵树的节点从
0
0
0 开始编号。小 B 在 adde 中加入了输出,并将输出重定向到了一个文件,接着调用了 solve(1e6)。显而易见地,这个文件很快变得极大,占据了整个硬盘。接着,小 B 的硬盘坏掉了。
在小 B 的电脑被送去修理的时候,小 B 无法写代码,因此小 B 决定继续思考之前调用 solve(n) 得到的树。小 B 看到了一种算法名为点分治,因此小 B 给出了
q
q
q 次询问,每次给出
x
,
d
x,d
x,d,你需要求出树上有多少个点
y
y
y 满足
x
,
y
x,y
x,y 在树上的最短路长度(经过的边数)等于
d
d
d。因为这个答案可能很大,你只需要求出这个答案对
998244353
998244353
998244353 取模的结果。
然而 x x x 也可能非常大,因此小 B 会以以下方式给出 x x x:
对于第 i i i 次询问,给出 k i k_i ki 以及 k i k_i ki 个两两不同的非负整数 v 1 , … , v k i v_1,\ldots,v_{k_i} v1,…,vki,表示 x x x 的二进制表示中所有为 1 1 1 的位为 v 1 , … , v k i v_1,\ldots,v_{k_i} v1,…,vki。
n ⩽ 1 0 7 , q ⩽ 2 × 1 0 5 , ∑ k i ⩽ 1 0 6 n\leqslant 10^7,q\leqslant 2\times 10^5,\sum k_i\leqslant 10^6 n⩽107,q⩽2×105,∑ki⩽106。
题解
首先这题不会是淀粉质(逃
观察这个图非常像树状数组,发现每个点往上爬的时候会减去 lowbit ( i ) \operatorname{lowbit}(i) lowbit(i),所以至多爬 k i k_i ki 次,我们需要设计一个 O ( ∑ k i ) \mathcal{O}(\sum k_i) O(∑ki) 的算法。每个点下满足 d = i d=i d=i 的点是满足杨辉三角的规律的。设当前节点的子树最大深度为 x x x,查询距离为 y y y(深度定义为边的个数),则这个节点下距离 y y y 的个数为 ( x y ) \dbinom{x}{y} (yx)。
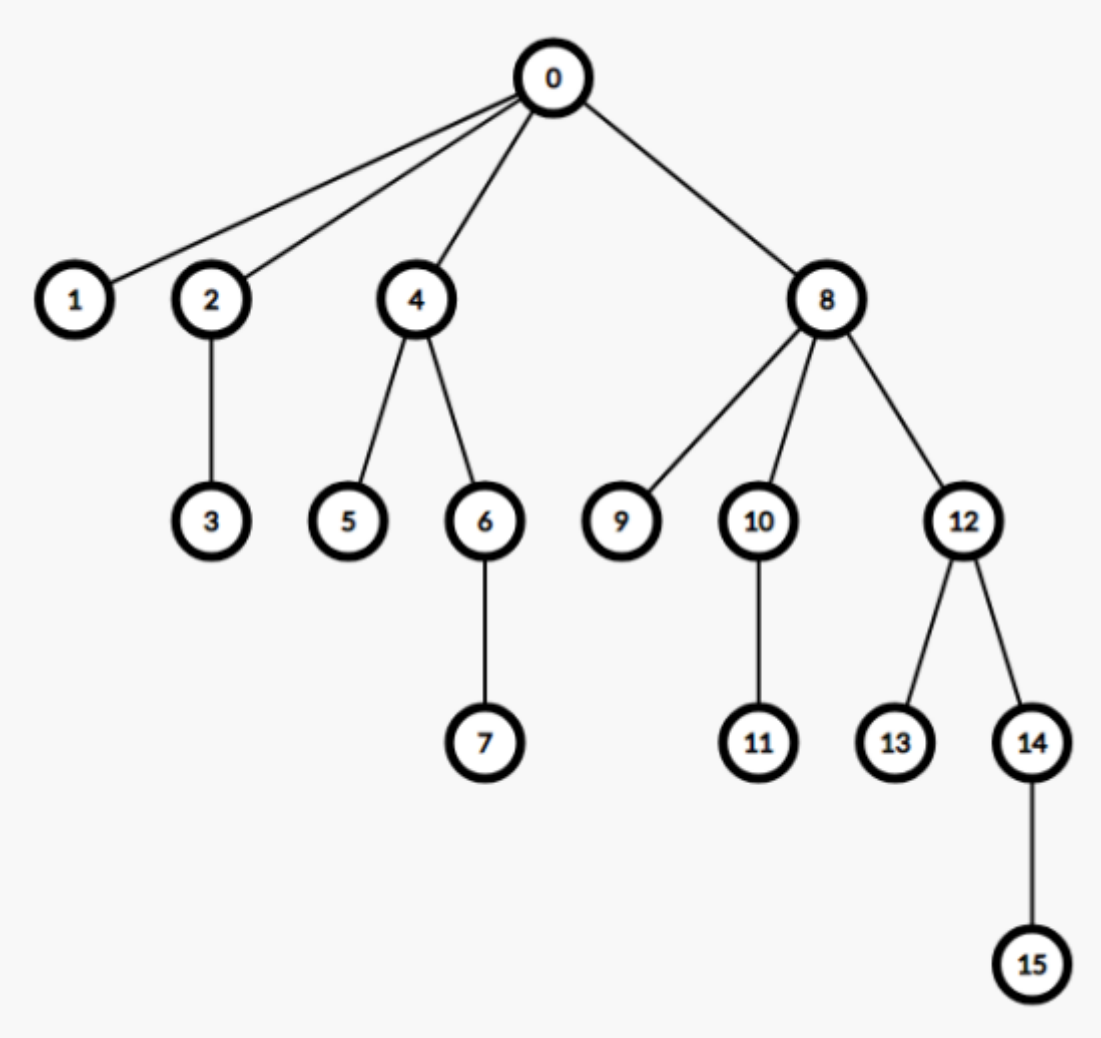
我们举两个例子 ( x = 7 , d = 3 ) (x=7,d=3) (x=7,d=3) 和 ( x = 13 , d = 4 ) (x=13,d=4) (x=13,d=4)。
当 x = 7 x=7 x=7 时,我们发现在 7 7 7 的所有子树中没有距离他为 3 3 3 的点,所以我们往上爬到 6 6 6,发现仍然没有。爬到 4 4 4 时,由于我往上爬了两层,所以我还需要距离为 1 1 1 的点,所以在点 4 4 4 中求出距离为 1 1 1 的点即为 ( 2 1 ) = 2 \dbinom{2}{1}=2 (12)=2,但是我们发现实际上满足条件的点只有 5 5 5,而没有 6 6 6,这是因为我们将一条边走了两次,不满足简单路径的性质,所以事实上我们应该减去 ( 1 0 ) = 1 \dbinom{1}{0}=1 (01)=1( 6 6 6 中子树深度为 1 1 1,我需要减去深度为 d − 2 − 1 d-2-1 d−2−1 的点,这个公式是假设我往上爬了 i i i 次,则我一定会减掉深度 d − i − 1 d-i-1 d−i−1 的点)。我们不妨继续往下看,爬到 0 0 0 时,求出 ( 4 0 ) = 1 \dbinom{4}{0}=1 (04)=1,最后得到总答案为 2 2 2。
当 x = 13 x=13 x=13 时,我们不考虑爬到 12 , 13 12,13 12,13 的情况,直接考虑 8 8 8 的情况, ( 3 2 ) = 3 \dbinom{3}{2}=3 (23)=3,将 11 , 13 , 14 11,13,14 11,13,14 都算了进来,但我们知道 12 12 12 的子树已经不可以再计算了,所以我们减去 ( 2 d − i − 1 = 1 ) = 2 \dbinom{2}{d-i-1=1}=2 (d−i−1=12)=2 个节点,得到 8 8 8 中有一个节点满足条件,以此类推,不再详述了。
所以经过我们的探索,我们会发现总答案满足(注意观察以下
i
i
i 跟上面的变化,跟数组有关的,第
i
i
i 个
v
i
v_i
vi 只爬了
i
−
1
i-1
i−1 次):
∑
i
=
1
k
(
v
i
d
−
i
+
1
)
−
(
v
i
−
1
d
−
i
)
×
[
i
≠
1
]
\sum\limits_{i=1}^k \dbinom{v_i}{d-i+1}-\dbinom{v_{i-1}}{d-i}\times [i\neq 1]
i=1∑k(d−i+1vi)−(d−ivi−1)×[i=1]
上面的公式其实不完全正确,我们需要在 v v v 数组的最后添加一个 1 1 1,表示第 n n n 位也有,这样才能计算得到从 0 0 0 出发的情况,题目没保证 v v v 单调递增,记得排序。
考虑这个算法目前的瓶颈在哪,在于处理组合数中阶乘的逆元,最大可以达到
n
!
n!
n! 的逆元,所以我们需要学习
O
(
n
)
\mathcal{O}(n)
O(n) 的阶乘逆元求法(不会只有我不会吧/kk):
inv
(
i
!
)
=
inv
[
(
i
+
1
)
!
]
×
(
i
+
1
)
\operatorname{inv}(i!)=\operatorname{inv}[(i+1)!]\times (i+1)
inv(i!)=inv[(i+1)!]×(i+1)
这样即可做到 O ( max ( n , ∑ k ) ) \mathcal{O}(\max(n,\sum k)) O(max(n,∑k)) 求值。
#include<bits/stdc++.h>
#define int long long
#define mid ((l+r)>>1)
#define fir first
#define sec second
#define lowbit(i) (i&(-i))
using namespace std;
const int N=1e7+5;
inline int read(){
char op=getchar();
int w=0,s=1;
while(op<'0'||op>'9'){
if(op=='-') s=-1;
op=getchar();
}
while(op>='0'&&op<='9'){
w=(w<<1)+(w<<3)+op-'0';
op=getchar();
}
return w*s;
}
const int mod=998244353;
int Mul(int a,int b){return (a%mod*b%mod)%mod;}
int Add(int a,int b){return (a+b)%mod;}
int Dec(int a,int b){return (a-b+mod)%mod;}
int Pow(int a,int k){
int ans=1;
while(k){
if(k&1) ans=Mul(ans,a);
a=Mul(a,a);
k>>=1;
}
return ans;
}
int inv(int x){return Pow(x,mod-2);}
int jc[N],invjc[N],x[N];
int C(int n,int m){
if(n>m||n<0||m<0) return 0;
return Mul(jc[m],Mul(invjc[n],invjc[m-n]));
}
signed main(){
int n=read(),q=read();
jc[0]=1;
invjc[0]=1;
for(register int i=1;i<=n;i++) jc[i]=Mul(jc[i-1],i);
invjc[n]=Pow(jc[n],mod-2);
for(register int i=n-1;i>=1;i--) invjc[i]=Mul(invjc[i+1],(i+1));
while(q--){
int k=read(),ans=0;
for(register int i=1;i<=k;i++) x[i]=read();
x[k+1]=n,k++;
int d=read();
sort(x+1,x+k+1);
for(register int i=1;i<=k;i++){
ans=Add(ans,C(d-i+1,x[i]));
if(i!=1) ans=Dec(ans,C(d-i,x[i-1]));
}
printf("%lld\n",ans);
}
}






















 2103
2103











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








