树形数据结构：线段树1

BasketballChick

于 2024-01-20 16:50:20 发布

阅读量953

点赞数 28

文章标签：数据结构

本文链接：https://blog.csdn.net/BasketballChick/article/details/135715538

版权

线段树，是如今维护数组常用的数据结构，其时空复杂度极优，但比较费脑子。

建树

线段树，从字面意思可以看出他是一棵树。但树怎么维护数组？

事实上，线段树是一棵二叉树，它的每个节点维护的是数组中一段区间的信息。具体解释之前，我们先看一看线段树的经典例题：

给定一个数组，要求进行单点修改操作，区间求最大值。

此时，对于数组 $a=\{1,5,6,9,2,3,1,5\}$ ，我们可以构造出线段树：

可以发现，对于一个节点，它的两个子节点就是将该节点的区间撕成两半，各自维护信息。为了复杂度正确，我们通常是将区间平分成两半。

显然，我们可以利用二叉树节点编号*2=该节点的左子节点编号和节点编号*2+1=该节点的右子节点编号将节点信息存在数组里。而线段树是一棵平衡二叉树，所以空间需要开 $4$ 倍。（具体为什么请自行思考）

下面是节点定义：

struct SegmentTree{
	int l,r;
	long long Max;
	#define l(x)t[x].l
	#define r(x)t[x].r
	#define Max(x)t[x].Max //define仅为个人习惯，也可以不加。
}t[N<<2]; //开4倍

而具体建树时，我们要用到一个重要的函数： $p u s h U p$ 。他可以在更新数据后，将叶子节点的信息往上更新。这个函数在修改操作中也会用到。

下面是 $p u s h U p$ 函数和建树的 $b u i l d$ 函数。

void pushUp(int p){
	Max(p)=max(Max(p<<1),Max(p<<1|1)); //p<<1是p的左子结点，p<<1|1是右子节点。
}
void build(int p,int l,int r){
	l(p)=l,r(p)=r;
	if(l==r){
		Max(p)=a[l];
		return;
	}
	int mid=(l+r)>>1;
	build(p<<1,l,mid),build(p<<1|1,mid+1,r);
	pushUp(p);
}
build(1,1,n) //主函数调用

这样，线段树就建好了。

更新

当我们修改 $a_x$ 时，那它会影响到树上的哪些节点呢？

事实上，如果我们将所有的节点更新一次，这就太过于浪费了——树上只会有大约 $\log n$ 个节点被修改。例如，上面那个例子中，如果 $x = 3$ ，则只有画红圈的节点会被修改：

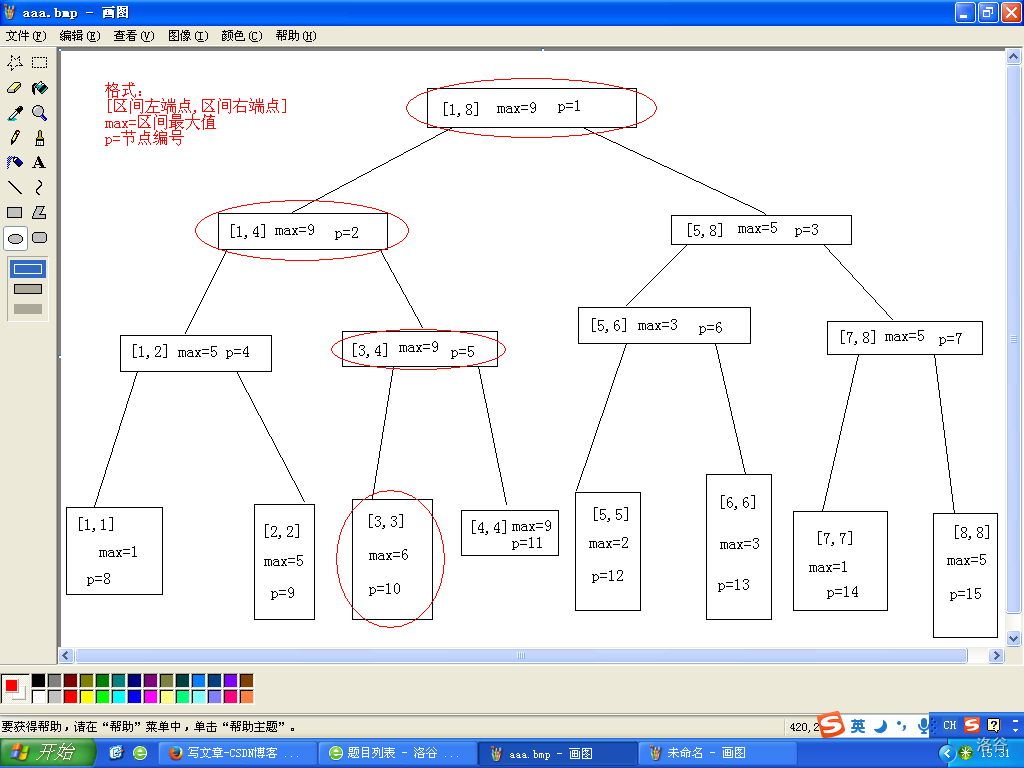
修改时，我们从根节点开始往下，每次判断：

如果 $x$ 在当前节点区间正中间或正中间的左边，则访问左子节点。
如果 $x$ 在当前节点区间正中间的右边，则访问右子节点。

到达叶子节点后，更新其数据，再通过 $p u s h U p$ 向上传递。

代码：

void update(int p,int x,long long d){
	if(l(p)==r(p)){
		Max(p)=d;
		return;
	}
	int mid=(l(p)+r(p))>>1;
	if(x<=mid)update(p<<1,x,d);
	else update(p<<1|1,x,d);
	pushUp(p);
}
update(1,x,d) //主函数调用

查询

如果没有查询操作，那前面的那些真的没有任何必要，浪费~~我大好青年的宝贵~~时间。所以重中之重还是查询。

但是我们可以像更新那样把区间内所有值一个个找出来吗？这显然是不行的，因为它的时间复杂度是 $\Theta(n \log n)$ 。

我们想想，是不是可以考虑把目标区间拆成很多段，把每一段对应一个线段树节点呢？

当然可以！

我们可以像下图一样切割 $[3, 8]$ 这个区间：

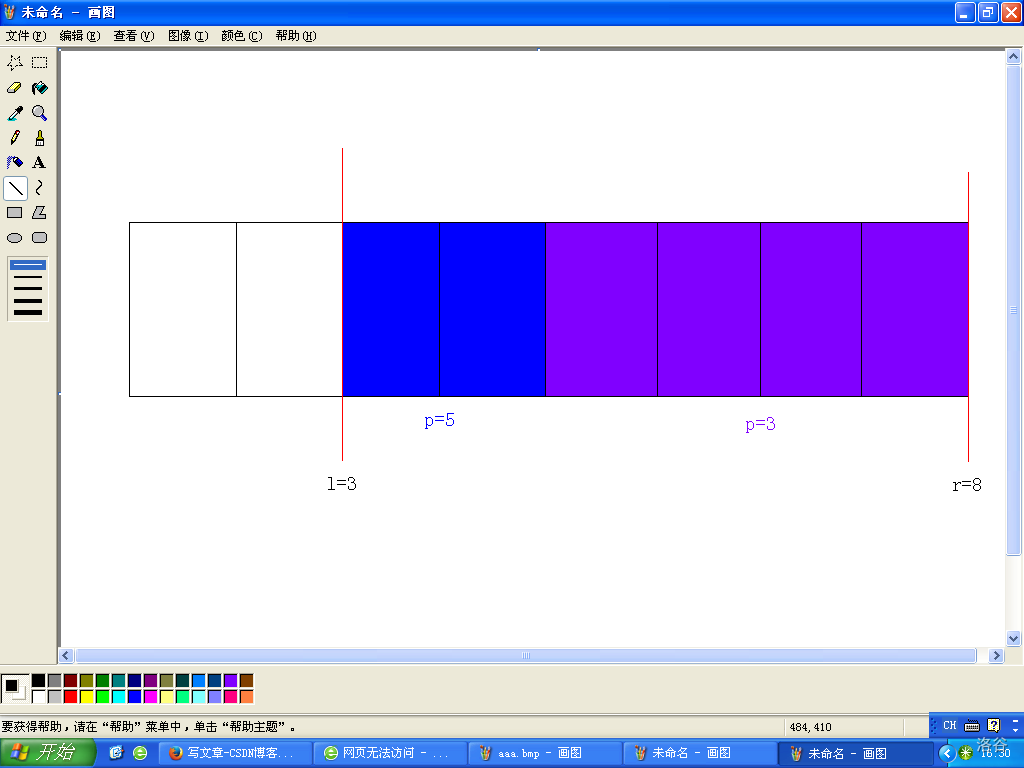
我们惊奇的发现：这不就是倍增吗？！

其实还是和倍增有一些区别的，但时间复杂度很相同，都是 $\Theta(\log n)$ 。

具体的，我们从根节点开始往下遍历：

如果目标区间包含了当前节点区间，则记录答案并返回。
如果目标区间的左节点在当前节点区间的正中间或正中间的左边，则说明其左子节点的区间与目标区间有交，访问左子节点。
如果目标区间的右节点在当前节点区间的正中间的右边，则说明其右子节点的区间与目标区间有交，访问右子节点。

注意：后两个条件有可能同时成立，千万不要加else！！！

上代码：

long long query(int p,int l,int r){
	if(l<=l(p)&&r>=r(p))return Max(p); //当前区间被目标区间包含。
	int mid=(l(p)+r(p))>>1;
	long long mx=-1e18;
	if(l<=mid)mx=max(mx,query(p<<1,l,r));
	if(r>mid)mx=max(mx,query(p<<1|1,l,r));
	return mx;
}