地理信息系统（GIS）—地理坐标系和投影坐标系

大饼酥

已于 2024-12-13 15:09:28 修改

阅读量3.7k

点赞数 38

分类专栏：地理信息系统文章标签： arcgis

于 2024-11-21 11:59:11 首次发布

本文链接：https://blog.csdn.net/BigCookies/article/details/143873770

版权

地理信息系统专栏收录该内容

1 篇文章

订阅专栏

一、简介

在地理信息系统 (GIS) 中，地理坐标系和投影坐标系是用来描述地球表面位置的两种常见方式。虽然它们都用于定位，但它们在概念和应用上有所不同。

地理坐标系是一种基于地球球面模型的坐标系统，它的核心概念是使用经纬度来定位。地理坐标系非常适合于全球定位和导航，GPS 系统就是基于地理坐标系工作的。
投影坐标系是为了在平面上准确显示地球位置而发明的，它是通过数学变换，将地球的球面坐标（经纬度）转换为平面坐标（通常是 X, Y 坐标）的一种方式。投影坐标系在工程和城市规划中非常方便，因为我们可以直接用米或公里来量距离。

二、地理坐标系

1、地球形状

真实地球不是一个正球体，而是一个两极稍扁、赤道略鼓的不规则球体。这种形状的形成是由于地球的自转和引力作用。地球的自转导致其赤道部分略微突出，而两极则因为地轴的倾斜和地球内部的物质分布不均而稍显扁平。此外，地球的扁球体形状也受到其内部构造和外部引力的共同影响。

地球这个不规则的球体到底有多不规则呢？地球的赤道半径是6378公里，两极半径是6357公里，平均半径是6371公里。赤道半径比两极半径大了21公里，北极地区高出了18.9米，南极地区则地下了24米到30米。这种形状也被称为扁球体。

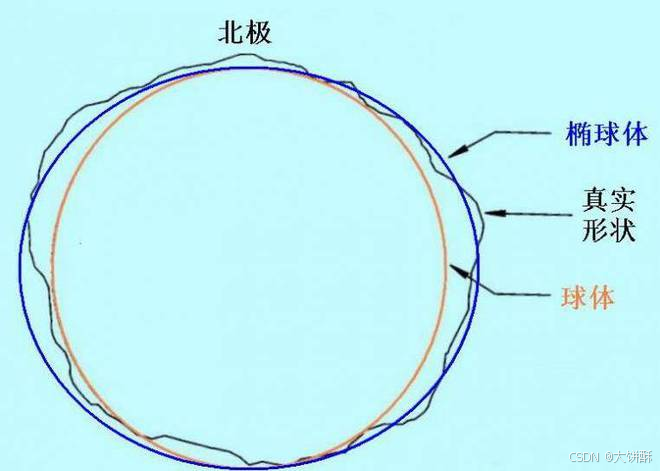
不过我个人觉得其实地球还是很圆的一个球体的。为什么呢？地球的扁率非常小，仅为0.003。地球的两极半径比赤道半径小了21公里，地球的平均半径是6371公里，只相当于地球半径的3.3‰，北极高出的18米仅相当于地球平均半径的百万分之三，南极凹进去的30米仅相当于地球平均半径的百万分之五。这么看来地球已经是非常的完美的球体了。

2、地球的三级逼近

地球表面有海洋、平原、丘陵、高山等起伏形态，是一个不规则曲面。这样的曲面无法用数学公式进行表达，不能作为制图和测量的基准，所以为了达到我们用数学进行表达的目的，就得对真实的地球进行建模，进行逼近，从而引入了地球三级逼近的概念。

2.1、一级逼近—大地水准面

大地水准面是地球的第一级逼近。假设当海水处于完全静止的平衡状态时，从海平面延伸到所有大陆下部，而与地球重力方向处处正交的一个连续、闭合的曲面，这就是大地水准面，但是还是无法直接用数学公式表达出来。

2.2、二级逼近—椭球体

大地水准面可以近似成一个规则椭球体，但并不是完全规则，其形状接近一个扁率极小的椭圆绕短轴旋转所形成的规则椭球体，这个椭球体称为地球椭球体，简称椭球体。椭球体是地球的第二级逼近，如下图红色示意，它是一个规则的数学表面，所以人们视其为地球体的数学表面，用于测量计算的基准面。
目前比较广泛的椭球体是1984年定义的世界大地坐标系（WGS84）使用的椭球体，使用的长半径、短半径分别为6378137m和6356752.3m，扁率为1：298.26。

2.3、三级逼近—大地基准面

地球椭球体表面和地球表面肯定不是完全贴合，因而即使使用同一个椭球面，不同的地区由于关心的位置不同，当需要最大限度的贴合自己关心的区域表面时，就需要一个椭球曲面来描述这个最大贴合表面，这个表面就是大地基准面，也是地球表面的第三级逼近，而这个大地基准面所在的椭球体就是「参考椭球体」，参考椭球体可以当做是根据大地基准面的位置偏移、偏转而来。
地球椭球体与大地基准面是一对多的关系，也就是说基准面是在地球椭球体基础上建立的，但椭球体不能代表基准面，同样的椭球体可以定义多个基准面。
为了让大地基准面与当地更匹配，测量和定位更精确，很多国家都开发自己的大地基准面。WGS1984基准面采用WGS84椭球体，它是一地心坐标系，即以地心作为椭球体中心，目前GPS测量数据多以WGS1984为基准。我们通常称谓的北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面。

2.4、大地坐标系

大地坐标系根据其原点的位置不同，分为地心坐标系和参心坐标系。

地心大地坐标系：椭球体的原点与地球质心（基准面）重合，WGS84、CGCS2000
参心大地坐标系：椭球体的原点不与地球质心（基准面）重合，Beijing-54、Xian-80

3、模拟地球逼近流程

3.1、地球

3.2、做出来大地水准面

3.3、依据大地水准面，生成椭球体

3.4、在椭球体上考虑高程信息，并赋予了x、y、z轴，变成了基准面，中间绿色点为基准面质心

3.5、为了更好的拟合地球，且不过于复杂，以然选择椭球体模拟地球，但是这个时候椭球体基于基准面进行一定的移动。红色点椭球体中心，绿色点基准面质心

3.6、红点与绿色点重合，则为地心大地坐标系

3.7、加入我们比较看重基准面红色的这块区域，想让基准面与椭球体更合的贴合，我们对椭球体移动，这个时候红色、绿色点不重合了，则为参心大地坐标系

4、地理坐标系参数

地理坐标系是由纬度、经度和相对于地面的高度所组成的三维球面坐标系

地理坐标系的基点/线

经线：地球自转轴的两端分别为北天极和南天极，穿过北天极和南天极的大圆被称为经线，也叫子午线。
本处子午线：即0度经线，大部分坐标系指通过英国格林尼治旧天文台的经线。
纬线：平行于赤道线，赤道线是0度纬线。

地理坐标系的三维

纬度φ：赤道面与过P点和地心的直线所组成的夹角。
经度λ：经过P点的经线和0度经线（本初子午线之间）的夹角。
高度h：即P点相对于椭球体的垂直距离。

三、投影坐标系

1、投影坐标系的由来

虽然地理坐标系在定位上很有优势，但它并不适合直接用于平面地图绘制。地球是一个近似球体的曲面，而我们要在平面（比如纸张或计算机屏幕）上展示地图，这样直接把球面上的位置投影到平面上会造成比例失真，特别是在高纬度地区，面积和形状都会发生明显的变形。这时，我们就需要使用投影坐标系。

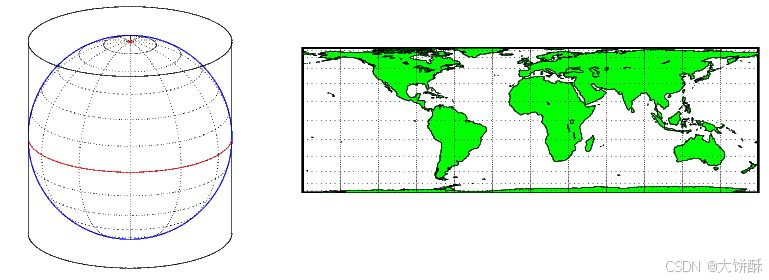
先来看看我们平时最常见的世界地图是长这样的。

我们很容易联想到这样一个图形是无法平整的贴在一个球体表面的。真正要帖在球体表面的地图是下图这样的，而且即便如此，也只是近似平整而已。

由于地球是一个近似球体，地球表面是一个不可展开面，因此将地球表面展开后必然会出现撕裂和褶皱。将三维的地球表面映射到二维平面的过程就是地图的投影。而由于空间维度的降低，在投影的过程中，地图的扭曲和形变是无法避免的，因此，在绘制世界地图时，面积、方向和距离是无法全部顾及到。

2、投影分类

投影可以分为三大类：

按变形分类有等角投影、等面积投影、任意投影。
按投影面可分为圆锥投影、圆柱投影、方位投影。
按投影角度分为正轴投影、斜轴投影、横轴投影。

三个特征排列组合，就形成了常见了一些投影，如墨卡托投影。

3、常见的投影方式

3.1、等差分纬线多圆锥投影

下面的世界地图采用的投影方式叫做等差分纬线多圆锥投影。我国于1963年按照地图投影反求法设计的一种任意多圆锥投影。该投影广泛用于我国出版的小比例尺世界地图。

该投影中纬线为对称于赤道的同轴圆圆弧，圆心位于中央经线上。中央经线为一直线，其它经线为对称于中央经线的曲线，且离中央经线越远，其经线间隔成比例地递减；极点表示为圆弧，其长度为赤道投影长度的二分之一，经纬网的图形有球形感。
我国被配置在地图中接近于中央的位置，保持太平洋完整。由于该投影的性质是接近等面积的任意投影，因此我国绝大部分地区面积变形小。在中学使用的世界地图中的世界的气候类型和洋流图、世界政区图和自然带的分布图都是采用的这种投影图。

上图显示了等差分纬线多圆锥投影投影形变的程度，图中的1.0线表示面积形变为0，大于1.0表示图上面积比起实际面积放大了，小于1.0表示图上面积比起实际面积缩小了。我国之所以普遍采用这种投影方式也有一部分原因是我国大部分国土面积都处于低形变程度的地图中。

此外，使用这种投影还存在的问题是：即使是在实际中互相垂直的方向，在地图中却表现为非垂直。例如上图中的经线和纬线。

3.2、等角度投影—墨卡托投影

为了真实表示地图中的方向，就得提到大名鼎鼎的墨卡托投影（Mercator Projection），其投影出的世界地图如下图所示，经线纬线互相垂直并且方向正确。墨卡托投影被广泛应用例如谷歌地图等地图场景。

墨卡托投影是正轴等角圆柱投影，是由地理学家墨卡托于16世纪发明的。墨卡托投影的绘制方式是将一张纸卷成圆筒状包住地球，纸面接触地球赤道，模拟地球球心为光源，将地球表面轮廓照射到圆筒上从而形成的地图。在赤道上，由于地球和纸面接触，因此投影出的面积和方向也是完全真实的。然而，离开赤道往南北级方向可以明显发现，投影出的图案面积发生了形变。由于光源在球心，因此南极点和北极点将不会出现在投影中，甚至两级的极圈也不会被投影在地图中。

假设R为赤道半径，r为北纬60度纬线的半径。r/R=sin(90-60)=0.5，周长=2*pi*半径，因此赤道的半径是北纬60度的2倍。然而，在墨卡托投影的世界地图里，北纬六十度和赤道是一样长的。因此为了保持大陆的形状，在北纬六十度，地图的南北方向也被拉长了2倍。因此，在墨卡托投影的地图中，高纬度的地区会被放大许多。这种放大有多夸张呢，这里给大家展示动图感受一下。

俄罗斯靠近两极面积拉伸严重
俄罗斯的面积大约为 1709.82 万平方公里，非洲的总面积为 3022.1532 万平方公里。

利用数据比较俄罗斯和非洲大小
由此可见，现在从地图上直观地看到各个国家的面积大小，其实是严重失真的。

在这里介绍给大家一个基于 Mercator projection的地图拼图游戏，大家可以从中体会下地图拉伸的感觉。链接地址，大家可以试下：Compare Countries With This Simple Tool

3.3、等面积投影

等面积投影的全称是：正球在正轴的圆柱上进行等面积投影，简称等积圆柱投影。其特点是，通过等积投影出的地图上，每个国家的面积不失真（但是形状会失真），比如下面这个世界地图：

从图中可以感受到非洲有多大，南极洲有多小，而常用的等角圆柱投影（Mercator投影）中，非洲小的可怜，南极大到离谱，所以说，等积投影能正确的展示每个主权国家的战略纵深。绘制方式很简单，想象地球卡在一个等高的圆柱中，圆柱的高等于球的直径，然后沿平行于赤道平面的方向投影，如下图：

3.4、等距离投影—麦卡托投影

等距离圆柱投影是公认的所有地图投影里，数学变换最简单的一种。麦卡托投影在高纬度地区为了保持形状的准确而将纬线之间的距离拉长；等距离圆锥投影的所有相邻经线和纬线之间的距离都是一样的。因此，在南北方向上，地图上任意两点的距离是保持精确的。这种地图缺点很多，既不保持形状的准确，也不保证面积的准确。但因为它制作简单，因此很多时候它被用作索引地图（例如世界各国列表）或示意地图（例如时区、货币分布、国际组织成员分布等地图）的投影。

3.5、折衷投影—罗宾逊投影

罗宾逊投影中，形状、面积和角度等都做不到精确，然而它们之间进行了互相的妥协。和麦卡托地图相比，它的陆地轮廓形状发生了可以接受的扭曲，而高纬度地区的面积变化虽然还存在，但也变小了不少。这种投影方法被发明后，很快就被用于绘制各种各样的世界地图了。
罗宾森投影可能是一种最常用于绘制世界地图的折衷伪圆柱地图投影。“国家地理”将罗宾森投影用于其世界地图约十年，直到 1998 年。