博弈论-棋类游戏三择一定理的证明

rain melon

已于 2024-11-23 20:24:01 修改

阅读量1.6k

点赞数 29

分类专栏：博弈论文章标签：笔记

于 2024-11-23 20:23:09 首次发布

本文链接：https://blog.csdn.net/Bilibili_TIAN/article/details/143953079

版权

博弈论专栏收录该内容

1 篇文章

订阅专栏

写在前面：本专栏是为了应付博弈论期末考试所做的一个记录，旨在督促自己使用规范化流程和语言去对数学定理进行证明、对数学问题进行求解，如有不当之处，请广大网友批评指正。

证明参考与来源：《博弈论》-Michael Maschler

棋类游戏的三择一定理：

要说明这个问题，首先要定义规则明确的棋类游戏的博弈模型。

首先明确规则：

国际象棋博弈有两个参与人，传统上称之为白棋和黑棋，在比赛的开始，每个参与人在棋盘上都有16枚棋子，每个棋子都有自身的行进规则，白棋先走，黑棋后走，双方轮流走棋，一次走一步棋，一局国际象棋有以下三个可能的结果：

白棋胜，条件是白棋将死黑棋的王，同时白棋自己的王没有被吃掉
黑棋胜，条件是黑棋将死白棋的王，同时黑棋自己的王没有被吃掉
黑白双方平局。

平局的判定条件：

轮到黑棋走棋，黑王没有被将军，但却没有合法的移动。
轮到白棋走棋，白王没有被将军，但同样没有合法的移动。
黑白双方同意达成平局。
棋面（board position）已经排除双方胜利的可能（双方都无法将死对方的王）。
双方在连续50个回合内都没有吃掉对方任何一子，并且未移动兵，轮走一方宣布和棋。
相同的棋面出现三次。

随后定义数学符号语言：

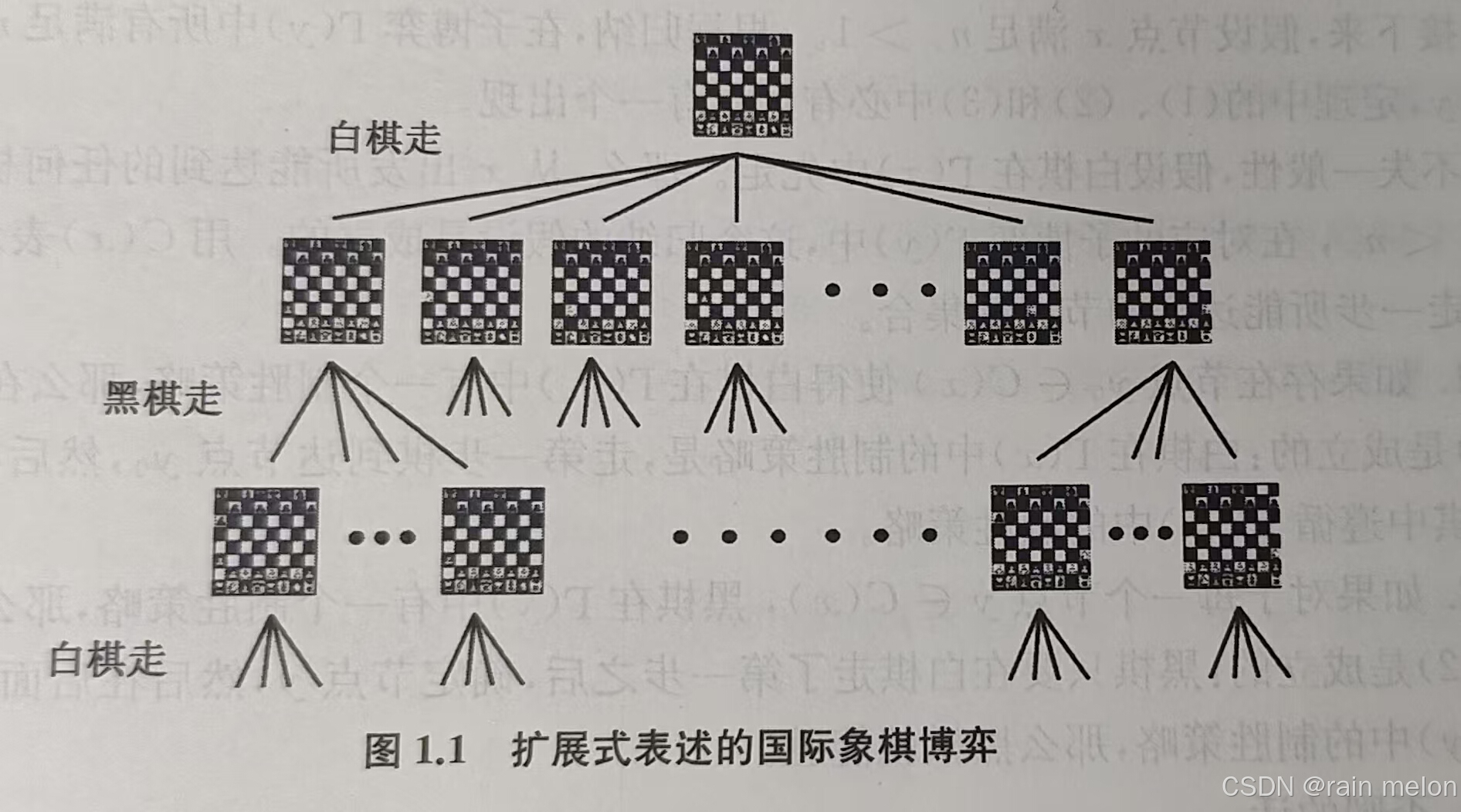
棋面（board position）：白黑双方每一颗棋子的身份和在棋盘上的位置。

棋局态势（game situation）：将白黑双方每一回合产生的棋面记录下来，形成的一个序列。

棋面集合无法完整记录棋局的运转，仅仅是所有可能的列举，而棋局态势作为棋面的时间步序列，可以完整记录一个棋局。

我们用X来表示所有可能出现的棋面的集合，某一个棋面用x∈X来表示。

所有棋局态势的集合用H来表示，某一个棋局态势用α∈H来表示，其中

$\alpha =\left ( x_{0}, x_{1},..., x_{m} ,...,x_{n} \right ),n\in N,x_{m}\in X,1\leqslant m\leqslant n$

这里的m意为“中间步”，n意为最后的终结步。

一个棋局态势α必须满足的条件是：

${x_{0}}$ 必须是开局棋面；（也就是必须是规则规定的初始的棋面）
对于任意一个偶数整数m，棋面 ${x_{m}}$ 到 ${x_{m+1}}$ 是通过白方的一步合法移动得到的；
对于任意一个奇数整数m，棋面 ${x_{m}}$ 到 ${x_{m+1}}$ 是通过黑方的一步合法移动得到的；

策略的描述和定义：

白方策略： $S_{w}:H_{even}\rightarrow X$

要求棋面 ${x_{n}}$ 到 ${x_{n +1}}$ 是通过白方的一步合法移动得到的,所有白方策略的集合用 ${\Omega_{w}}$ 表示。

$S_{w}\left ( \alpha \right )=x_{n+1},\alpha =\left ( x_{0} ,...,x_{n}\right ),n\equiv 0(mod 2))$

黑方策略： $S_{b}:H_{odd}\rightarrow X$

要求棋面 ${x_{n}}$ 到 ${x_{n +1}}$ 是通过黑方的一步合法移动得到的,所有白方策略的集合用 ${\Omega_{b}}$ 表示。

$S_{b}\left ( \alpha \right )=x_{n+1},\alpha =\left ( x_{0} ,...,x_{n}\right ),n\equiv 1(mod 2))$

三择一定理的内容：

棋类游戏，有且只有以下一种情况成立：

白方有必胜策略
黑方有必胜策略
白黑双方有至少平局策略

证明方法：符号逻辑

首先定义符号

X是一个有限集合；
$A\left ( x \right )$ 是X上的抽象逻辑公式；
∀表示任取，∃表示存在，¬表示取反。

博弈树（game tree）：棋局态势集合H可以形象化为树形图，某一个棋局态势α∈H称之为博弈树的顶点（vertices）。

根顶点（root vertex）: $\alpha =\left ( x_{0} \right )\in H$ 称之为顶点。

顶点的子顶点（Children vertices of a vertex）：∀α∈H

顶点的后代顶点（Descendant vertices of a vertex）：∀α∈H

叶子（leaf）：博弈完成时候的棋局态势。（注意：必须是棋局分出胜负后的最后的终局才能称作“叶子”）

从顶点α开始的子博弈树（subgame beginning at α）：∀α∈H，子博弈Γ(α)是以α为根顶点，结合其后代顶点构成的子树。

一般用 $n_{\alpha }$ 来表示子博弈中的顶点数量。

“子”为“儿子”，后代则为“孙，重孙......”，但“子”也算作后代。

接下来开始证明：

主要思路是对子博弈Γ(α)顶点的数量进行归纳。

STEP1：

假设α是满足 $n_{\alpha }$ =1的顶点，那么可以得到α是终局态势（叶子），此时有三种结果：

白方胜-此时∅为白方制胜策略
黑方胜-此时∅为黑方制胜策略
黑白平局-此时双方至少平局策略为∅

那么α满足三择一定理。

继续讨论

STEP2：

假设α是满足 $n_{\alpha }$ >1的顶点，由归纳法，满足 $n_{\beta }$ < $n_{\alpha }$ 的所有子博弈Γ(β)都满足三择一定理。

不妨设白棋在子博弈Γ(α)中先手，那么从α出发所能达到的任何棋面β都满足 $n_{\beta }$ < $n_{\alpha }$ ，在对应的子博弈Γ(β)中

$\forall \beta \in C\left ( \alpha \right ),n_{\beta }< n_{\alpha }$

STEP3：

讨论：

1.如果存在 $\beta_{0}\in C\left ( \alpha \right )$ 使得白方在子博弈Γ( $\beta _{0}$ )中有一个必胜策略 $S_{w}$ ，那么白方在博弈Γ(α)中有必胜策略，此时2成立与否1均成立。

$\alpha \rightarrow \beta _{0}\rightarrow S_{w}$

2.如果任意 $\beta_{}\in C\left ( \alpha \right )$ 使得黑方在子博弈Γ( $\beta _{}$ )中有一个必胜策略 $S_{b}$ ，那么黑方在博弈Γ(α)中有必胜策略

$\alpha \rightarrow \beta _{}\rightarrow S_{b}$

3.讨论

若1不成立，如果任意 $\beta_{}\in C\left ( \alpha \right )$ 都无法使得白方在子博弈Γ( $\beta _{}$ )中有一个必胜策略，那么黑方在这个子博弈中有必胜策略，或者白黑双方有至少平局策略。

若2不成立，存在 $\beta_{0}\in C\left ( \alpha \right )$ 使得黑方在子博弈Γ( $\beta _{0}$ )中没有必胜策略，此时讨论1成立的情况没有意义，若1不成立，此时白方没有必胜策略，双方均无法必胜，此时白黑双方在子博弈Γ( $\beta _{0}$ )有至少平局策略 $\left ( S_{w},S_{b} \right )$ 。

因此，在3中的几种情形中白黑双方在子博弈Γ(α)中均存在至少平局策略。

证毕。